1.8 The Output

The result of all this is a model with two giant probability functions. In this section I’ll talk through what those functions look like with a worked example, and then some graphs about how well the models perform at their intended task.

The worked example involves David Makinson’s article “The Paradox of the Preface” (Makinson 1965). The input to the model looks like this.

Table 1.1: Words in “The Paradox of the Preface.”
Word	Word Count
rational	14
beliefs	11
paradox	9
book	8
author	7
belief	6
statements	6
believes	5
errors	5
incompatible	5
preface	5
present	5
set	5
true	5
believe	4
example	4
however	4
logically	4
maciver	4

That is, the word rational appears fourteen times, beliefs appears eleven times, and so on. This is a list of all of the words in the article, excluding the various stop words described above and the words that appear one to three times.

The model gives a probability to the article being in each of ninety topics. For this article, as for most articles, it just gives a residual probability to the vast majority of topics. For eighty-three topics, the probability it gives to the article being in that topic is about 0.0003. The seven topics it gives a serious probability to are:

Table 1.2: Topic Probabilities for “The Paradox of the Preface.”
Topic	Probability
76	0.2681
4	0.2668
15	0.1311
81	0.1266
59	0.1109
37	0.0385
39	0.0318

I’m going to spend a lot of time in the next chapter on what these topics are. For now, I’ll just refer to them by number.

The model also gives a probability to each word turning up in a paradigm article for each of the topics. For those nineteen words that the model saw as input, we can look at how frequently the model thinks a word should turn up in each of these seven topics.

Table 1.3: Word frequencies for topics in “The Paradox of the Preface.”
Word	Topic 4	Topic 15	Topic 37	Topic 39	Topic 59	Topic 76	Topic 81
present	0.0029	0.0018	0.0019	0.076	0.00047	0.00033	0.00062
rational	8.3e-12	9.6e-20	3e-11	2.7e-34	9.1e-32	0.0029	0.044
true	0.0011	0.016	1.3e-05	0.0056	0.14	0.015	0.00081
however	0.0035	0.0044	0.0031	0.0028	0.0027	0.0032	0.0026
statements	1.7e-43	0.088	3.1e-26	1.3e-33	2.2e-12	1.5e-44	4.5e-59
example	0.00039	0.0028	0.0058	0.0011	0.0024	0.0033	0.0024
believes	3.3e-33	2.5e-26	2.2e-44	9.4e-25	1.2e-18	0.011	0.0018
set	0.00077	0.001	0.058	2.4e-08	1.7e-06	0.00094	0.0014
believe	0.00075	2.8e-05	3.3e-17	0.00082	8.1e-09	0.045	0.0032
maciver	6.4e-05	2.3e-10	1.1e-156	9.5e-72	3.8e-66	1.4e-34	1.1e-150
book	0.02	7.8e-07	1.1e-19	5.8e-22	1.3e-18	4.3e-10	0.00022
incompatible	1.6e-31	0.00084	6.4e-05	0.00051	5e-13	7.6e-05	0.00018
beliefs	1.2e-39	1.1e-44	1.2e-48	3.4e-35	2.4e-26	0.077	0.0035
author	0.0092	1.2e-23	2.8e-21	4.5e-31	2.2e-11	3.6e-09	2.4e-14
belief	1.1e-25	3.3e-27	1.4e-42	4e-30	3.4e-23	0.13	1.1e-10
errors	0.00022	9.7e-23	1.9e-30	9.2e-38	5.2e-35	5.7e-06	3.2e-27
logically	1.8e-38	0.018	0.0012	0.00026	4e-09	9.6e-10	8.2e-15
preface	0.00069	2e-33	8.6e-63	3e-105	4.8e-07	1.5e-06	2.2e-11
paradox	1.1e-31	1.2e-09	0.0014	4.8e-13	0.02	9.5e-12	2.4e-26

But the model doesn’t think that “The Paradox of the Preface” is a paradigm case of any one of these topics; it thinks it is a mix of seven. Therefore, what it thinks the word frequencies in that article should be can be worked out by taking weighted means of these columns, with the weights given by the topic probabilities. And that gives the following results:

Table 1.4: Measured and modeled frequencies for “The Paradox of the Preface.”
Word	Wordcount	Measured Frequency	Modeled Frequency
rational	14	0.1207	0.0065
beliefs	11	0.0948	0.0217
paradox	9	0.0776	0.0023
book	8	0.0690	0.0055
author	7	0.0603	0.0025
belief	6	0.0517	0.0358
statements	6	0.0517	0.0118
believes	5	0.0431	0.0033
errors	5	0.0431	0.0001
incompatible	5	0.0431	0.0002
preface	5	0.0431	0.0002
present	5	0.0431	0.0038
set	5	0.0431	0.0031
true	5	0.0431	0.0228
believe	4	0.0345	0.0130
example	4	0.0345	0.0022
however	4	0.0345	0.0033
logically	4	0.0345	0.0025
maciver	4	0.0345	0.0000

The modeled frequency of rational is given by multiplying, across seven topics, the probability of the article being in that topic, by the expected frequency of the word given it is in that topic. And the same goes for the other words. What I’m giving here as the measured frequency of a word is not its frequency in the original article; it is its frequency among the words that survive the various filters I described above. In general that will be two to three times as large as its original frequency.

The aim is that the two columns here would line up. And, of course they don’t. In fact, the model doesn’t end up doing very well with this article; it is still a long way from equilibrium.

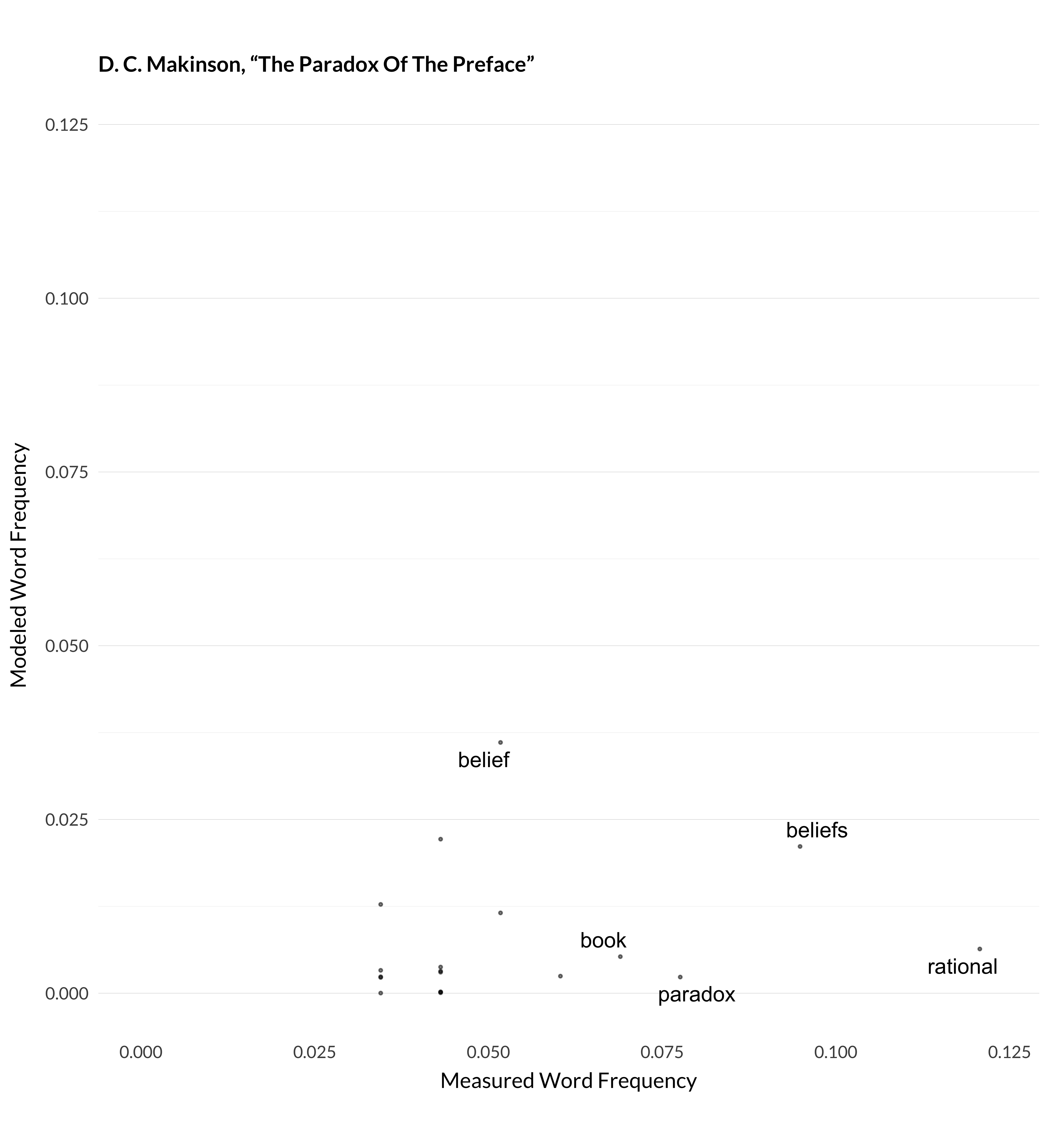
A scatterplot where the x axis shows how often each word appears in D. C. Makinson, 1965, “The Paradox of the Preface,” Analysis 25:205–7., and the y axis shows how often the model anticipated that word to appear. Here the expectations are rarely met. The words rational, beliefs, belief, paradox, book are highlighted. Each of them is well below the forty-five degree line. That means they appear in the article more often than the model expects. The word belief only appears a bit more often than expected, then others appear much more often.

Figure 1.1: Modeled and measured frequency for Makinson (1965).

On that graph, every dot is a word type. The x axis represents the frequency of that word type in the article (after excluding the stop words and so on), and the y axis represents how frequently the model thinks the word ‘should’ appear, given its classification of the article into ninety topics, and the frequency of words in those topics. Ideally, all the dots would be on the forty-five degree line coming northeast out of the origin. Obviously, that doesn’t happen. It can’t really, because, to a very rough approximation, I’ve only given the model ninety degrees of freedom, and I’ve asked it to approximate over 32,000 data points.

Actually, this is one of the least impressive jobs the model does. I measured the correlations between measured and modeled word frequency, i.e., what this graph represents, for six hundred highly cited articles. Among those six hundred, this was the twenty-third lowest correlation between measured and modeled frequency. But in many cases, that correlation was very strong. For example, here are the graphs for three more articles where the model manages to understand what’s happening.

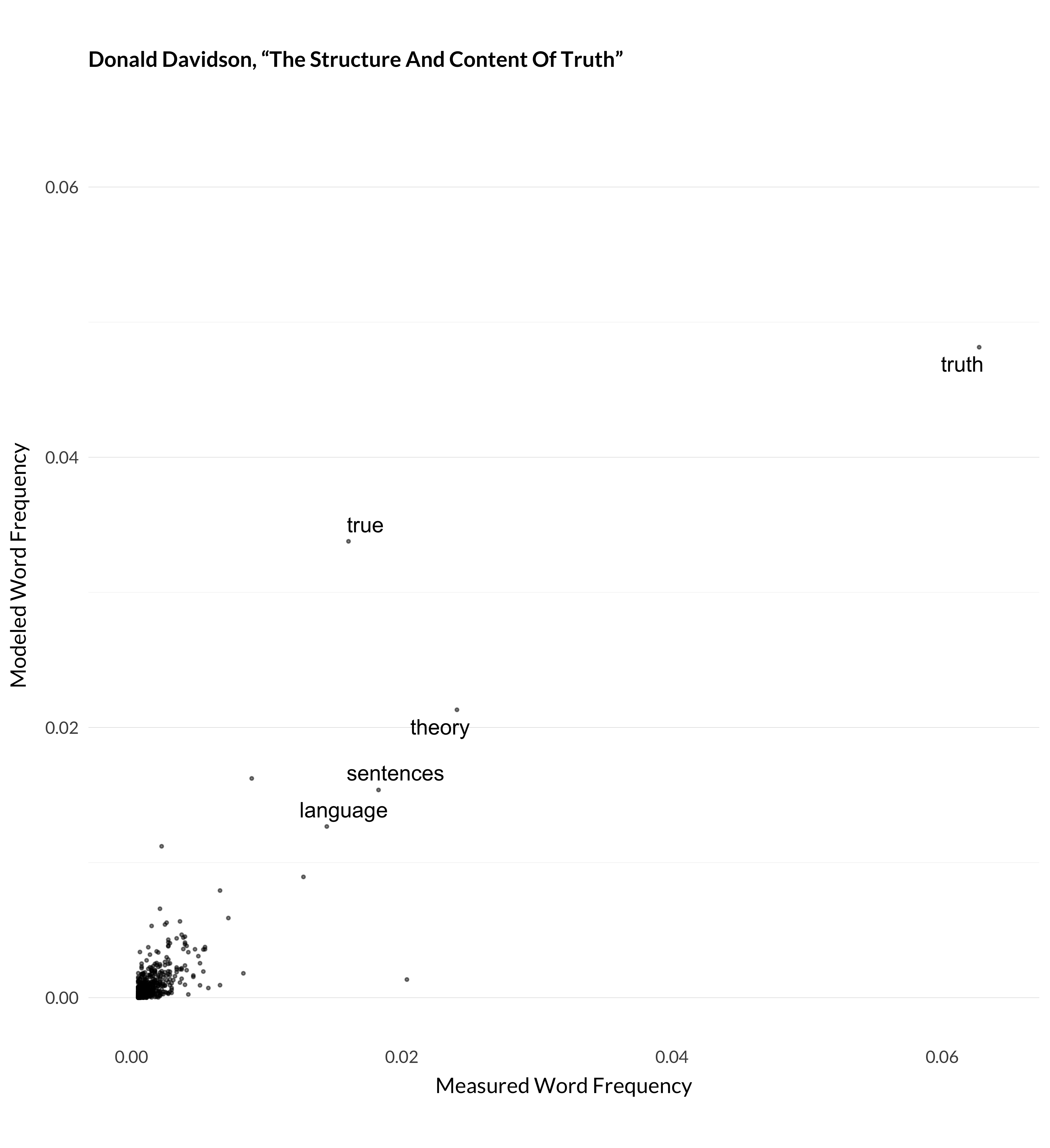
A scatterplot where the x axis shows how often each word appears in Donald Davidson, 1990, “The Structure and Content of Truth,” Journal of Philosophy 87:279–328., and the y axis shows how often the model anticipated that word to appear. Here the expectations are usually met. The words truth, true, theory, sentences, language are highlighted. Each of them is close to the forty-five degree line. That means they appear in the article about as often than the model expects. The word truth appears a lot; it is 6% of the words in the article. The model expects a little less; around 5%. The others are very close to the forty-five degree line.

Figure 1.2: Modeled and measured frequency for Davidson (1990).

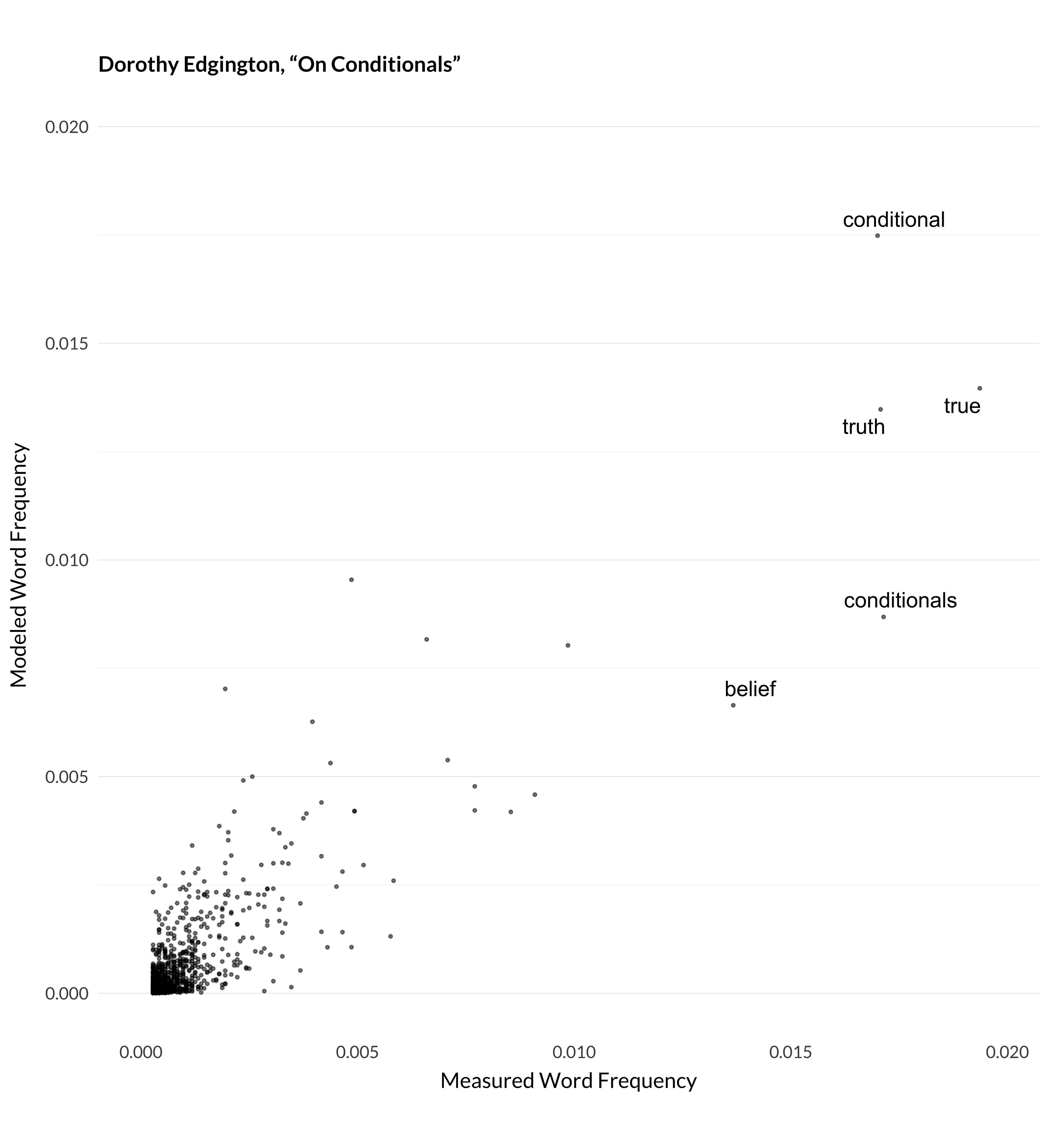
A scatterplot where the x axis shows how often each word appears in Dorothy Edgington, 1995, “On Conditionals,” Mind 104:235–329., and the y axis shows how often the model anticipated that word to appear. Here the expectations are usually met. The words conditional, true, truth, conditionals, belief are highlighted. Each of them is close to the forty-five degree line. That means they appear in the article about as often than the model expects.

Figure 1.3: Modeled and measured frequency for Edgington (1995).

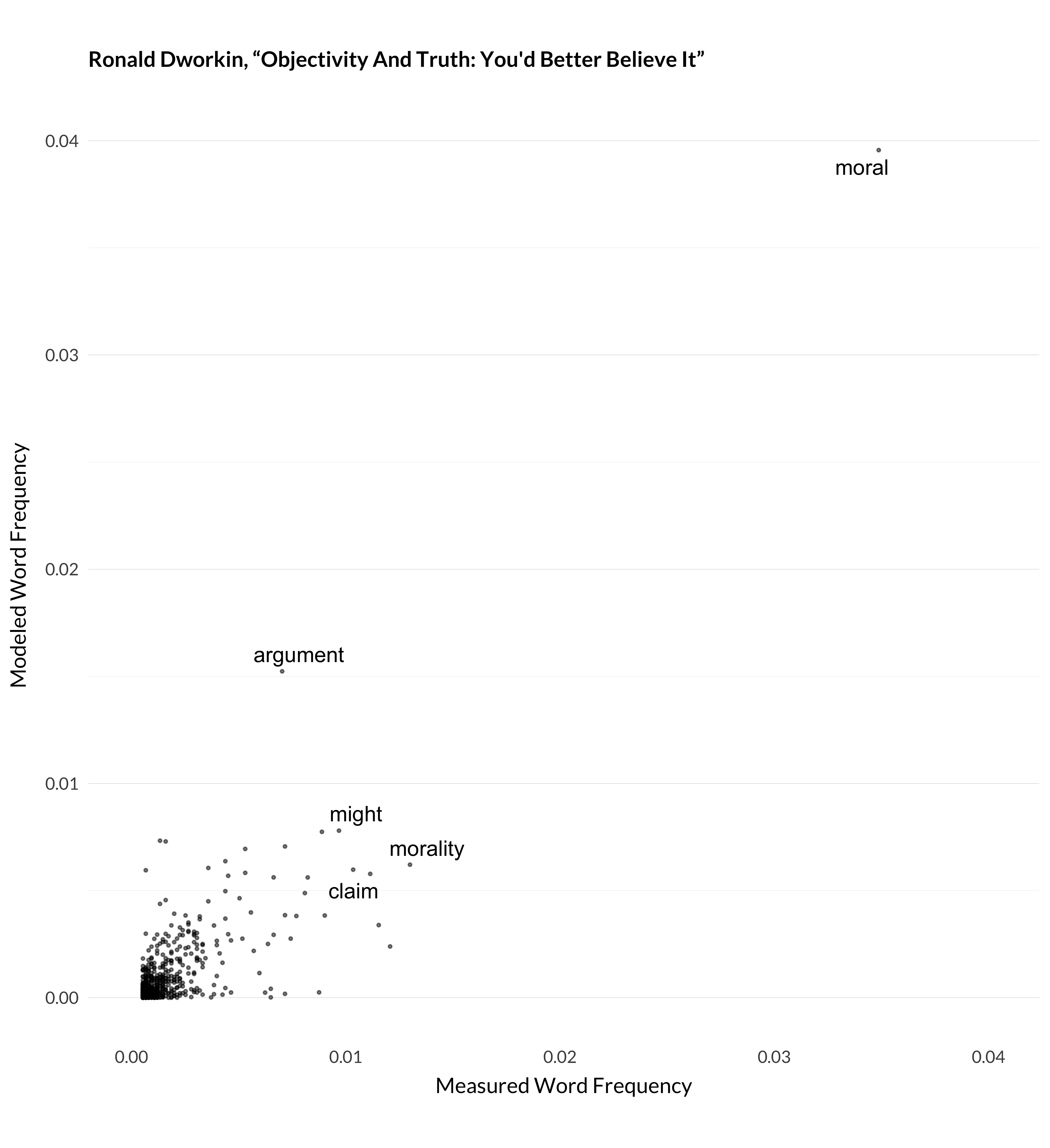
A scatterplot where the x axis shows how often each word appears in Ronald Dworkin, 1996, “Objectivity and Truth: You'd Better Believe It,” Philosophy and Public Affairs 25:87–139., and the y axis shows how often the model anticipated that word to appear. Here the expectations are usually met. The words moral, argument, morality, might, claim are highlighted. Each of them is close to the forty-five degree line. That means they appear in the article about as often than the model expects. The word moral appears a lot, about 4% of all words in the article. And the model predicts this correctly.

Figure 1.4: Modeled and measured frequency for Dworkin (1996).

There are some articles that it doesn’t manage as well—typically articles with unusual words. (It also does poorly with short articles, like “The Paradox of the Preface”.)

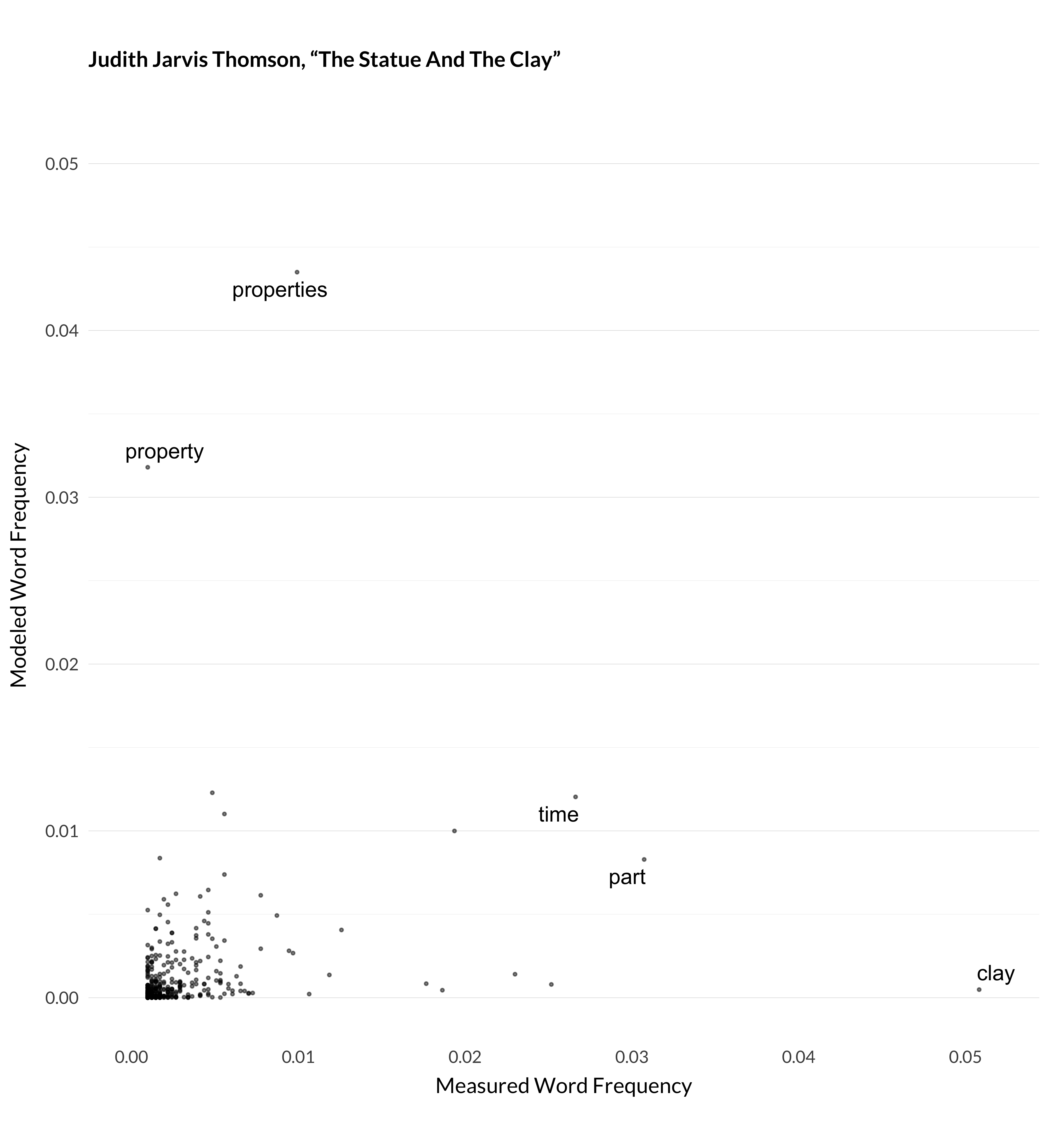
A scatterplot where the x axis shows how often each word appears in Judith Jarvis Thomson, 1998, “The Statue and the Clay,” Noûs 32:149–73., and the y axis shows how often the model anticipated that word to appear. Here the expectations are rarely met. The words properties, clay, part, time, property are highlighted. Each of them is far from the forty-five degree line. The model expects the words property and properties will appear a lot, 3-4% of the time, but they make up only about 1% of the words. It does not expect the words time, part and, especially, clay, to appear as often as they do.

Figure 1.5: Modeled and measured frequency for Thomson (1998).

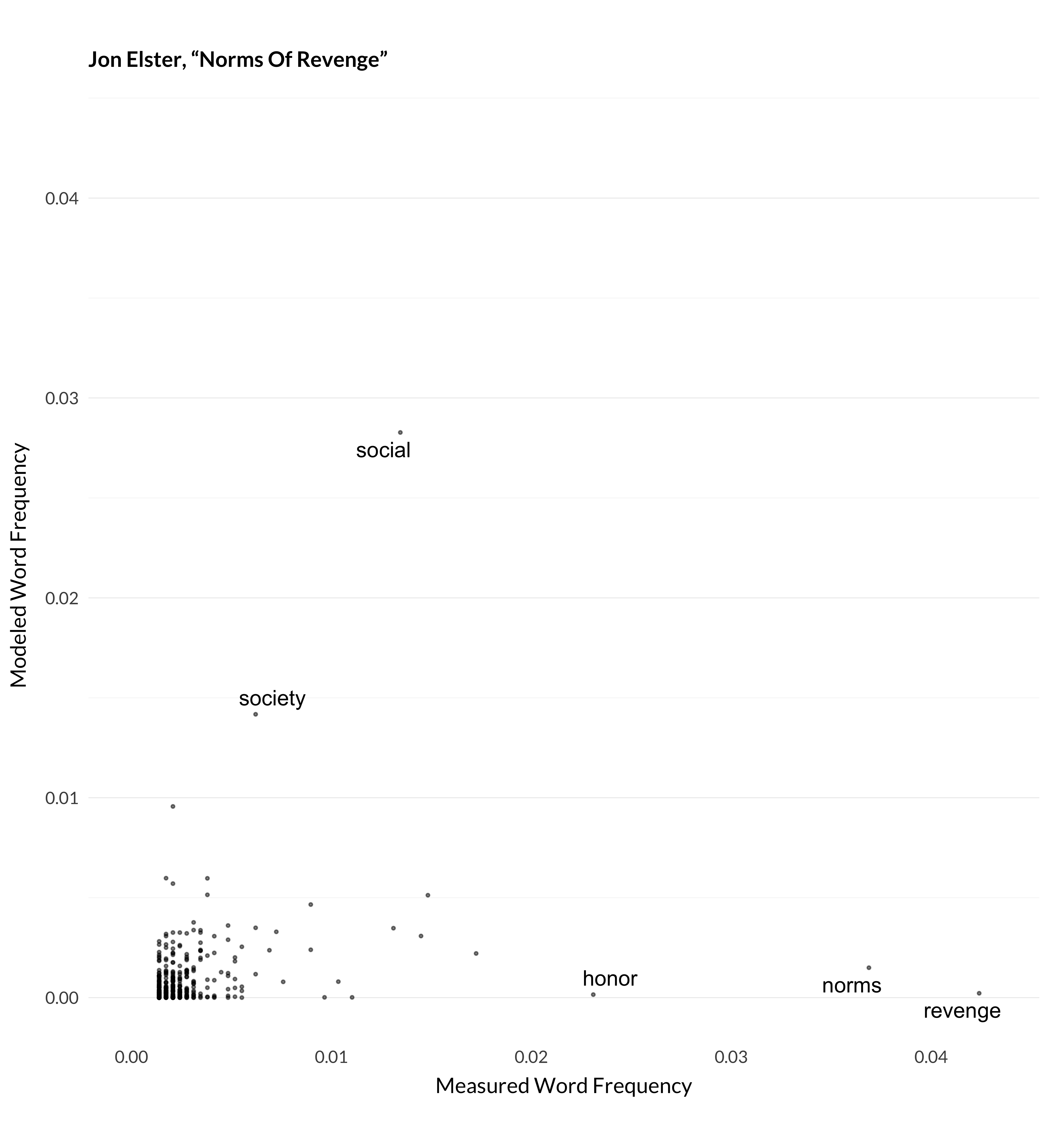
A scatterplot where the x axis shows how often each word appears in Jon Elster, 1990, “Norms of Revenge,” Ethics 100:862–85., and the y axis shows how often the model anticipated that word to appear. Here the expectations are rarely met. The words revenge, social, norms, honor, society are highlighted. Each of them is far from the forty-five degree line. The model expects the words society and social to appear more often than they do. But it is very surprised at how often the words honor, norms, and revenge, appear.

Figure 1.6: Modeled and measured frequency for Elster (1990).

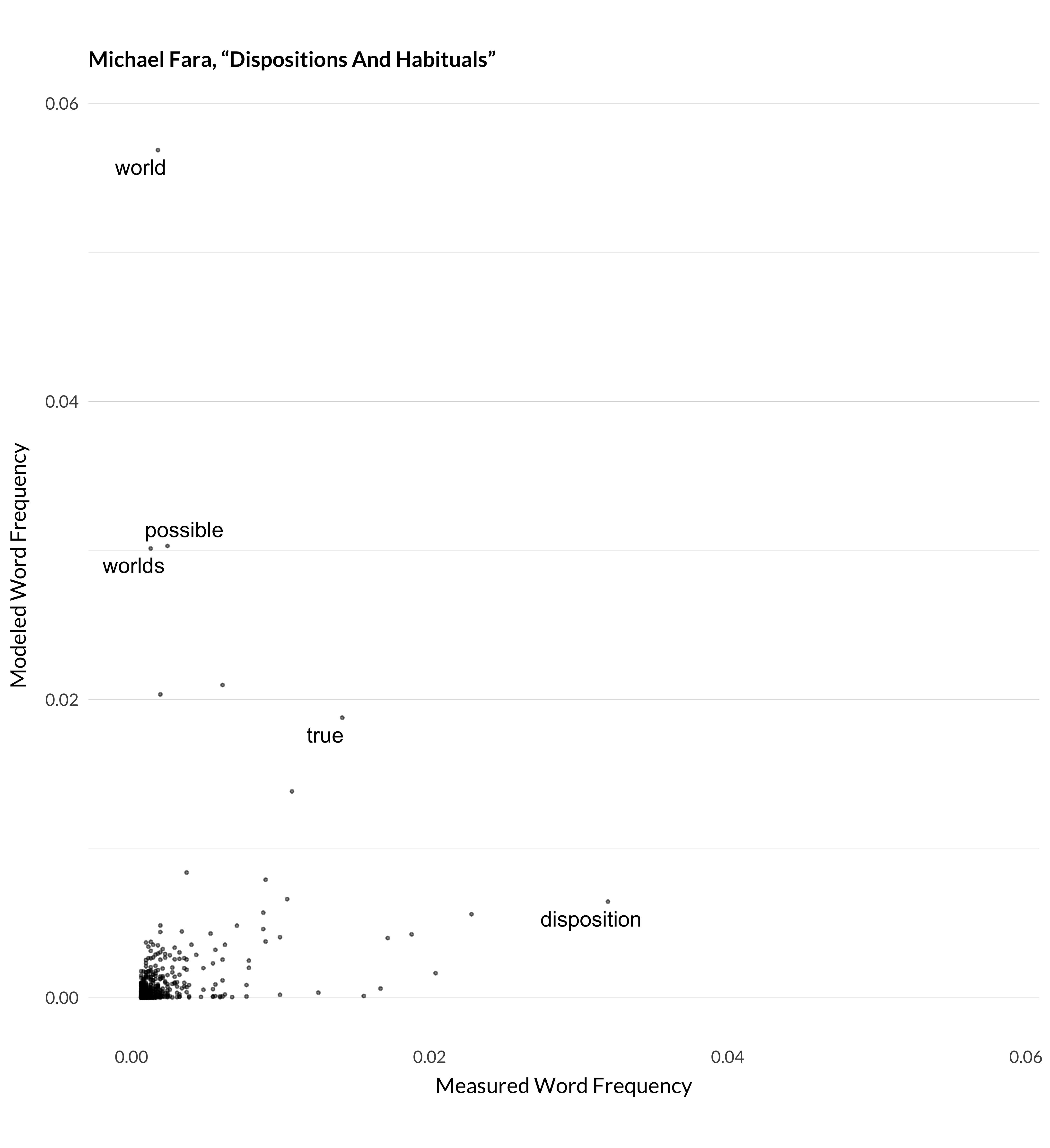
A scatterplot where the x axis shows how often each word appears in Michael Fara, 2005, “Dispositions and Habituals,” Noûs 39:43–82., and the y axis shows how often the model anticipated that word to appear. Here the expectations are rarely met. The words world, disposition, true, possible, worlds are highlighted. Four of them are far from the forty-five degree line. The model expects the words possible, worlds and, especially, world, to appear much more often than they do. But it expects the word disposition to appear much less. The model does correctly predict that the word true will appear about 2% of the time.

Figure 1.7: Modeled and measured frequency for Fara (2005).

A few different things are going on here. In Elster’s article, the model doesn’t expect any philosophy article to use the word revenge as much as the author does. In Fara’s article, the model lumps articles about modality (especially possible worlds) in with articles on dispositions. (This ends up being topic 80.) And so it expected that Fara will talk about worlds, given he is also talking about dispositions, but he doesn’t. Thomson’s article has both of these features. The model is surprised that anyone is talking about clay so much. And it expects that a metaphysics article like Thomson’s will talk about properties more than Thomson does.

It isn’t perfect, but as seen above, it does pretty well with some cases. The papers I’ve shown so far are pretty much outliers though; here are some more typical examples:

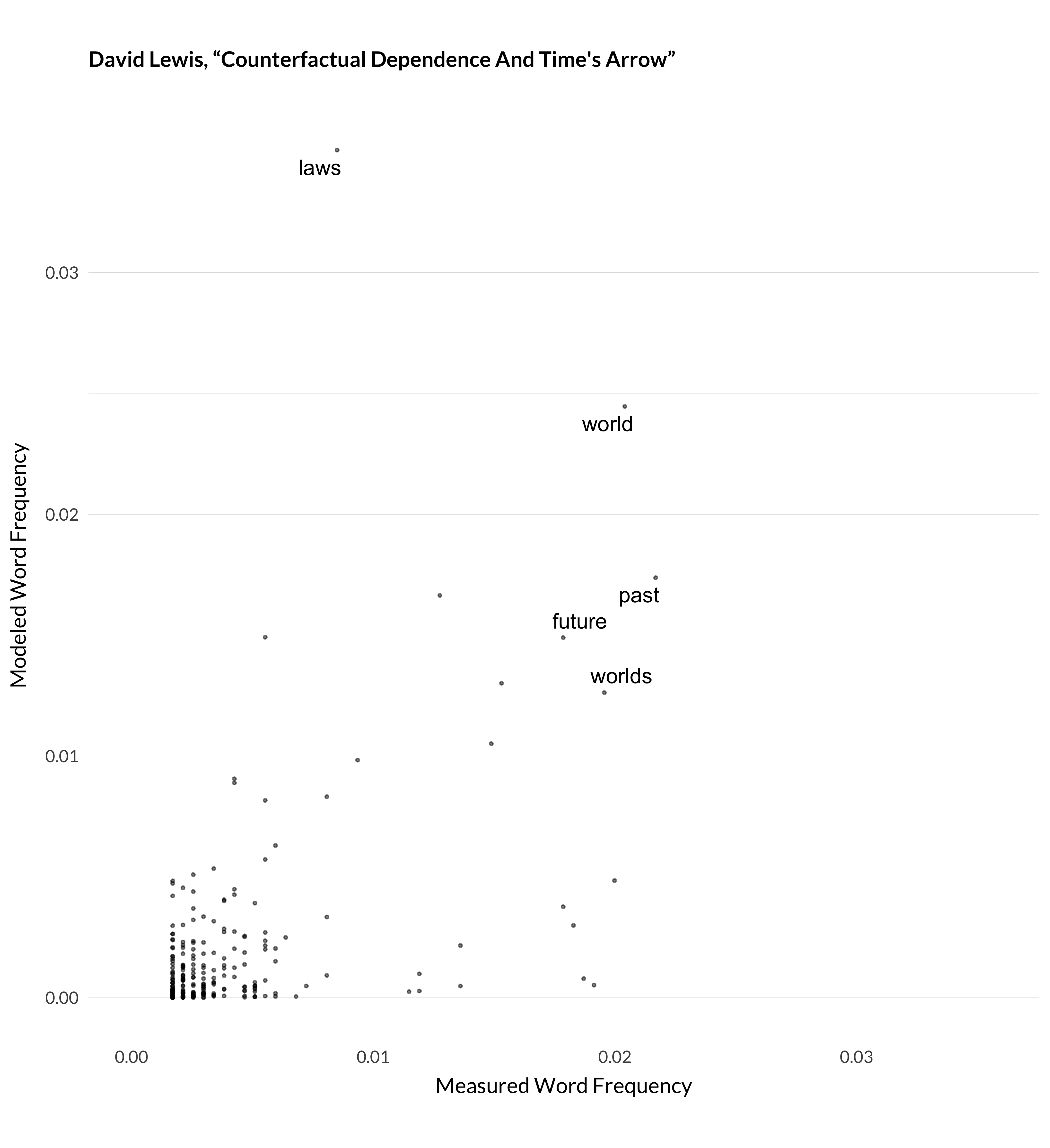
A scatterplot where the x axis shows how often each word appears in David Lewis, 1979, “Counterfactual Dependence and Time's Arrow,” Noûs 13:455–76., and the y axis shows how often the model anticipated that word to appear. Here the expectations are mostly met. The words world, laws, past, future, worlds are highlighted. Four of them are close to the forty-five degree line. But the model expects the word laws to appear much more often than it does.

Figure 1.8: Modeled and measured frequency for Lewis (1979).

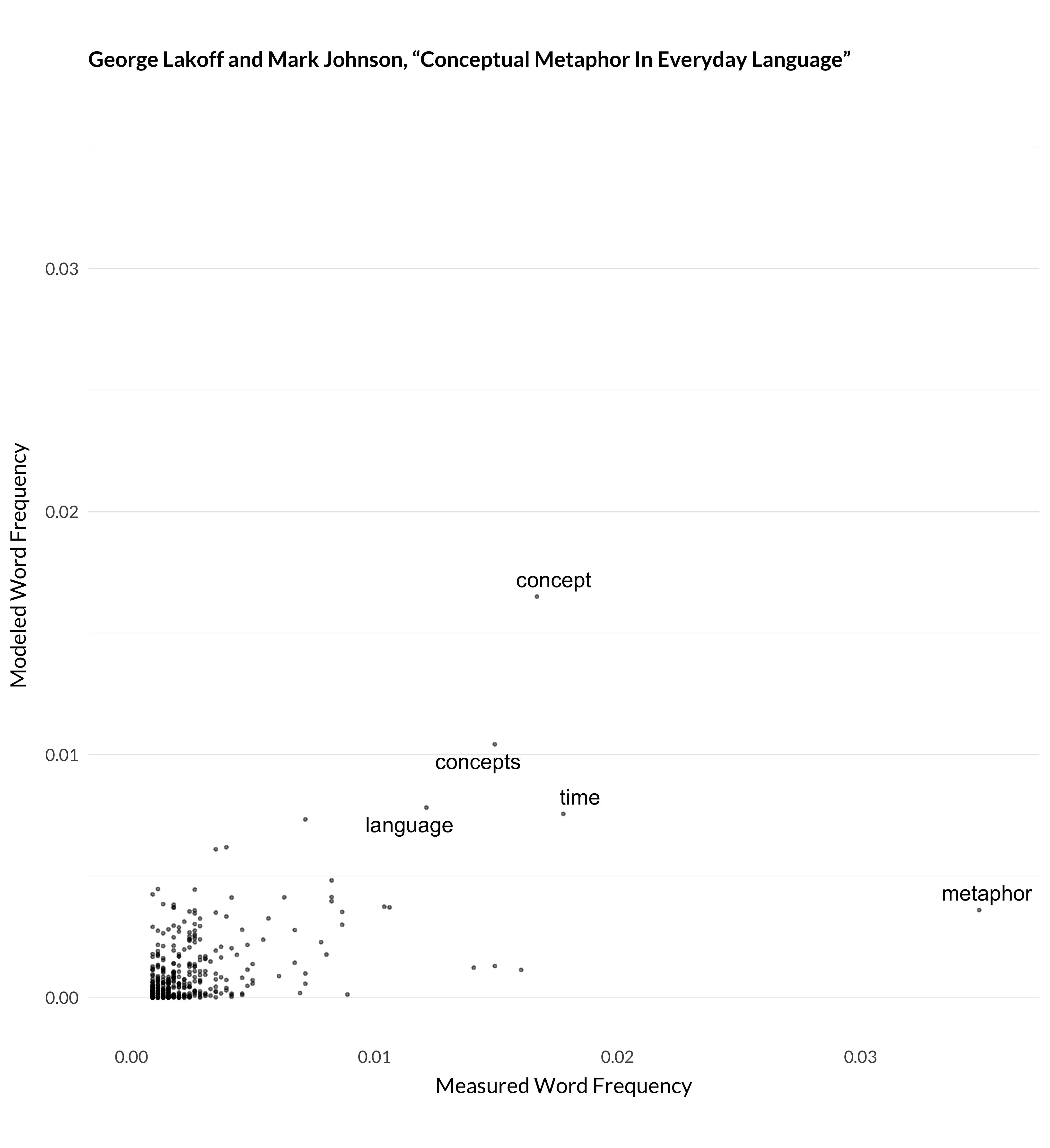
A scatterplot where the x axis shows how often each word appears in George Lakoff and Mark Johnson, 1980, “Conceptual Metaphor in Everyday Language,” Journal of Philosophy 77:453–86., and the y axis shows how often the model anticipated that word to appear. Here the expectations are mostly met. The words metaphor, concept, concepts, time, language are highlighted. Four of them are close to the forty-five degree line. That means they appear in the article about as often than the model expects. But the model does not expect the word metaphor to appear so often.

Figure 1.9: Modeled and measured frequency for Lakoff and Johnson (1980).

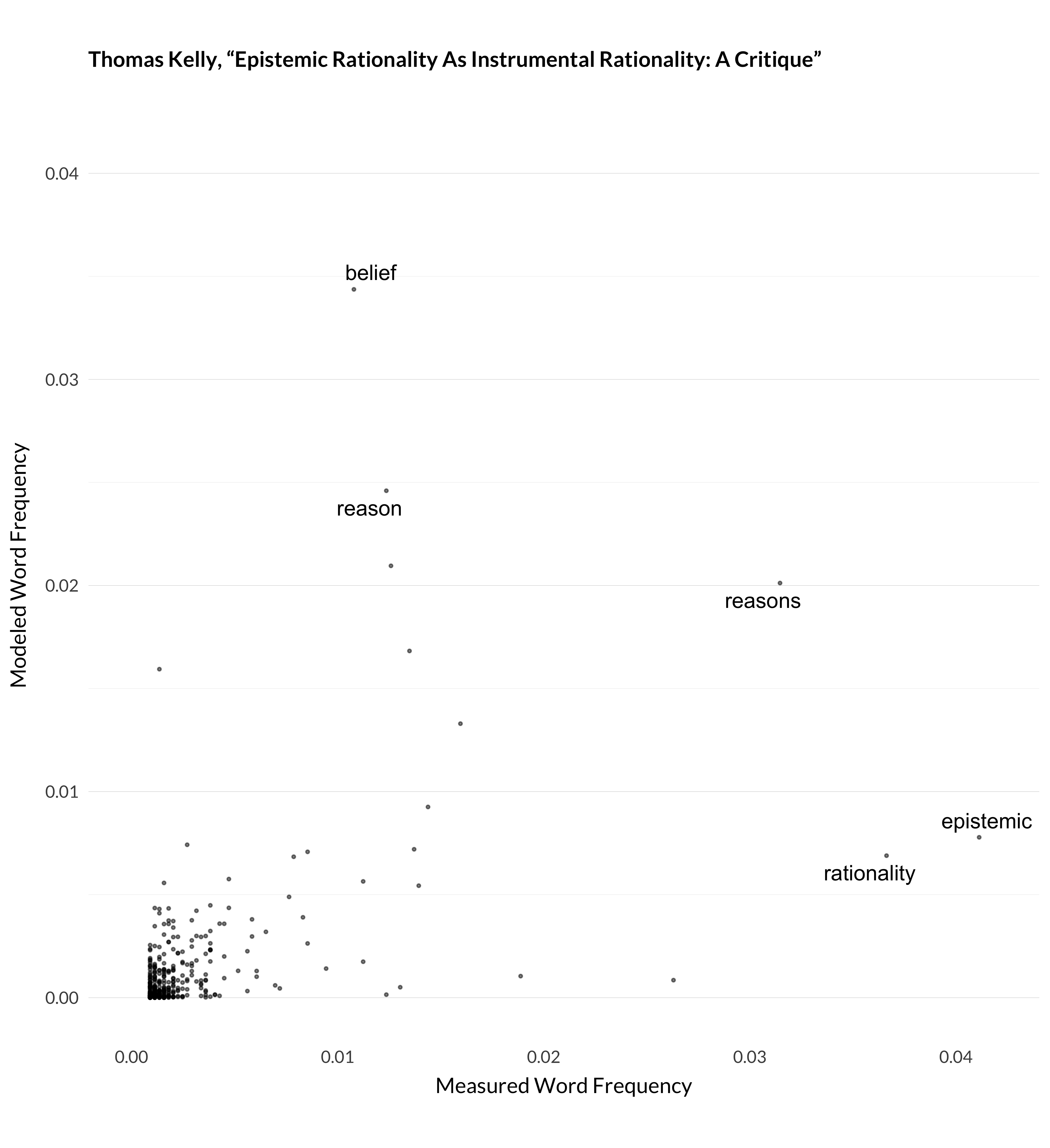
A scatterplot where the x axis shows how often each word appears in Thomas Kelly, 2003, “Epistemic Rationality as Instrumental Rationality: A Critique,” Philosophy and Phenomenological Research 66:612–40., and the y axis shows how often the model anticipated that word to appear. Here the expectations are rarely met. The words reasons, epistemic, belief, rationality, reason are highlighted. Belief and reason are far above the forty-five degree line, epistemic and rationality far below it. The model expects the word reasons to make up 2% of the words in the article, and in fact it makes up 3%.

Figure 1.10: Modeled and measured frequency for Kelly (2003).

It’s not perfect, but the general picture is that the model does a pretty good job of modeling 32000 articles given the tools it has. And, more importantly from the perspective of this book, the way it models them ends up grouping like articles together. And that’s what I’ll use for describing trends in the journals over their first 138 years.