2.37 Sets and Grue
Category: Philosophy of Science/Logic and Mathematics
Keywords: member, sets, classes, axiom, ordered, satisfies, ordering, pairs, formula, assignment, goodman, class, constants, null, theorem
Number of Articles: 555
Percentage of Total: 1.7%
Rank: 9th
Weighted Number of Articles: 532.9
Percentage of Total: 1.7%
Rank: 10th
Mean Publication Year: 1973.8
Weighted Mean Publication Year: 1976.2
Median Publication Year: 1974
Modal Publication Year: 1974
Topic with Most Overlap: Truth (0.0375)
Topic this Overlaps Most With: Mathematics (0.0422)
Topic with Least Overlap: Emotions (0.00035)
Topic this Overlaps Least With: History and Culture (0.00119)
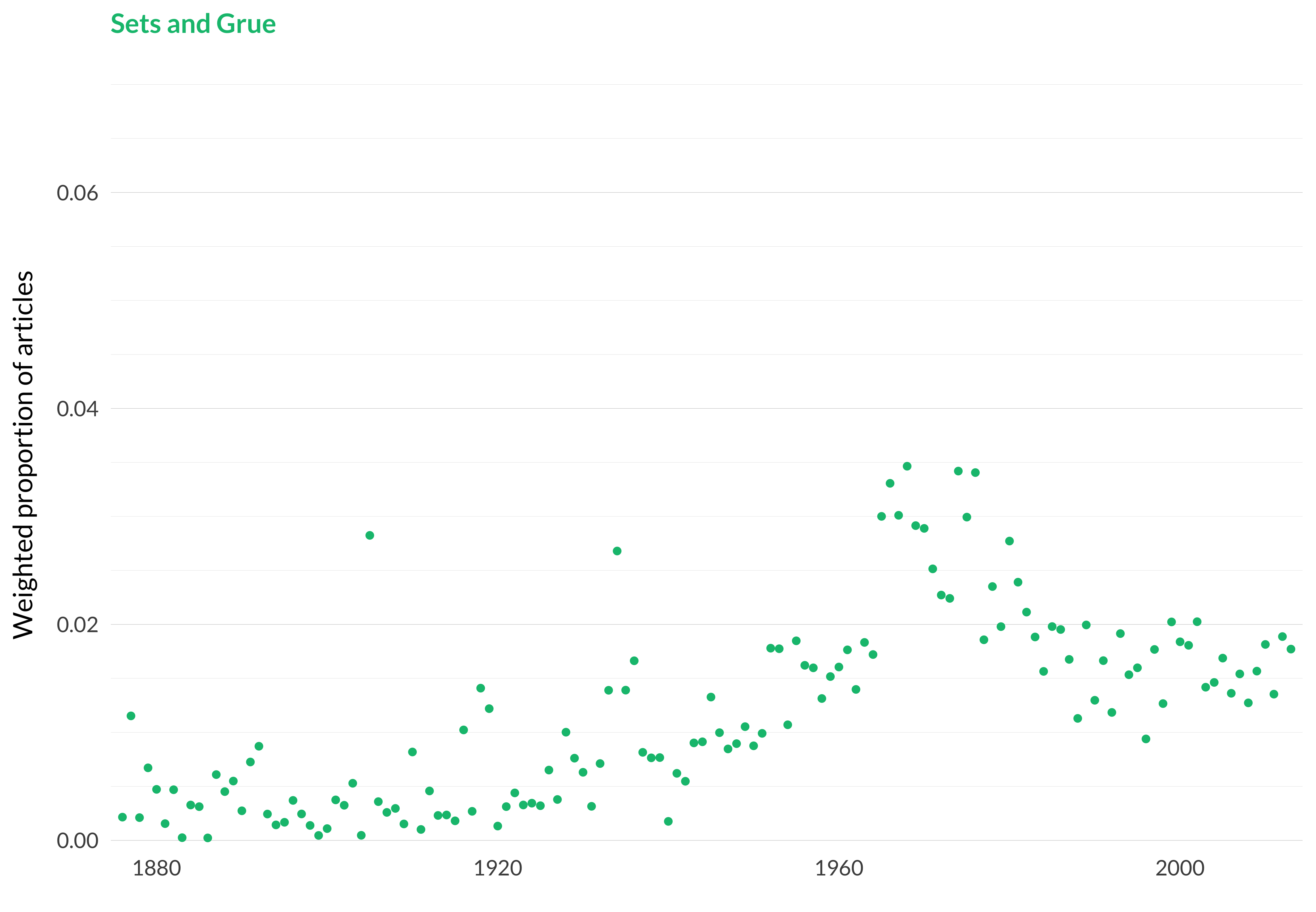
Figure 2.90: Sets and grue.
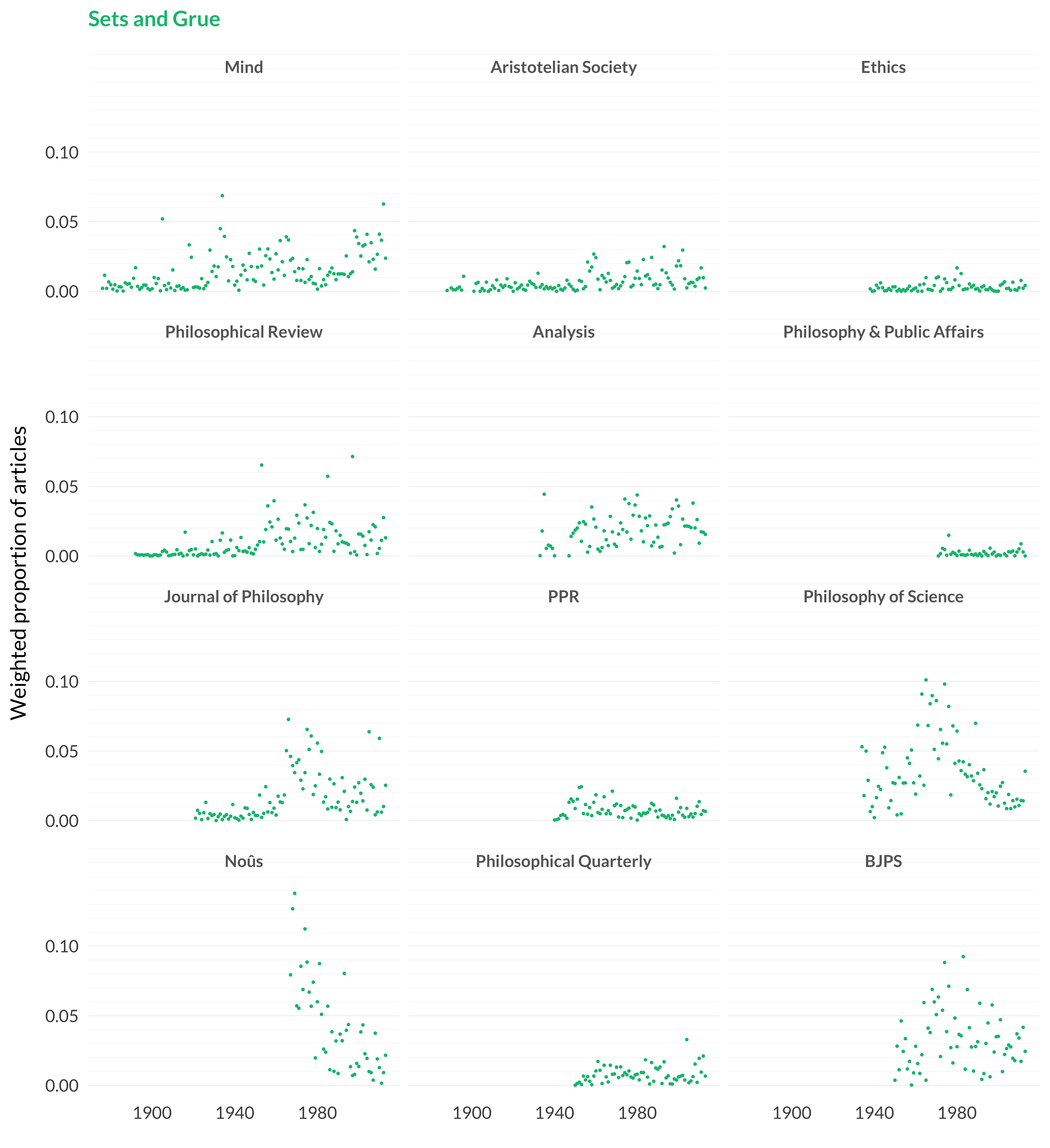
Figure 2.91: Sets and grue articles in each journal.
Comments
This is just about the paradigm example of the model finding a disjunctive topic. It knew that it wanted to put the articles on set theory in one place. And it knew that it wanted to put the articles on the grue paradox in one place. And it didn’t have enough places to put them all, so it put both of them here.
The two topics aren’t wholly unconnected; they are both problems for the kind of philosophical world view that Nelson Goodman wanted to endorse. And, of course, Goodman himself had important views on how to solve each of them. But we shouldn’t go overboard trying to figure out why the model put them in one place. Most model runs had these topics separated.
As can be seen from the highly cited articles list the model also put some articles on puzzles about verisimilitude in here. That makes more sense. Like the grue paradox, that’s a puzzle about how to manage ampliative reasoning using just the tools of formal logic.
Because the topic is so disjunctive, it lends itself reasonably well to a binary sort. So I took the 555 articles the model found, and generated a two-topic LDA from just those articles.
Here are the top fifty articles in what it called topic 1.
It’s very confident about its binary sort, as is clear from the probabilities. (I’ve normally been doing these to four significant figures, but I needed six here just to get any distinctions.) But some of these are articles that it was not confident were in the category in the first place. Let’s instead sort articles by the product of their probability of being in topic 37 (i.e., sets and grue) and their probability of being in subtopic 1 (which is starting to look like grue).
The first page here leads to things downstream of the grue paradox that I wasn’t particularly familiar with: work on the proper formalisation of scientific theories, and on the foundations of learning algorithms. Click onto page 2 and there are more articles by Ullian and by Zabludowski, so we’re in the mainstream of grue articles. Let’s do the same thing for articles in subtopic 2.
These aren’t a million miles from set theory, but in some cases they are a little bit distinct. Let’s have a look at what happens when crossing the probability of being in sub-topic 2 with the probability of being in topic 37.
And here we are looking at something very much like set theory.
The point of all this was to demonstrate something of the power of this method of analysis. Even when the model does something that seems wrong—like smushing together two topics that don’t really belong—we can use the very same tools to undo the mistake. Now that the topics are separated their frequency over time can be seen.
This is a graph of the distribution of those 555 articles into the two buckets (grue and sets) over time.
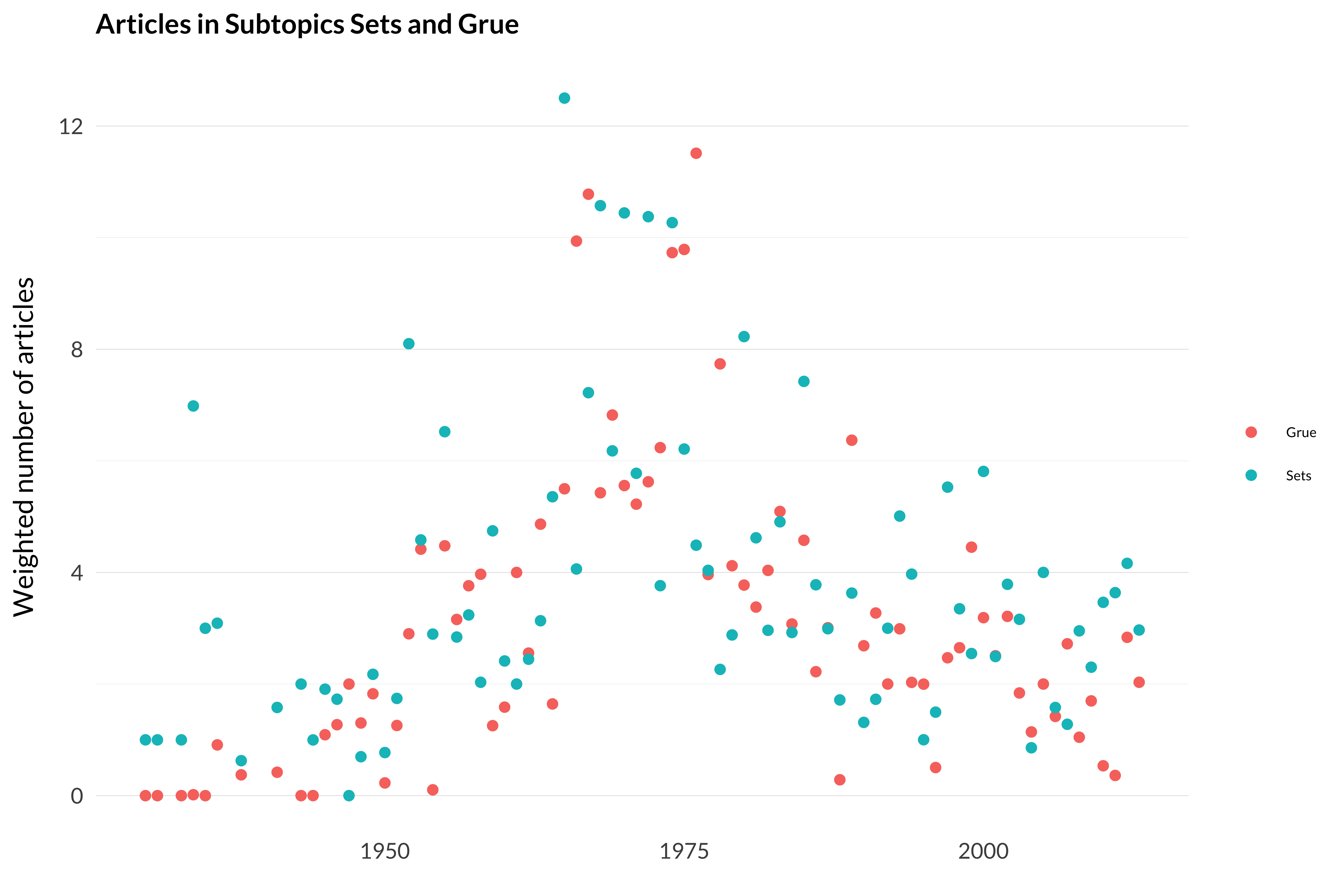
Figure 2.92: Articles on sets and articles on grue.
One can see that both of the topics peak in the late 1960s and early 1970s. And set theory doesn’t fall away quite as quickly as grue. But I had expected the difference between the two topics to get rather dramatic after 2000, and it doesn’t really. The model, somewhat sensibly, puts other work on formal learning in with grue, and this means the topic doesn’t crash away.