2.20 Classical Space and Time
Category: Metaphysics
Keywords: straight, dimensions, spaces, geometrical, dimensional, distance, spatial, figures, plane, euclidean, dimension, geometry, space, magnitude, regions
Number of Articles: 205
Percentage of Total: 0.6%
Rank: 72nd
Weighted Number of Articles: 288.9
Percentage of Total: 0.9%
Rank: 52nd
Mean Publication Year: 1960.2
Weighted Mean Publication Year: 1962.1
Median Publication Year: 1967
Modal Publication Year: 1922
Topic with Most Overlap: Ordinary Language (0.0427)
Topic this Overlaps Most With: Temporal Paradoxes (0.0469)
Topic with Least Overlap: Population Ethics (0.00017)
Topic this Overlaps Least With: Crime and Punishment (0.00036)
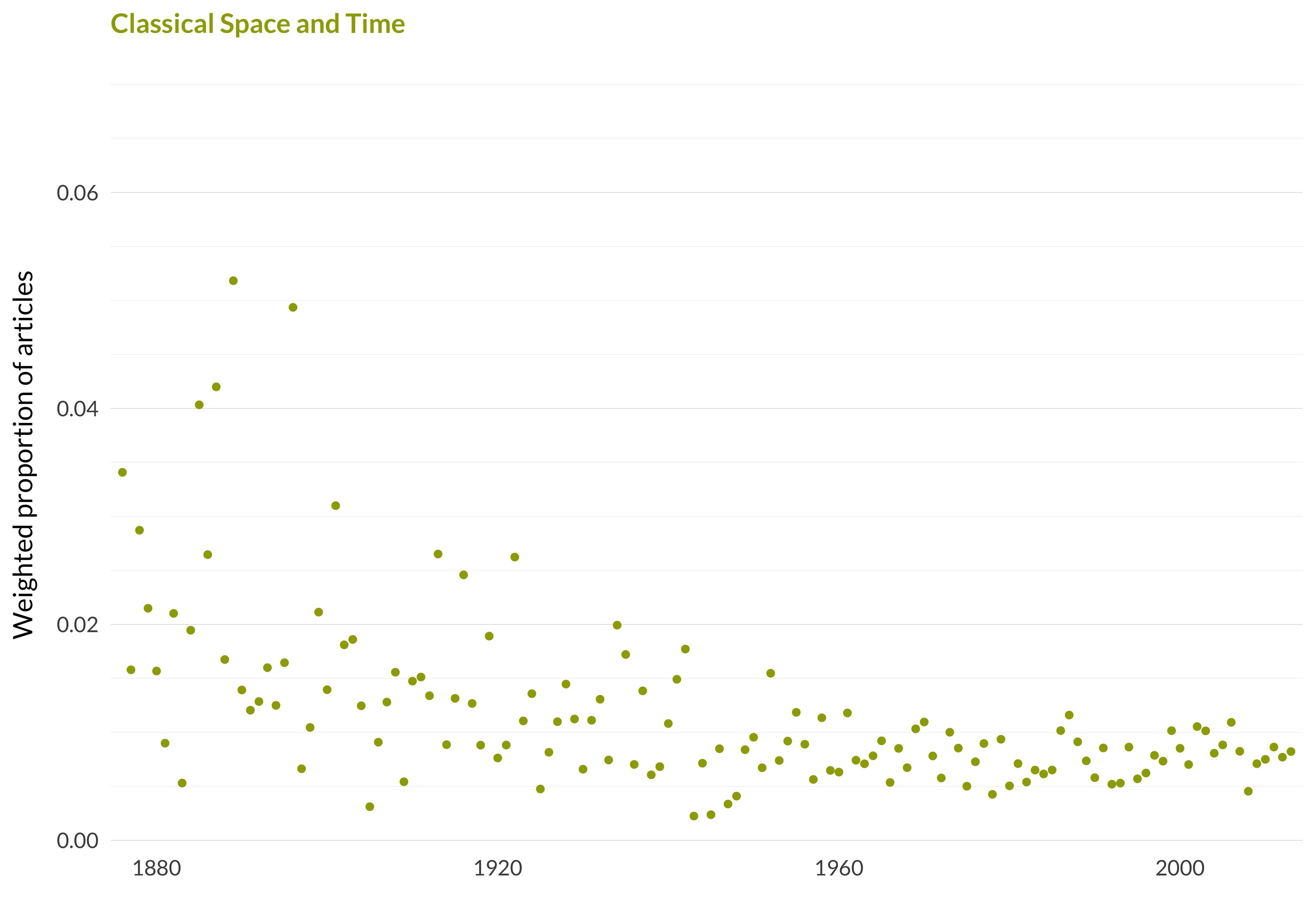
Figure 2.52: Classical space and time.

Figure 2.53: Classical space and time articles in each journal.
Comments
This topic contains a bunch of stuff on space and time in classical (i.e., prerelativistic) physics, some stuff on philosophical issues arising in geometry, and some historical work connected to those two things. It has a lot of overlap with space and time. The big differences are that this topic is more classical, and space and time is more relativistic. And space and time is considerably more technical and mathematical. I’ve used the first difference to name the topics, but the second difference is what made this go in metaphysics, while space and time goes in philosophy of science.
What I’ve called the characteristic articles for this topic turn out not to be particularly characteristic. They are the ones with the highest probability of being in the topic. But they don’t look much like the typical paper in the topic. The bulk of the articles in the topic are simply about space and time. But those articles are the ones that the model was most hesitant about clearly putting in this topic rather than space and time, and so they don’t have the highest probability of being in the topic. The articles about geometry, and about Reid, didn’t confuse the model as much, so they get listed here.
Other model runs didn’t distinguish classical from relativistic work on space time. A more standard model run ended up distinguishing work on quantum mechanics from classical and relativistic mechanics, while grouping together classical and relativistic mechanics. And with the extra topic the model had to work with, it would instead include a topic centered on the philosophy of geometry and measurement. That’s still a small topic but quite a lively one. Brent Mundy (1986, 1987) did a lot of important work in this field, which has been getting a bit of attention in recent years. I regret that this model didn’t highlight work along these lines as much as some other models did.