 My research focuses mostly on those aspects of solid mechanics
pertaining to the contact of deformable bodies and particularly
to situations in which non-uniform temperatures result from
frictional heat generation at the interface or from heat flow
across it. In such cases, thermoelastic deformation of the
contacting bodies modifies the contact pressure distribution
and can lead to a rich variety of phenomena including
localization and dynamic instabilities. These effects are
of considerable technological importance, including, for example,
non-uniform contact pressure, high local temperatures
and vibrations in clutches and braking systems: a phenomenon
known as Frictionally-excited
Thermoelastic Instability
(TEI). The figure on the left shows a transmission clutch plate after
a single engagement. The dark areas correspond to regions in which
high local temperatures have been experienced. The complete
disk in this case exhibits 12 equally spaced hot spots on
each side and they are arranged antisymmetrically. In other words,
the hot spots on the opposite side of the disk are located
in the gaps between those shown in the figure.
My research students and I
have recently developed a finite element description of
the TEI stability problem that predicts the sliding speed at
the onset of instability and the corresponding eigenmode
for practical brake or clutch designs (i.e. the number
and location of hot spots). A
windows-based software package
for estimating the susceptibility of
brake and clutch systems to TEI is available for
purchase from the University of Michigan. For more
information, including sample input and output and
a demonstration that can be downloaded,
click here.
My research focuses mostly on those aspects of solid mechanics
pertaining to the contact of deformable bodies and particularly
to situations in which non-uniform temperatures result from
frictional heat generation at the interface or from heat flow
across it. In such cases, thermoelastic deformation of the
contacting bodies modifies the contact pressure distribution
and can lead to a rich variety of phenomena including
localization and dynamic instabilities. These effects are
of considerable technological importance, including, for example,
non-uniform contact pressure, high local temperatures
and vibrations in clutches and braking systems: a phenomenon
known as Frictionally-excited
Thermoelastic Instability
(TEI). The figure on the left shows a transmission clutch plate after
a single engagement. The dark areas correspond to regions in which
high local temperatures have been experienced. The complete
disk in this case exhibits 12 equally spaced hot spots on
each side and they are arranged antisymmetrically. In other words,
the hot spots on the opposite side of the disk are located
in the gaps between those shown in the figure.
My research students and I
have recently developed a finite element description of
the TEI stability problem that predicts the sliding speed at
the onset of instability and the corresponding eigenmode
for practical brake or clutch designs (i.e. the number
and location of hot spots). A
windows-based software package
for estimating the susceptibility of
brake and clutch systems to TEI is available for
purchase from the University of Michigan. For more
information, including sample input and output and
a demonstration that can be downloaded,
click here.
 The mathematical aspects of thermoelastic contact problems are of considerable
interest and challenge. Contact mechanics is conventionally
defined by the Signorini inequalities precluding tensile
contact tractions and interpenetration of material, but
combination of these boundary conditions with simple
thermal conditions leads to an ill-posed, coupled thermoelastic
problem which exhibits counter examples to both existence and uniqueness
of the steady state. Existence problems can be resolved by
using more sophisticated boundary conditions - for example,
recognizing that the inevitable roughness of the surfaces
will impose a thermal contact resistance that depends upon
contact pressure. The quasi-fractal properties of typical
rough surfaces contributes additional interest to such formulations
and there remain many important unanswered questions about
the effect of fine scale surface statistics on thermal, mechanical and electrical contact. Interaction between thermoelastic
deformation and a pressure dependent thermal contact resistance
can be unstable, leading to non-uniform contact pressure.
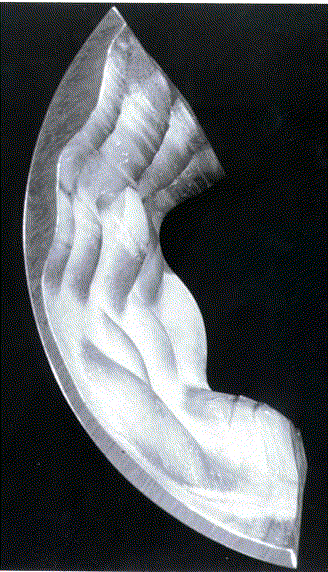
The figure on the right shows a section cut from an interrupted
continuous casting process. The sinusoidal perturbation in
the solidification boundary was caused by thermoelastic
instability associated with the mould/casting contact interface.
The mathematical aspects of thermoelastic contact problems are of considerable
interest and challenge. Contact mechanics is conventionally
defined by the Signorini inequalities precluding tensile
contact tractions and interpenetration of material, but
combination of these boundary conditions with simple
thermal conditions leads to an ill-posed, coupled thermoelastic
problem which exhibits counter examples to both existence and uniqueness
of the steady state. Existence problems can be resolved by
using more sophisticated boundary conditions - for example,
recognizing that the inevitable roughness of the surfaces
will impose a thermal contact resistance that depends upon
contact pressure. The quasi-fractal properties of typical
rough surfaces contributes additional interest to such formulations
and there remain many important unanswered questions about
the effect of fine scale surface statistics on thermal, mechanical and electrical contact. Interaction between thermoelastic
deformation and a pressure dependent thermal contact resistance
can be unstable, leading to non-uniform contact pressure.
The figure on the right shows a section cut from an interrupted
continuous casting process. The sinusoidal perturbation in
the solidification boundary was caused by thermoelastic
instability associated with the mould/casting contact interface.
The classical Coulomb friction law (also governed by instabilities)
introduces additional existence, uniqueness and stability problems.
Frictional vibrations have long been known to occur in many physical
systems, but traditional explanations have depended on the friction
coefficient being a function of sliding speed. Recent work shows
that instabilities (including `stick-slip' vibrations)
can arise with a constant coefficient of friction.
Solution of Elasticity Problems
I have developed Maple and Mathematica files for the solution of boundary-value problems in Elasticity in conjunction with my book `Elasticity'. To explore this resource, start by
clicking on either Programming in Maple or Programming in
Mathematica and then on to `Catalogue of Maple
files' or `Catalogue of Mathematica files'. If you have never used these methods to solve problems,
you will surprised how effective they are. You will however need
to have Mathematica or Maple installed on your computer system.
Software for determining the elastic fields at singular points
An analytical tool has been developed for determining the nature of the stress and displacement fields near a fairly general singular point in linear elasticity. For more information, click here.
Selected Publications
Click here for a full list of publications.
![[Portrait]](jbarber6.jpg)
 My research focuses mostly on those aspects of solid mechanics
pertaining to the contact of deformable bodies and particularly
to situations in which non-uniform temperatures result from
frictional heat generation at the interface or from heat flow
across it. In such cases, thermoelastic deformation of the
contacting bodies modifies the contact pressure distribution
and can lead to a rich variety of phenomena including
localization and dynamic instabilities. These effects are
of considerable technological importance, including, for example,
non-uniform contact pressure, high local temperatures
and vibrations in clutches and braking systems: a phenomenon
known as Frictionally-excited
Thermoelastic Instability
(TEI). The figure on the left shows a transmission clutch plate after
a single engagement. The dark areas correspond to regions in which
high local temperatures have been experienced. The complete
disk in this case exhibits 12 equally spaced hot spots on
each side and they are arranged antisymmetrically. In other words,
the hot spots on the opposite side of the disk are located
in the gaps between those shown in the figure.
My research students and I
have recently developed a finite element description of
the TEI stability problem that predicts the sliding speed at
the onset of instability and the corresponding eigenmode
for practical brake or clutch designs (i.e. the number
and location of hot spots). A
windows-based software package
for estimating the susceptibility of
brake and clutch systems to TEI is available for
purchase from the University of Michigan. For more
information, including sample input and output and
a demonstration that can be downloaded,
click here.
My research focuses mostly on those aspects of solid mechanics
pertaining to the contact of deformable bodies and particularly
to situations in which non-uniform temperatures result from
frictional heat generation at the interface or from heat flow
across it. In such cases, thermoelastic deformation of the
contacting bodies modifies the contact pressure distribution
and can lead to a rich variety of phenomena including
localization and dynamic instabilities. These effects are
of considerable technological importance, including, for example,
non-uniform contact pressure, high local temperatures
and vibrations in clutches and braking systems: a phenomenon
known as Frictionally-excited
Thermoelastic Instability
(TEI). The figure on the left shows a transmission clutch plate after
a single engagement. The dark areas correspond to regions in which
high local temperatures have been experienced. The complete
disk in this case exhibits 12 equally spaced hot spots on
each side and they are arranged antisymmetrically. In other words,
the hot spots on the opposite side of the disk are located
in the gaps between those shown in the figure.
My research students and I
have recently developed a finite element description of
the TEI stability problem that predicts the sliding speed at
the onset of instability and the corresponding eigenmode
for practical brake or clutch designs (i.e. the number
and location of hot spots). A
windows-based software package
for estimating the susceptibility of
brake and clutch systems to TEI is available for
purchase from the University of Michigan. For more
information, including sample input and output and
a demonstration that can be downloaded,
click here.  The mathematical aspects of thermoelastic contact problems are of considerable
interest and challenge. Contact mechanics is conventionally
defined by the Signorini inequalities precluding tensile
contact tractions and interpenetration of material, but
combination of these boundary conditions with simple
thermal conditions leads to an ill-posed, coupled thermoelastic
problem which exhibits counter examples to both existence and uniqueness
of the steady state. Existence problems can be resolved by
using more sophisticated boundary conditions - for example,
recognizing that the inevitable roughness of the surfaces
will impose a thermal contact resistance that depends upon
contact pressure. The quasi-fractal properties of typical
rough surfaces contributes additional interest to such formulations
and there remain many important unanswered questions about
The mathematical aspects of thermoelastic contact problems are of considerable
interest and challenge. Contact mechanics is conventionally
defined by the Signorini inequalities precluding tensile
contact tractions and interpenetration of material, but
combination of these boundary conditions with simple
thermal conditions leads to an ill-posed, coupled thermoelastic
problem which exhibits counter examples to both existence and uniqueness
of the steady state. Existence problems can be resolved by
using more sophisticated boundary conditions - for example,
recognizing that the inevitable roughness of the surfaces
will impose a thermal contact resistance that depends upon
contact pressure. The quasi-fractal properties of typical
rough surfaces contributes additional interest to such formulations
and there remain many important unanswered questions about