

Figure 1 shows one of the plates of a typical multidisk wet clutch
after a period of normal service.
The dark areas correspond to regions in which high local temperatures
have been experienced. Evidence of surface melting
can be found in extreme cases. In addition, transfer of
friction material components and the products of overheated
transmission fluid may be involved. The pattern seen in
Figure 1 represents the effect of multiple engagements
of the clutch and shows several series of hot spots
at different locations overlayed on each other.
 A better
picture of the phenomenon is obtained if the clutch is
examined after a single engagement, in which case the
regular pattern shown in Figure 2 is obtained. The complete
disk in this particular case exhibits 12 equally spaced hot spots
on each side and they are arranged antisymmetrically.
In other words, the hot spots on the opposite side of the
disk are located in the gaps between those shown in the
figure.
A better
picture of the phenomenon is obtained if the clutch is
examined after a single engagement, in which case the
regular pattern shown in Figure 2 is obtained. The complete
disk in this particular case exhibits 12 equally spaced hot spots
on each side and they are arranged antisymmetrically.
In other words, the hot spots on the opposite side of the
disk are located in the gaps between those shown in the
figure.
Despite the considerable idealizations involved in Lee's theory, it provides plausible predictions for the critical speed and the mode shape in typical brake assemblies and is therefore quite widely used in the brake and clutch industry for TEI analysis. However, there is a clear need for a method that will account for other features of the system geometry, such as the finite width of the sliding surface, the axisymmetric geometry of the disk and the `hat' section used to attach the disk to its support. One approach is to use the finite element method to solve the coupled transient thermoelastic contact problem in time (Zagrodzki 1990, Johannson 1993, Zagrodzki et al. 1999). This method is extremely flexible, in that it can accommodate non-linear or temperature-dependent constitutive behaviour, more realistic friction laws and practical loading cycles. However, it is also extremely computer-intensive and appears unlikely to be a practical design tool for three-dimensional problems in the foreseeable future.
Du's method rests on the assumption that the dominant perturbation has a real growth rate. The limited range of problems that have been solved analytically suggest that this assumption is justified if one of the two sliding bodies is a thermal insulator, or if the dominant perturbation is independent of the coordinate in the sliding direction, as in `banding' instabilities in axisymmetric systems, where the frictional heating is concentrated in an axisymmetric annular band within the contact area. However, a rigorous proof of this result has never been advanced. When both materials are thermally conducting, the stability boundary is generally determined by a disturbance that migrates with respect to both bodies in or opposed to the direction of sliding (Burton et al. 1973). In a stationary frame of reference, the perturbation will then appear to oscillate in time, corresponding to a complex exponential growth rate. The migration speed is smaller relative to the better thermal conductor and this relative motion approaches zero when the other body tends to the limit of thermal insulation. Practical systems such as brakes and clutches usually involve a steel or cast iron disk sliding against a composite friction material of significantly lower conductivity (typically two orders of magnitude lower than that of steel). As a result, the dominant perturbation migrates only very slowly relative to the metal disk. However, this migration plays an important part in the process, because it reduces the thermal expansion due to a given perturbation in heat input and hence increases the critical speed.
We first assume that the temperature, stress and displacement fields can be written as the product of a function of the spatial coordinates and an exponential function of time When these expressions are substituted into the governing equations and boundary conditions of the problem, the exponential factor cancels and we are left with a modified system of equations in which the growth rate appears as a linear parameter. A finite element discretization of this modified problem then yields a linear eigenvalue problem for the growth rate.
In order to adapt this method to the sliding contact problem, we need to choose a suitable frame of reference, relative to which at least one of the bodies will necessarily be moving. This introduces convective terms into the heat conduction equation and can present numerical problems when the convective term is large (Christie et al. 1976). The relative magnitude of convective and diffusive terms can be assessed by calculating the Peclet number Pe = Va/k, where V is the convective velocity, k is the thermal diffusivity and a is a representative length scale. Peclet numbers in tribological applications are typically very large. For example, a steel clutch disk of mean diameter 0.2 m rotating at 2000 rpm corresponds to a Peclet number of about 35,000 using the mean diameter for a and even the element Peclet number will be large compared with unity for a realistic discretization. Thus, the convective terms will tend to dominate the finite element solution.
Fortunately, difficulties with convective terms can be avoided by using Fourier reduction in the sliding direction as long as (i) no material points on either sliding body experience intermittent contact and (ii) periodic boundary conditions apply in the sliding direction. These conditions are satisfied for multidisk brakes and clutches, which have an axisymmetric geometry, but which often exhibit signs of damage attributable to TEI with a non-axisymmetric eigenmode, as shown in the figures above. In this case, orthogonality arguments show that all the eigenmodes must have Fourier form in the circumferential direction and the sinusoidal function can be factored out of the equations, leading to an eigenvalue problem in radial and axial coordinates only, for given values of wavenumber and rotational speed. A finite element description of this problem leads to a linear eigenvalue problem for the growth rate.
 This method has been implemented in a
windows-based software package
that is available for purchase from the University of Michigan.
Here we apply the method to the practical
clutch design shown in Figure 3. The design
parameters and material properties were chosen to be consistent
with the clutch whose
experimentally damaged disks were shown above.
The clutch has three steel stators and two composite rotors.
The rotors each have a steel core and a friction material layer
bonded onto each side. During operation, sliding occurs between the
friction material layers and the adjacent stators. A hydraulic
pressure, P is applied to the upper piston, causing the
stack of disks to be compressed against the lower reaction
plate. The corresponding boundary conditions on the
(homogeneous) perturbation problem are therefore that
the upper surface of the piston be traction-free
and the lower surface of the end plate be restrained from axial motion.
All exposed surfaces were assumed to be thermally
insulated, since practical heat transfer coefficients are so
small that they hardly affect thermoelastic instability.
This method has been implemented in a
windows-based software package
that is available for purchase from the University of Michigan.
Here we apply the method to the practical
clutch design shown in Figure 3. The design
parameters and material properties were chosen to be consistent
with the clutch whose
experimentally damaged disks were shown above.
The clutch has three steel stators and two composite rotors.
The rotors each have a steel core and a friction material layer
bonded onto each side. During operation, sliding occurs between the
friction material layers and the adjacent stators. A hydraulic
pressure, P is applied to the upper piston, causing the
stack of disks to be compressed against the lower reaction
plate. The corresponding boundary conditions on the
(homogeneous) perturbation problem are therefore that
the upper surface of the piston be traction-free
and the lower surface of the end plate be restrained from axial motion.
All exposed surfaces were assumed to be thermally
insulated, since practical heat transfer coefficients are so
small that they hardly affect thermoelastic instability.
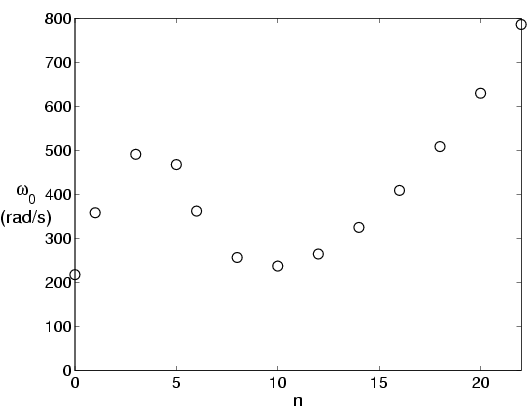 The critical speed for the five disk clutch system is
shown in Figure 4 as a function of wavenumber n.
Instability first occurs in the banding mode (n=0) at a
rotational speed of 218 rad/s, but there is also a local
minimum of 237 rad/s at n=10. This clutch is designed
for initial engagement speeds of 628 rad/s,
so we also calculated the exponential growth rate
at this speed. The maximum value of b=39.6 (1/s)
corresponds to the Fourier mode with 10 hot spots
per revolution, whilst the banding mode grows only at
a rate of 12.2 (1/s). Thus, the non-axisymmetric
mode would be expected to be dominant in this application.
The critical speed for the five disk clutch system is
shown in Figure 4 as a function of wavenumber n.
Instability first occurs in the banding mode (n=0) at a
rotational speed of 218 rad/s, but there is also a local
minimum of 237 rad/s at n=10. This clutch is designed
for initial engagement speeds of 628 rad/s,
so we also calculated the exponential growth rate
at this speed. The maximum value of b=39.6 (1/s)
corresponds to the Fourier mode with 10 hot spots
per revolution, whilst the banding mode grows only at
a rate of 12.2 (1/s). Thus, the non-axisymmetric
mode would be expected to be dominant in this application.
 The eigenfunction for temperature in the stator surface is
shown on the left for the n=10 mode.
Comparison of this figure with the experimental observations
of Figure 2 above shows that the perturbation analysis
correctly predicts an antisymmetric mode with focal hot
spots, but the dominant wavenumber is predicted to be 10
in contrast to the 12 hot spots observed experimentally.
Various explanations might be advanced for this relatively small
discrepancy. The initial speed for clutch engagement is well above
the predicted critical value and all wavenumbers between
4 and 14 are unstable at the beginning of the engagement.
However, the mode with wavenumber 10 has the highest
growth rate and would be expected to dominate the transient
process. A more plausible explanation is that clutch friction
materials exhibit quite complex constitutive behaviour and
it is difficult to select an appropriate incremental
elastic modulus for the analysis. The modulus used in the
finite element analysis was the incremental modulus obtained in compression
tests at the mean engagement pressure, but significant
stiffening may occur under service conditions. The critical
speed and the dominant eigenmode are both quite sensitive
to the modulus of the friction material and plausible values
could have been chosen to `fit' the theoretical predictions
to a wavenumber of 12. This highlights the fact that the
principal difficulty remaining in obtaining reliable theoretical
predictions for TEI performance lies in the accurate
characterization of the properties of the complex friction
materials used.
The eigenfunction for temperature in the stator surface is
shown on the left for the n=10 mode.
Comparison of this figure with the experimental observations
of Figure 2 above shows that the perturbation analysis
correctly predicts an antisymmetric mode with focal hot
spots, but the dominant wavenumber is predicted to be 10
in contrast to the 12 hot spots observed experimentally.
Various explanations might be advanced for this relatively small
discrepancy. The initial speed for clutch engagement is well above
the predicted critical value and all wavenumbers between
4 and 14 are unstable at the beginning of the engagement.
However, the mode with wavenumber 10 has the highest
growth rate and would be expected to dominate the transient
process. A more plausible explanation is that clutch friction
materials exhibit quite complex constitutive behaviour and
it is difficult to select an appropriate incremental
elastic modulus for the analysis. The modulus used in the
finite element analysis was the incremental modulus obtained in compression
tests at the mean engagement pressure, but significant
stiffening may occur under service conditions. The critical
speed and the dominant eigenmode are both quite sensitive
to the modulus of the friction material and plausible values
could have been chosen to `fit' the theoretical predictions
to a wavenumber of 12. This highlights the fact that the
principal difficulty remaining in obtaining reliable theoretical
predictions for TEI performance lies in the accurate
characterization of the properties of the complex friction
materials used.
Notice that the axisymmetric mode in this example has the lowest critical speed but that a non-axisymmetric mode becomes dominant at larger speeds. The general solution of the transient thermoelastic contact problem at constant sliding speed can be written down as an eigenfunction expansion. Furthermore, the fact that some of these terms grow exponentially but that most decay suggests that a severely truncated series (a reduced order model) might give a highly efficient numerical approximation to the transient behaviour, whilst retaining adequate accuracy. This is the subject of an ongoing investigation.
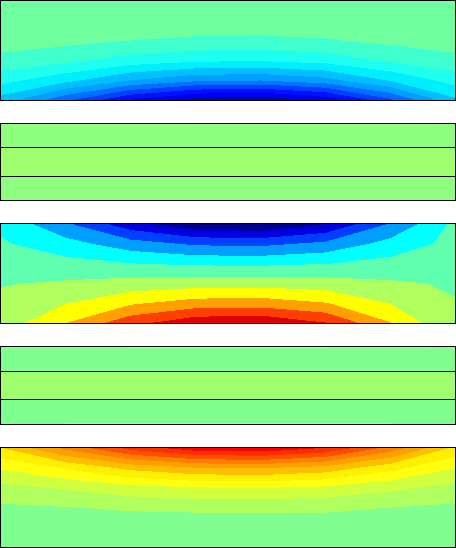 The corresponding
temperature contours in the (r,z) plane predicted for the
dominant eigenmode are shown on the right.
Notice that the eigenmode is antisymmetric with
respect to the central stator, in which the greatest
temperature perturbations are recorded. The temperatures in
the rotors are close to zero except in a thermal boundary
layer that is too thin to be visible in the figure.
The two rotors exhibit a `qualitative'
symmetry in the sense that hot regions occur at the same
locations on the two sides, but the maximum temperatures
are lower on those surfaces nearest to the piston and the
end plate. Both these predictions were confirmed by
the experimental observations. The most severe damage was
observed on the central steel disk and the location of
hot spots on the other two stators indicated a mode symmetric
with respect to the rotors. The attenuation of the
disturbance near the ends of the disk stack is probably
attributable to the extra rigidity provided to the terminal
stators by the piston and end plate. In fact, a simpler model in
which the piston and end plate were replaced by rigid
non-conducting surfaces predicted a critical speed within 1% of
the more exact value.
The corresponding
temperature contours in the (r,z) plane predicted for the
dominant eigenmode are shown on the right.
Notice that the eigenmode is antisymmetric with
respect to the central stator, in which the greatest
temperature perturbations are recorded. The temperatures in
the rotors are close to zero except in a thermal boundary
layer that is too thin to be visible in the figure.
The two rotors exhibit a `qualitative'
symmetry in the sense that hot regions occur at the same
locations on the two sides, but the maximum temperatures
are lower on those surfaces nearest to the piston and the
end plate. Both these predictions were confirmed by
the experimental observations. The most severe damage was
observed on the central steel disk and the location of
hot spots on the other two stators indicated a mode symmetric
with respect to the rotors. The attenuation of the
disturbance near the ends of the disk stack is probably
attributable to the extra rigidity provided to the terminal
stators by the piston and end plate. In fact, a simpler model in
which the piston and end plate were replaced by rigid
non-conducting surfaces predicted a critical speed within 1% of
the more exact value.
This explanation also suggests that a more exact sequence of antisymmetric and symmetric perturbations in the stators and rotors respectively would be observed in a clutch with a larger number of disks. This was confirmed by additional finite element calculations for clutches of the same form, but with odd numbers of disks between 3 and 13. The critical speed decreases towards a limit as the number of disks increases and the dominant mode approaches a state in which the perturbation is strictly antisymmetric in the steel disks and symmetric in the composite disks, except for those near to the ends of the stack. This limiting condition was also obtained independently by modelling half of one rotor and one stator, using symmetric/antisymmetric boundary conditions at the respective mid-planes. The number of hot spots in the dominant eigenmode increases slightly with the number of disks, but the solution has essentially converged on the limit for clutches with 11 disks or more.
In conventional clutch systems with alternating steel and composite disks, the dominant unstable mode is usually antisymmetric with respect to the steel disks, symmetric with respect to the composite disks and involves an integer number of focal hot spots around the circumference. This prediction is confirmed by experimental observations of thermal damage in a 5 disk clutch.
The method is easily applied to other examples and can therefore be used to assess the effect of design modifications such as changes in geometry and material properties on the thermoelastic stability of multidisk brakes and clutches.