|
Vertically, the middle of the graph is level 0. The level of -1 (100% of a comma flat: Dbb over to Ab) is to the bottom/left, and +1 (100% of a comma sharp: D# over to Gx) to the top/right.
The horizontal lines show the broken layout that occurs if a keyboard is set up in the normal 18th century orchestral standard, "1/6 comma" tuning. The notes in the middle section are all in tune with one another, level on the same layer, emphasizing harmony. The notes to the left of E-flat are all one comma too flat, and the notes to the right of G-sharp are all one comma too sharp. That is, each time we travel twelve notes in either direction for an enharmonic note-name, we must add one comma to get to the next layer. (Notes such as Eb and D# really are different from one another. 18th century musicians were trained to sing and play them with an understanding of that difference, inflecting chromatic semitones smaller melodically than diatonic semitones.) Intervals that include notes across the gaps have a "wolf" quality to them, due to the misspelling of the intonation. There are eleven similar fifths and one wolf diminished sixth; eight similar major thirds and four wolf diminished fourths.
The diagonal on this chart shows equal temperament: all its notes are exactly the same distance apart, geometrically. Therefore, all the major or minor scales in equal temperament have the same "shape" or character as one another, a steady slope. Modulation does not accomplish very much, because each new scale we go to sounds the same. Equal temperament emphasizes melodic smoothness, with a bland equality of chromatic and diatonic semitones: it becomes hardly relevant to spell the note names correctly.
Bach's temperament, the plotted zigzag here, bridges those rough gaps by making the notes gradually blended from one layer to the next.
The numerals below each column here indicate the percentage of the Pythagorean comma in deviation from the regularity of extended 1/6 comma temperament.
B and the sharps are at tastefully compromised positions, tuned rather high so they can serve also as flats; and each of these is differently compromised, giving each note a subtle "personality" distinct from regularity.
Every scale sounds different from every other, because each subset of seven consecutive notes has a different shape in the relationships of those notes. (Make a little template, or use your fingers, to look at only seven notes
at a time. Then move it left or right, and notice how the shape of the plotted Bach curve across
seven notes is different
for each of the twelve starting points.) C major is the most like regular "1/6 comma" tuning, with a simple and gentle sound, because six of its seven notes are in those normal horizontal positions. A-flat major (notes Db to G) is the most like equal temperament, as the slope is most similar to that diagonal. E major (A to D#) resembles the steeper slope of Pythagorean tuning.
As a reminder: the Bach layout, in terms of fifths tempered by comma fragments, is
F -1/6 C -1/6 G -1/6 D -1/6 A -1/6 E 0 B 0 F# 0 C# -1/12 G# -1/12 D# -1/12 A# (+1/12 F).
For more about this generation of diatonic scales from a series of fifths, see Easley Blackwood's book
The Structure of Recognizable Diatonic Tunings, 1985.
Sorge's analysis scheme for major thirds is explained well in several articles by Mark Lindley, and here.
Functions of accidental sharps/flats/naturals within tonal music
"Accidentals" are the intrusions of sharps, flats, or naturals into a musical passage.
By altering some of the scale steps upward or downward by a semitone, they effectively
move us into a different and neighboring diatonic scale. The accidental alerts the ear
that we are changing the scale. This is akin to hexachord mutations in older systems.
For example: if the music is going along in C major, and some occurrences of F# intrude,
we know that we have now shifted to be in G major. The F# is a member of the G major scale,
being exchanged for the F natural that we had in C major. We will probably not hear any more
occurrences of F natural for a while, until the music modulates back toward C major and cancels
the F# back to F natural.
Another example: some music is in C minor, and then at some melodic place where we might expect
an E-flat we hear an E natural instead. That E natural tells us that the music is now perhaps
approaching F minor (with its C-E-G dominant triad), or perhaps shifting from C minor directly
into the parallel C major.
It is also possible that we are headed into a modulation to E-flat major: via F minor (ii),
Bb major (V), Eb major (I) in the "circle of 5ths" with secondary dominants. The point is that the
E natural itself alerts us: we are going somewhere away from C minor.
The accidental is a surprise into the texture. It draws attention.
A raised note is typically visible in the score as an accidental sharp sign (#),
if we are in a passage that is mostly written with naturals. Or, the raising might be done with
a double-sharp sign (x) if we are already in a context of many sharps. Or, it might occur as a
natural sign within flat-key music, to cancel one of the flats (b).
Similarly, a lowered note is a flat within a passage of naturals; or a double-flat (bb) within
a passage of flats; or a natural to cancel a sharp.
Here are some of the most frequently seen/heard functions of the raised or lowered notes,
within tonal music. These are post-rationalized "rules" of behavior from studying Bach chorales, keyboard music,
ensemble music, violin/cello/flute solos, etc. with the questions: "When an accidental pops up, what is the
music doing and where is it going next? What is the altered note doing, functionally, beyond
creating a surprise within the texture?"
Raised note (sharp, double-sharp, or natural)
- generally moves us toward the dominant, in modulation direction
- major 3rd of the dominant, V...which is additionally a color change from minor to major, if we are within a minor-scale passage
- leading tones, melodically tending upward
- 2nd or 3rd degrees of the scale in secondary dominants
- sharpened root of unexpected fully-diminished 7th chords...moving toward II, V, or I
- 6th and 7th scale degrees leading upward in melodic minor
- raised 5th degree of secondary dominants, changing a tritone to a perfect 5th
Lowered note (flat, double-flat, or natural)
- generally moves us toward the subdominant, in modulation direction
- new tonic resulting from subdominant motion
- 4th degree of a major subdominant scale, IV
- the minor 7th in a major/minor dominant 7th chord...often occurring on I or i, to tonicize IV or iv
- 3rd or 6th degree of minor subdominant scale, iv
- 7th degree on top of a fully-diminished 7th chord, approaching a dominant area
- minor 9th of a dominant
- the new root and 5th degrees of a surprising shift to VI of the minor mode (such as sudden movement from C major to an A-flat major chord)
Interactions with keyboard temperament
Now, how does this bring us back to the present keyboard temperament?
Please refer again to the graph of enharmonic placements, above. In this particular temperament,
when the accidentals occur to raise or lower a note, it not only moves us toward some new key (usually),
but it also violates our expectations of intonation!
That is: the new note that comes in with a sharp/flat/natural is not only from some scale foreign to
the musical context, but it is also slightly higher or lower in pitch than it would be
in the regular/meantone systems. It creates an irritation, an irregularity,
that can help to draw the listener's attention toward whatever modulation is happening, tonally.
The patterns of tones and semitones have slightly different sizes, for all twelve of the major scales
and all twelve minor scales. This helps to alert the ear to the recognizably audible
"signatures" of each scale: different notes of different scale degrees are slightly off the expected
intonation, making every scale unique. Some scales seem "brighter" or "crisper" or "mellower" or "plainer"
than others, depending how many of these irregular sharps or flats they have in them.
For more about this, see the section "Recognizable scales through the distinct intonation of their steps"
in part 2 of "Bach's extraordinary temperament: Our Rosetta Stone".
In an example mentioned there, the two chords of C-D-F-B and Eb-F-Ab-D present different characters
(even though their spacing is similar, according to tones and semitones): the Eb and the Ab are more irregular
in their context than the C and F are in theirs. The entire chord inherits a differently crunchy quality,
whereas these two would be "the same" quality as one another in equal temperament, beyond the simple point
of being higher or lower in pitch overall.
Similarly, the example of E-F#-A-D# vs F#-G#-B-E# is given. These sharpened notes are differently irregular
in their intonation, and therefore the whole chord gives a somewhat different effect.
Why does this matter?
These observations about accidentals, and about tonal behavior, are not part of a historical argument
for the temperament. Rather, they are derived theoretical observations about what it does in practice to
aid the natural projection of tonal music.
The temperament gives listeners some audible clues
that the music being played is modulating, whenever these slightly irregularly-tuned accidentals intrude
into the progress of a tonal composition. It helps the music to seem more "alive" or organic as it
goes along, with gradual or sudden changes within the melodies and harmonies. The music inherits more
presence and immediacy than it does if played in equal temperament or the
regular/meantone temperaments: because regular temperaments do
not offer these slight surprises. The irritations of an irregular temperament help to capture and sustain
the interest of listeners.
(The word "irritations" here is not intended to suggest that the sounds are offensive, but merely
that they cross any expectations of regularity.)
Similar analytical observations of subtle intonation could be offered with respect to
other reasonably balanced "circulating" temperaments (usable in all 24 major/minor keys), such as those by Neidhardt, Sorge, or Marpurg. The melodic irregularities of
the intonation are a result of setting up some differently-sizes 5ths, 3rds, or both. These writers did
not devote space in their printed publications to analyze their temperaments down to this level of
tonal behavior. They simply provided sufficiently detailed instructions that the reader could set up
their temperaments accurately on a keyboard, and then play through music to hear the resulting nuances.
Regular unequal temperaments cannot offer
such subtle surprises, except on the occasions where enharmonically misspelled notes are being played.
For example, if a keyboard has a regular temperament including the note
Eb, any occurrences of D# in the music will sound somewhat odd because the sounding pitch is too high
to be a proper D# in context.
Conjecture
Here is a small item of conjecture, about perception of tonal music. It is offered also within
that article, "Bach's extraordinary temperament: Our Rosetta Stone".
Page 216: "I suspect that musical ears more readily tolerate notes that are slightly sharp than
notes that are noticeably flat within melodies. I cannot explain that phenomenon adequately."
And its footnote at that point: "Experts in the fields of musical perception and pedagogy will
surely have more to say here. At this point I can only report my own impression and expectations:
that instrumental melodies should sound reasonably vocal, and any unduly flat notes in leaps
(especially on organs) simply sound to me like poorly supported singing."
To this I would add a further conjectural suggestion, from analysis of this tonal business of
enharmonics and accidentals. Musical ears may more readily tolerate scale degrees "Mi", "Re",
and "La" that are noticeably too sharp, than "Ut" ("Do") or "Fa" that are too flat.
In some of the 18th century circulating temperaments, the occasions of a too-low "Ut" come up
most frequently when the bass line uses the accidental notes Ab, Db, or Eb; or when the functional
root of the harmony is suddenly dropping by a 3rd.
How fast do the flats fall off?
This practical smoothness of various temperaments may be measured by observing how quickly the
various flatted notes accumulate errors of a comma. That is, how far does any given note deviate
from regularity, making it seem "farther out of tune" than we might expect, and therefore drawing
attention to itself when played?
The goal (arguably!) is to have the notes slightly out of tune, enough that they contribute
liveliness to the texture without seeming outright "wrong" or poorly placed. The latter happens if
the note is approximately 100% of the comma, or more, off the expected point. Some listeners might
draw their line of tolerability nearer 75%; or others might hear wayward intonation more forgivingly
through 125% or more.
This field of musical perception needs more work, in such contexts of tonal
music played in various irregular keyboard temperaments. The following table is offered as a
possible impetus in that direction.
My standard measurement here is the same that I use in the rows "Error % PC" and "Enharm err % PC" of my usual
analytical layouts. As we go around the circle/spiral of 5ths flatward, how much of a Pythagorean comma
error accumulates as we approach the enharmonic respelling of the "same" note? (For example, C being respelled
as Dbb, via the sequence: C-F-Bb-Eb-Ab-Db-Gb-Cb-Fb-Bbb-Ebb-Abb-Dbb.) If we could use a keyboard with 55 notes
to the octave, akin to regular 1/6 PC temperament, we could keep all those errors to 0%, and our Dbb would be
exactly 1 Pythagorean Comma higher in pitch than C...and played with a different key lever on the keyboard.
But, if we have to restrict ourselves to only 12 notes per octave, each temperament must find a way to burn off
100% of a PC each time we do twelve flatward steps, by 5ths. "Clear as mud?"
These are all calibrated together with C=0. Everything is rounded off to the nearest integer, as a percent
of the comma. ("50" means 50%, i.e. 1/2 Pythagorean comma....)
The higher the number shown here, for the other notes, the higher the percentage that it's flat.
And the higher the number, the worse that note tends to do as a tonic for major-key music.
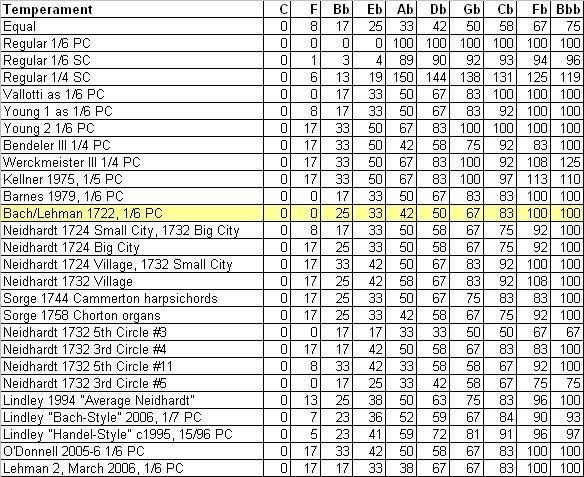
Some observations:
The main temperament discussed in this web site is shown here in yellow. It is what sounds normal to me,
both from the reasoning I have presented in the various papers here (i.e. that I believe it was Bach's own
system for at least his WTC!), and because I have spent several years playing in it on harpsichords, clavichord,
pianos, and organs.
Whenever I listen to anyone else's recordings or performances that are tuned in Kellner's
temperament, or Werckmeister III, I am bothered in both melodic and harmonic perception by the way so many of
the notes seem excessively flat to me...especially Eb, Ab, Db, and Gb. I especially notice this in music
of C minor, F minor, G minor, Eb major, and Bb major (when a chord such as Bb-D-F-Ab comes up, for example).
This is noticeable enough, at least for me, that I perceive the music as frankly ugly and misshapen,
when played in either Kellner or Werckmeister III. This might seem like a harsh judgment, but that's how I
hear it when listening closely to the music. It's as much a melodic perception as harmonic: it strikes me and
makes me as uncomfortable as out-of-tune singing does.
Equal temperament falls off smoothly and gently with these comma errors,
handling flat-key music remarkably gracefully. My main objection to it, musically, is that it's dull!
Only a few of these temperaments shown here
have the note Db placed "high enough", i.e. with a number at or below 50% flatness. Instead,
the other temperaments here favor the note C# at the expense of this Db. (For example, Kellner: the Db is 83%
flat, while the C# is correspondingly only 17% sharp; the effect within tonal contexts
is a gentle and harmonious C#, and a raucously raw Db.)
Sorge's 1758 temperament has only four notes different from Bach/Lehman 1722. Its F is 17% of a comma flatter,
Db is 8% flatter, and the Cb and Fb are each 8% sharper.
Another way of stating that comparison is: this Sorge temperament
has a "better" E# and C# at the expense of a less good F and Db;
and a "better" Cb and Fb at the expense of B and E.
The Neidhardt, Sorge, Lindley, O'Donnell, and "Lehman 2" temperaments are discussed on my pages of reaction
to the Lindley/Ortgies and O'Donnell articles.
A suggested list of Bach repertoire to test enharmonic handling is
here.
Return...

|





