LaripS.com, © Bradley Lehman, 2005-22, all rights reserved.
All musical/historical analysis here on the LaripS.com web site is the personal opinion of the author,
as a researcher of historical temperaments and a performer of Bach's music.

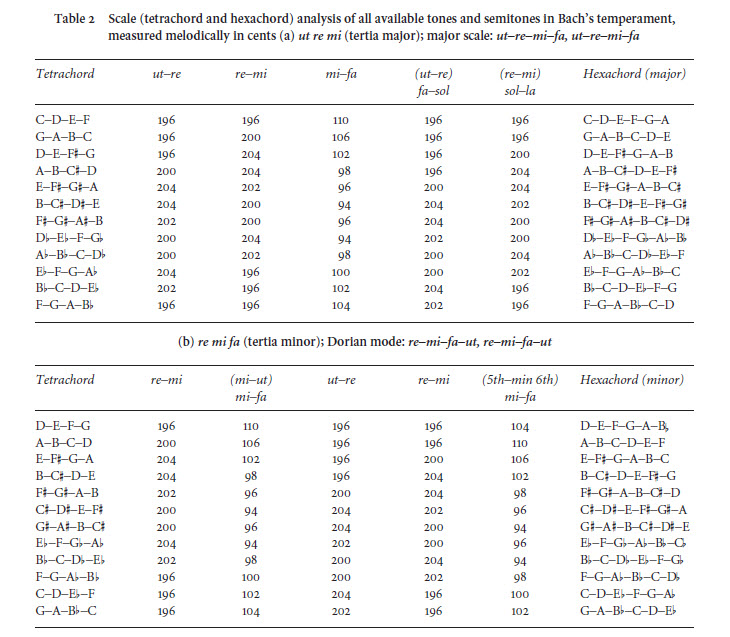
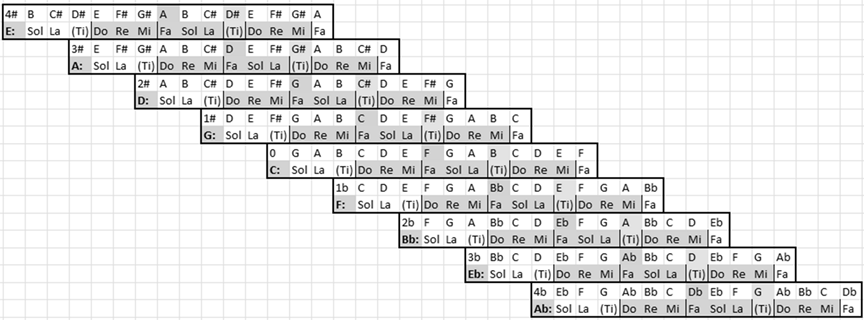
Fa, Ti, and Modulation

(Some of the illustrations....)

My 2005 article "Bach's Extraordinary Temperament: Our Rosetta Stone" looked very mathematical at some places. It gave some readers the mistaken impression that the temperament is merely a set of formulas, or that Bach's drawing was only the pretext for calculations.

Other readers missed the point that the enharmonic handling here is a vital part of the argument about matching temperaments to musical compositions. The music is itself part of the evidence, because it tells us what notes we must be able to play. A note such as C# belongs to diatonic scales such as D major, A major, E major, B minor, and others. The different note, Db, does not belong to those scales. It is a member of some other diatonic scales that do not have any C# in them. C# and Db make an enharmonic pair that never belong to the same scale, but they share one lever and one pitch on a keyboard. So, how do we tune that keyboard in a way that will let us play those notes either way, if we see that our music asks for the existence of both?

I am showing the math from 2005 again here, briefly, to say that we are moving ahead to more important music theory that is about the way the notes behave within their scales. My point with the numbers was to measure what is happening melodically and harmonically when music is played using these temperaments.

The aim was, and still is, to show how temperaments affect musical scales. The temperaments are set up by ear in a few minutes, and then we listen to them for hours or days. We don't hear numbers. We hear melodies and harmonies that either work passably, or that sound awkward (with temperaments that don't match the scale requirements of the music). Our Do-Re-Mi-Fa and our Sol-La-Ti-Do must make sense melodically...and to make that work properly, we must give plenty of attention especially to Fa, Ti, and Mi. Those are the notes that are most volatile whenever music is modulating from one scale to a different scale.

First, we need to see a bit about the comma of error (difference in pitch) between notes of an enharmonic pair, such as C# and Db. If we are expecting the C# to sound good as Ti or Mi, and the Db to sound good as Fa, we need to look at the other notes around them in those scales.

• The C# must play nicely with A, B, D, E, F#, and G#. It must also get along with G natural, which is Fa when C# is Ti.
• The Db has different neighbors. As Fa, it must get along with Ab, Bb, C, Eb, F, and G. Notice that none of these notes are related to C#'s neighbors, until we get to G. Notice also that when Db becomes Do, it is closely related to Fa at Gb. So, Gb is another important neighbor of Db.
• When Db is Fa, G is Ti. When C# is Ti, G is Fa. That's interesting. There is a diminished fifth of Ti-Fa from C# to G, and an augmented fourth of Fa-Ti from G to Db. We will return to this.
• For now, we mainly need to notice that Db is ideally a much higher pitch than C#. To make everything work with all of Db's neighbors, and with all of C#'s neighbors, and with G, we must get all of those neighboring notes to sound plausible melodically.
• If we are going to compromise the pitch of Db and C#, we must also compromise all those other neighbors somewhat, so nothing will sound far off anywhere. We must do it smoothly enough and intelligently enough so the compromises don't draw attention to themselves as "wrong notes".
• Just by talking about setting up a compromised C#/Db on a harpsichord, we are needing all of these other notes: A, Bb, B, C, (C#/Db), D, Eb, E, F, F#/Gb, G, and G#. That's 14 different notes. Those other 12 notes all "care about" the pitch we choose for our compromised C#/Db, because they must all play nicely in diatonic scales with it. Everything is intertwined and interdependent.
• Our keyboard has only 12 levers per octave. Here we are. Which other pitches need to be nudged upward or downward a little bit, so that everything still sounds like plausible A, Bb, B, C, C#, Db, D, Eb, E, F, F#, Gb, G, and G#? What do we do with musical compositions that need a different 13, 14, 15, 16, 17 notes instead of those 14 that belong near C#/Db?
• A piece like Bach's "Italian Concerto" is in the supposedly simple key of F major, but read through the entire composition to assess what it needs: Db, Ab, Eb, Bb, F, C, G, D, A, E, B, F#, C#, and G#. That's 14 different notes. The other piece in the same book, the "French Ouverture" in B minor, needs the 15 other notes of F, C, G, D, A, E, B, F#, C#, G#, D#, A#, E#, B#, and Fx. No flats.
• We can't merely glance at the key signatures like one flat or two sharps, and call it a day. To play these pieces, we must account for every note they need, and make all those scales sound plausible.

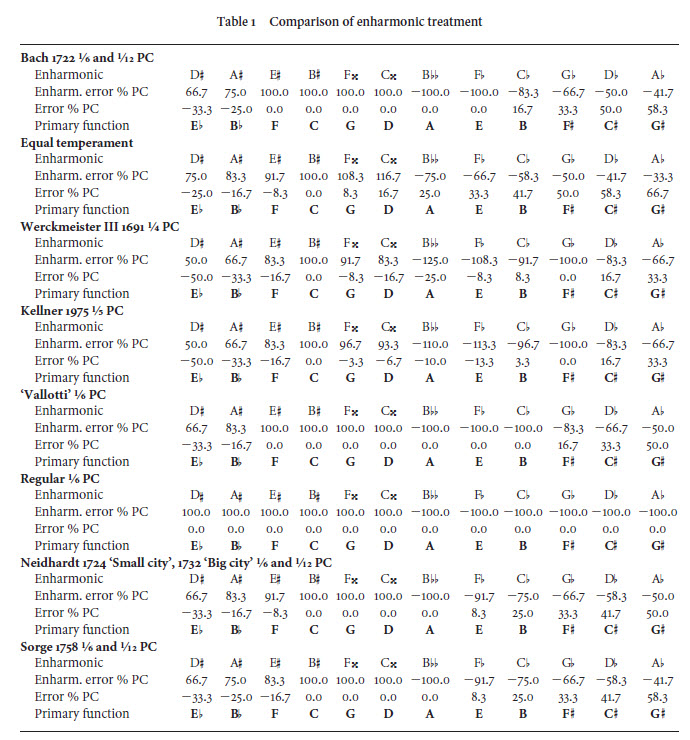
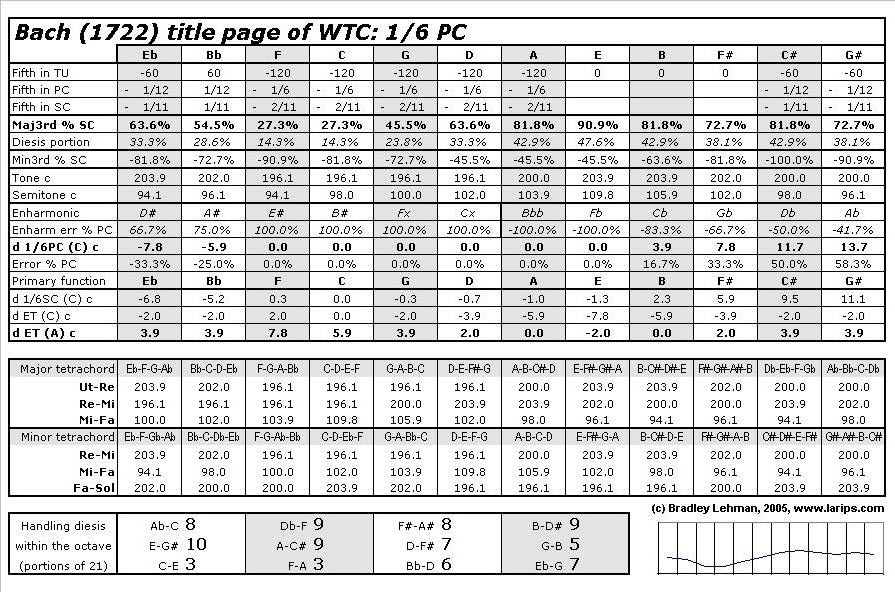
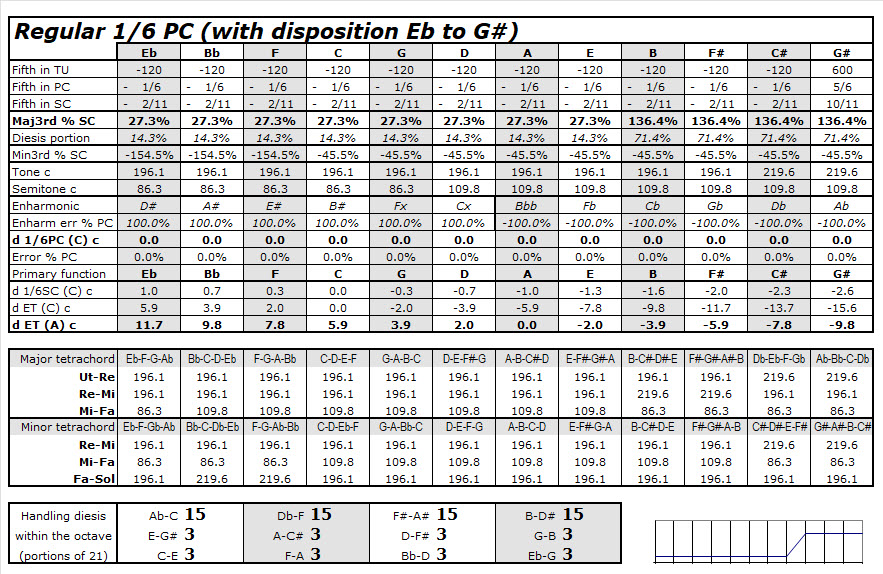
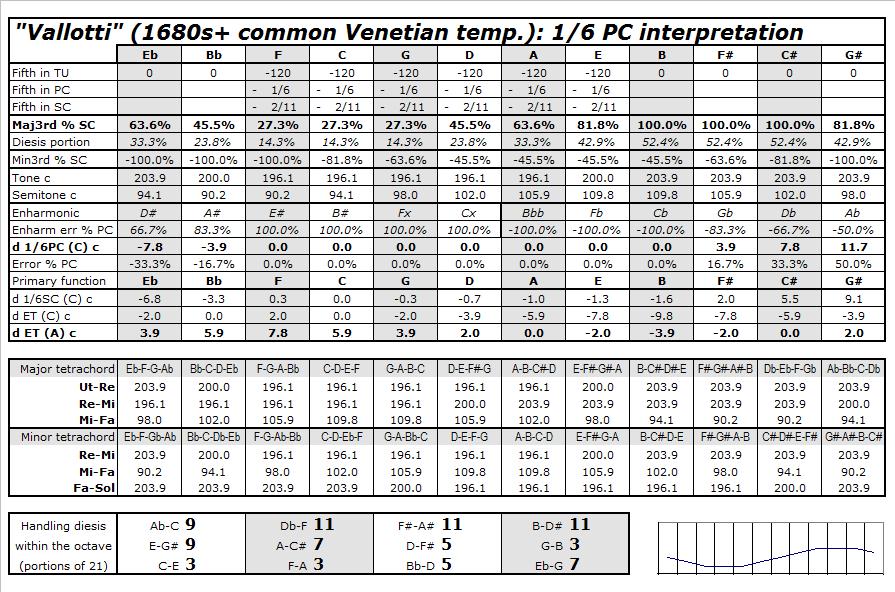
That is the crux of the enharmonic problems set up by the music. How do we tune so all of the various occurrences of Fa, Ti, Mi, and all the other diatonic notes will make sense in scales, and in any harmonies that are built from those scales?

The 2005 article included 44 tables (the three seen below, and 41 others) as part of its "Supplementary Data" files. For the printed sections of that article, there was space available for only this condensed table on page 215, as part of the "Enharmonics" section explaining it (214-218).

The rows of percentages are drawn from these analyses in the "Supplementary Data" set:

I drew data from the 41 other tables similarly. I explained the percentages within the available space. The background for all the percentage measurements is the row for "Regular 1/6 PC", the consistent tempering by 1/6 Pythagorean Comma (or, seeing it in another way, the 55-step division of the octave). If we tune a note such as Eb "purely" as Eb, it is 100% of a comma out of tune if we try to play that same pitch as D#. That D# is too sharp by that comma. If we tune a "pure" C# with 0 error, the Db has an error of -100%: the Db is a full comma too flat.

In these other temperaments that modify some of the notes against that background of regularity, I measured the compromises where these pitches are pushed up or down part of the way toward the other enharmonic note. I showed how these tuning errors (fragments of a comma) are handled differently from note to note. For example, when we have set up a compromise where the note G# is 58.3% of a comma out of tune (too sharp), the corresponding note Ab is the other -41.7% of a comma out of tune in the other direction (too flat). These enharmonic errors between sharps and flats are the reality that must be dealt with as compromises whenever we have keyboards with only 12 notes per octave. Any particular pitch might sound "better" when played as a sharp than as a flat, or vice versa, but it is usable either way...as long as we have controlled the transitions carefully enough, within the ways that scales really work.

In that section, I then showed that the temperaments that work well have their errors increase smoothly from note to note. The temperaments that don't work well (such as "Werckmeister III") move more haphazardly, as I explained. These measurements show why such temperaments sound crude. As I said with regard to such misshapen temperaments, "the misspelled notes simply stick out obtrusively, because their deviations from the 55-division skip across the set of notes rather than being well-organized outward from C."

Now, in 2022, I am attempting to explain this more clearly without expecting everyone to see it as percentages, or as numbers. We hear these pitches within the context of music. The notes either sound "in tune" enough (i.e., fitting into the scales where they are use), or they sound "out of tune". The numbers from 2005 are still correct, but again, they are only measuring phenomena that are not merely mathematical. The numbers only describe the musical shapes we can hear whenever the harpsichord's pitches are set deliberately a little bit too sharp, or a little bit too flat, so those pitches can be played as notes with different names. The music demands that flexibility of renaming the notes.

That is one of the reasons for the 2022 article, "The Notes Tell Us How to Tune": to explain all of this again with better emphasis on the scales and the hands-on compromises at a harpsichord...not the mathematical measurements that might have made it harder (rather than easier) for some readers to understand the enharmonic points.

So, we will give more attention now to Fa, Ti, Mi, and the way we handle them through scales and modulations. Set aside those percentages of comma errors, because we don't need them anymore to keep moving forward with this. Those numbers are all in the background.

When tuning and adjusting a harpsichord by ear, it is a process of listening to scales and harmonies, not doing anything with numbers. We can tune a harpsichord or tie a pair of shoes without measuring anything. We just have to get the shapes and the motions right.

The process is:

• Set up all the notes of the C major scale first, using regular 1/6 comma tempering (the naturals from the 55-division of the octave).
• Make B and the sharps slightly higher than they were supposed to be in that regular system.
• That is, each time we build the new note, we are making Ti of the major scale go a little bit higher, as more of a leading tone up to Do.
• We are also checking that our raised Ti also sounds good enough as a Mi, so it is not getting too high.
• That is, build B from E, checking it with G. Build F# from B, checking it with D. Build C# from F#, checking it with A. Build G# from C#, checking it with E. Build D# from G#, checking it with B. Build A# from D#, checking it with F#.
• Notice that we have been working on the same note that is the next sharp being added to a key signature, in turn around the spiral of fifths. F#, C#, G#, D#, A#, [E#, B#].
• Part of the reason for raising all these Ti pitches is that they also must serve as Do and Sol soon (after several more steps). If B and the sharps would stay too low, we will find soon that the flat scales with their own Mi and Fa will not work well enough. Furthermore, D# sounds bad if B is too low, and D# is needed frequently for keys as simple as A minor and E minor.
• When we get to the end with A#, we have built 12 different pitches. Those are the original F-C-G-D-A-E making the C major scale of C, D, E, F, G, A; and then we built B-F#-C#-G#-D#-A# treating each of those as a new Ti, checking them also as Mi.
• We already have F from the beginning. We already know that it makes a terrific Fa above the Do of C. Play the F as if it were E#, and be sure it makes a good enough Sol above A#, and a good enough Mi above C#.
• Check everything backward from the A# ending point, using Fa. The A#, played as if it were Bb, makes a good enough Fa for F major. (Play: Fa, Mi, Re, Do, Re, Mi, Fa, Sol.) The D#, played as if it were Eb, makes a good enough Fa for Bb major. The G#, played as if it were Ab, makes a good enough Fa for Eb major. (...) The E, played as if it were Fb, makes a good enough Fa for Cb major.
• Notice that we have been backward-checking these Fa flats down to Do in the same order that flats get added to a key signature: Bb, Eb, Ab, Db, Gb, Cb, Gb.
• As if by magic, we can now play the B major scale, the Eb major scale, the C# major scale, our original 55-division C major scale, and everything works.
• We have six pure naturals ("pure" to the 55-division), and the other six compromised pitches generated by building Ti and then back-checking through Fa. We can play music in every major scale or every minor scale, without having to worry that any note will ever sound wrong.

Those pure naturals and the other compromises are like this, looking back at the percentage numbers from 2005:

[For more on the 55-division and 1/6 comma, read the bigger articles....]

---

(More illustrations, and their explanations will be here soon....)

(The remaining parts of the text are to be posted in December 2022 with everything hyperlinked; drafted 2021 as a section of a longer article, "The Notes Tell Us How to Tune")

See also the presentation of test pieces surveying Bach's keyboard music.

Return...