LaripS.com, © Bradley Lehman, 2005-22, all rights reserved. All musical/historical analysis here on the LaripS.com web site is the personal opinion of the author, as a researcher of historical temperaments and a performer of Bach's music.
Comparisons with other temperamentsSeveral of the supplementary files available from Oxford's web site explicate and thoroughly analyze the temperaments summarized in the following chart.This comparative material was submitted as an appendix within my original manuscript. During the editorial process (splitting the printed article into two halves, with limited space in the printed journal) this portion became a web-only supplement of the February half. It includes 50 additional pages of mathematical analysis along this line.
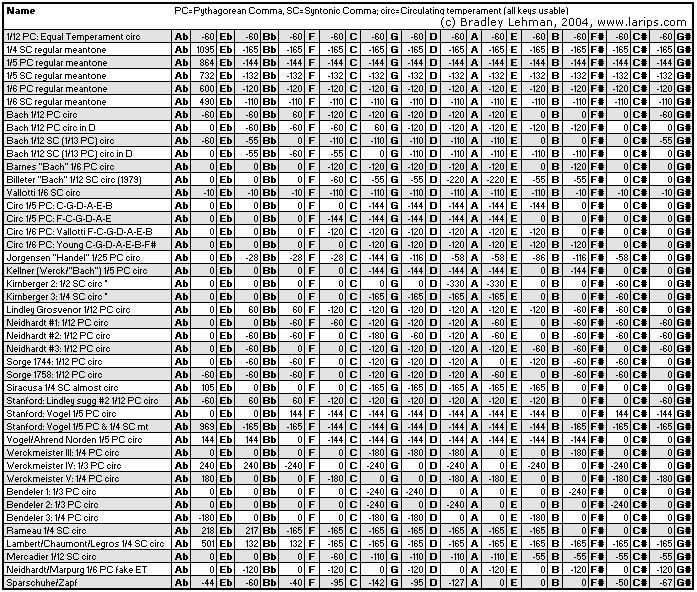
Comparison of Bach's temperament with other representative temperaments. The focus of the present article is on the temperament here labeled "Bach 1/12 PC circ". For this comparison, the unit of measurement is the "Temperament Units" system devised by organ-builder John Brombaugh. It is a logarithmic scale assigning 720 microscopic portions to the Pythagorean comma. The syntonic comma then works out to 660 TU, the schisma (difference between them) 60. All of these numbers are easy to work with on paper, divisible by 3, 4, 5, 6, and 12: the fractions used in most descriptions of theoretical temperaments. The TU system therefore allows a theorist or player to work almost exclusively with integers in sorting out the concepts of keyboard tuning. Each row of the chart sums to -720: the distribution of the PC around the circle. To find the quality of the major thirds, sum the four intervening fifths and add 660, then divide the result by 660. For example, in Barnes's temperament the third Eb-G is 420/660 or 63.6% sharp of pure: the same amount that all the major thirds of equal temperament are (and therefore also the average of all twelve thirds, in every temperament).
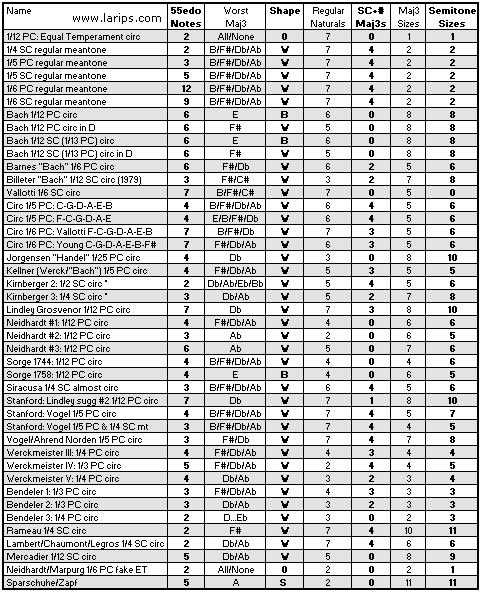
Further details and annotations are of course in the Oxford web supplements. See also my introductory presentation of the "Temperament Units" metric, and both pages of the Frequently Asked Questions. A comparison with regular 1/6 comma and with equal temperament is the graph shown on the Enharmonic handling page. And see the analytical survey of other "Bach" temperaments since 1966.
Neidhardt clarifications..."Neidhardt #1" here is the 1724 "Kleine Stadt" recommendation, and promoted by him to "Grosse Stadt" in 1732. "Neidhardt #2" here is the 1724 "Grosse Stadt" recommendation. "Neidhardt #3" here is the 1724 "Dorf" recommendation, and promoted by him to "Kleine Stadt" in 1732. Note: The intervallic pattern of "Neidhardt #3" is incorrect in the above charts, at the note G#; likewise the "Neidhardt #2" is incorrect at the note G. See the errata page for clarification, and the correct versions of these. I had used these three Neidhardt temperaments in the sequence and details they are given in New Grove 2nd edition (2001), which unfortunately has printed errors in it!
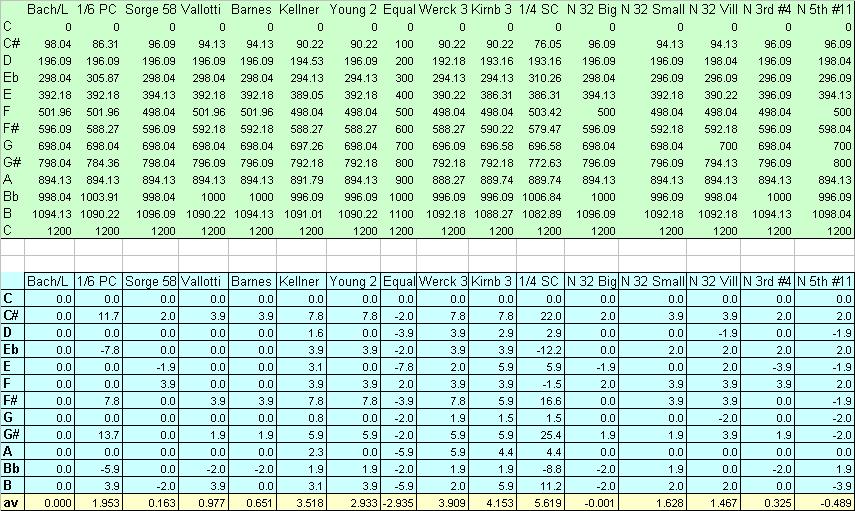
Converting from some other temperament to the Bach?The following tables show the cent values of all twelve notes in the octave, holding C as constant.The sample temperaments shown here are: Bach/Lehman, regular 1/6 Pythagorean comma (like "Silbermann"), Sorge's from 1758, "Vallotti" (which was probably already in practice in the 17th century, long before Vallotti himself, since it's so easy and symmetrical as an "ordinary" practice...), Barnes and Kellner (each from the 1970s), Young's #2 (1799/1800), equal temperament, Werckmeister III (1680s-91), "Kirnberger 3" (which was only something he mentioned offhand in a letter), regular 1/4 comma meantone, and five temperaments from Neidhardt's 21 temperaments of 1732 (Big City, Small City, Village, 3rd-circle #4, and 5th-circle #11).
The blue section at the bottom shows the offsets, to the nearest 1/10th cent, with the Bach/Lehman position taken as 0 for each of the twelve notes. For example, if converting from some harpsichord (or organ or piano) that is already in regular 1/6 comma, six of the notes stay where they are. The C# needs to be raised 11.7 cents; F# raised 7.8; G# raised 13.7; B raised 3.9; Eb lowered 7.8; and Bb lowered 5.9. In some of these it makes a difference if one wants to preserve a constant A, or some other average point (for overall tension/pitch of the instrument), instead of C. Several examples illustrate these concepts:
 |
v Introduction v Articles v FAQ v Practice > Theory - Measurements * Comparisons - Other "Bach" - [Extra]ordinary - Regular/Mean - Enharmonics - Cube puzzle - Geometric 5ths - TU & Schismas - Fa Ti Modulation v History v Etc v Recordings |