Variational Statement
We now mix the ingredients. Recall that the driving force is defined as the reduction of the free energy of the composite when an atom relocates by unit distance. Translating this definition into a mathematical description, we have
|
|
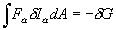
(9) |
The two vector fields, u and I, are basic kinematic variables; they vary independently, subject to no constraint. Mass transport dissipates energy, but elastic deformation does not. The variational statement embodies these considerations.
Calculate 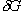 using previous equations, giving
|
|
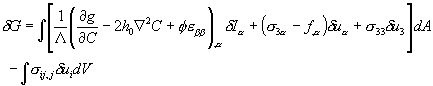
(10) |
where  .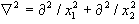
Now compare (9) and (10). The free energy variation with the mass relocation gives the expression for the driving force for diffusion
|
|
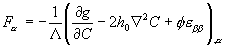
(11) |
because elastic deformation does not dissipate energy, the free energy variation with the elastic displacement vanishes, leading to
|
|
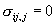
(12) |
in the bulk and
|
|
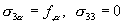
(13) |
on the surface. Equation (12) recovers the equilibrium equation in the elasticity theory. Equation (13) has a straightforward interpretation. Recall that the surface stress is the resultant force (per unit length) of the residual stress in the surface layers. Force balance equates the gradient of the surface stress to the tangential traction. Equation (13) sets the boundary conditions of the elastic field in the substrate.
Observe that the concentration-dependent surface stress varies with both fields u and I. Consequently, the two fields are coupled, as will be clear shortly. The surface stress enters the diffusion driving force (11), and causes the concentration field to change. Once concentration field changes, the surface stress changes and, through the boundary conditions (13), changes the elastic field in the substrate.
The elastic field in a half space due to a tangential point force acting on the surface was solved by Cerruti. A linear superposition gives the field due to distributed traction on the surface. Only the expression 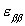 enters the diffusion driving force. The Cerruti solution gives
|
|
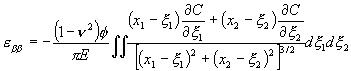
(14) |
The integration extends over the entire surface.
A combination of (7), (8) and (11) leads to a diffusion equation
|
|
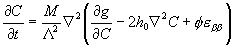
(15) |
|
