Energetics
Let the reference state for the free energy be atoms in three unstrained, infinite, pure crystals of A-atoms, B-atoms and S-atoms. When atoms are taken from the reference state to form the epilayer-substrate composite, the free energy changes, due to the entropy of mixing, the misfits among the three kinds of atoms, and the presence of the free space. In addition, the misfits can induce an elastic field in the substrate. Let G be the free energy of the entire composite relative to the same number of atoms in the reference state. For an epilayer only one atom thick, we cannot attribute the free energy to individual kinds of misfit. Instead, we lump the epilayer and the adjacent monolayers of the substrate into a single superficial object, and specify its free energy. The free energy of the composite consists of two parts: the bulk and the surface, namely
|

|
(1) |
The first integral extends over the volume of the entire system, W being the elastic energy per unit volume. The second integral extends over the surface area, G being the surface energy per unit area. Both the volume and the surface are measured in the unstrained substrate. As a convention, we extend the value of the substrate elastic energy W all the way into the superficial object. Consequently, the surface energy G is the excess free energy in the superficial object in addition to the value of the substrate elastic energy. The convention follows the one that defines the surface energy for a one-component solid.
The elastic energy per unit volume, W, takes the usual form, being quadratic in the strain tensor,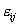 (A Latin subscript runs from 1 to 3). Assume that the substrate is isotropic, with Young’s modulus E and Poisson’s ratio n. The elastic energy density function is (A Latin subscript runs from 1 to 3). Assume that the substrate is isotropic, with Young’s modulus E and Poisson’s ratio n. The elastic energy density function is
|
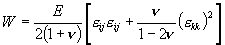
|
(2) |
The stresses 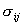 are the differential coefficients, namely, are the differential coefficients, namely, 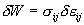 . Let . Let 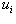 be the displacement vector of a material particle relative to the reference state. The strain tensor be the displacement vector of a material particle relative to the reference state. The strain tensor 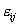 relates to the displacement gradient tensor in the usual way: relates to the displacement gradient tensor in the usual way:
|
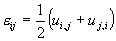
|
(3) |
The surface energy per unit area, G, takes an unusual from, as we now explain. Assume that G is a function of the concentration C, the concentration gradient 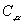 , and the strain in the surface, , and the strain in the surface, 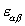 (A Greek subscript runs from 1 to 2). Expend the function (A Greek subscript runs from 1 to 2). Expend the function 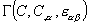 to the leading order terms in the concentration gradient to the leading order terms in the concentration gradient 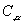 and the strain and the strain 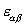 : :
|
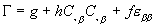
|
(4) |
where g, f and h are all functions of the concentration C. For simplicity, we have assumed isotropy in the plane of the surface. Please refer to our papers for anisotropic case. The leading order term in the concentration gradient is quadratic because, by symmetry, the term linear in the concentration gradient does not affect the surface energy. We have neglected terms quadratic in the displacement gradient tensor, which relate to the excess in the elastic constants of the epilayer relative to the substrate.
Assume that the epilayer is a regular solution, so that the function takes the form
|
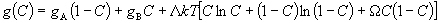
|
(5) |
The 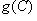 term has already been discussed (see Ideas). Its function is mainly responsible for phase separation; it favors neither coarsening nor refining. term has already been discussed (see Ideas). Its function is mainly responsible for phase separation; it favors neither coarsening nor refining.
Assume 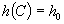 is a material constant. Any nonuniformity in the concentration field by itself increases the free energy G. Consequently, the second term in (4) is taken to represent the phase boundary energy; the term drives phase coarsening. The first two terms in (4) are analogous to those in the model of bulk phase separation of Cahn and Hilliard. The model represents a phase boundary by a concentration gradient field. is a material constant. Any nonuniformity in the concentration field by itself increases the free energy G. Consequently, the second term in (4) is taken to represent the phase boundary energy; the term drives phase coarsening. The first two terms in (4) are analogous to those in the model of bulk phase separation of Cahn and Hilliard. The model represents a phase boundary by a concentration gradient field.
Now look at the last term in (4), where 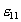 and and 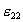 are the strains in the surface. By definition, f is the change in the surface energy per unit strain. Consequently, f represents the residual stress in the superficial object. More precisely, it is the resultant force per unit length. The quantity f is known as the surface stress. Assume that the surface stress is a linear function of the concentration, are the strains in the surface. By definition, f is the change in the surface energy per unit strain. Consequently, f represents the residual stress in the superficial object. More precisely, it is the resultant force per unit length. The quantity f is known as the surface stress. Assume that the surface stress is a linear function of the concentration,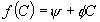 . Ibach et al. have reviewed the experimental information on this function. . Ibach et al. have reviewed the experimental information on this function.
|

