ME 574 PROJECT

An Axisymmetric Model for Pore-Grain Boundary Separation

 

Home

Introduction

Modeling

Numerical Methods

Results &  Conclusion

Informations

 
Mathmatical Modeling

A pore located on a grain boundary. The pore size is characterized by r0, the radius of a sphere that has the same volume as the pore. The diameter of the axisymmetric unit is 2R, which represents pore spacing. It is assumed that the pore spacing is equal to the grain size for simplicity. A force fb at the outside edge of the interface represents the force on the interface by the grain boundaries. The pore moves by atomic diffusion on its surface, and the interface moves as atoms detach from grain II and attach to grain I.


   


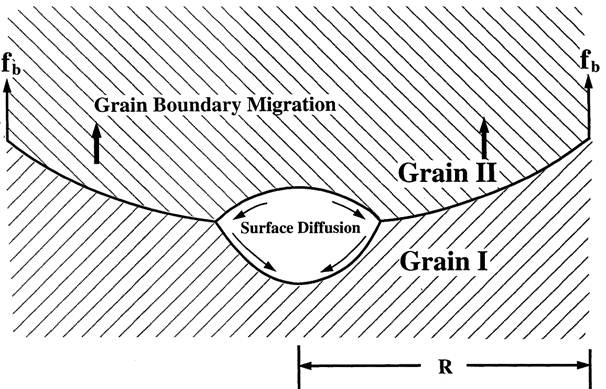    Figure 1. An 2D axisymmetric model.

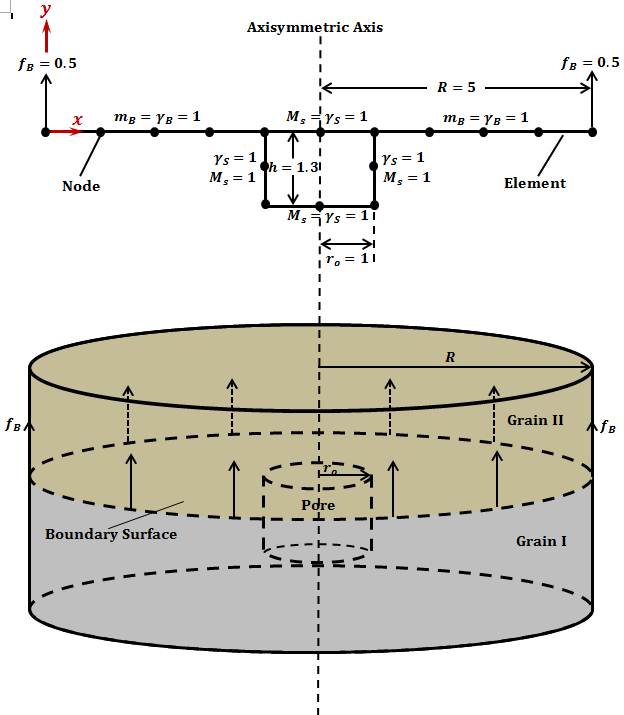              Figure 2. An 3D axisymmetric model.
                   

Weak Statement
For a system of surfaces and grain boundaries, the total free evergy is

G = gSAS + gBAB,

where gS is the surface energy density, gB is the grain boundary energy density, AS is the area of the surface, AB and  the total grain boundary area.

After following methmatical procedure described in Yu et al., the virtual motion of the grain boundaries and surfaces change the total free energy by dG.
 Finite Element Method



        Figure 3.  An axisymmetric element in three dimensions (a) and in a plane (b).


Figure 3 shows one element with nodes (x1, y1) and (x2, y2).  The generalized velocities are


On the element, interpolate the virtual displacement and actual velocity linearly:


with the interpolation coefficients being

Interpolate the virtual mass displacement and actual mass flux quadratically:
with the interpolation coefficients being
 
 H matrix

The FEM implementation of weak statement has been carried out for both 2D formulation and axisymmetric 3D formulation.

For both cases, the viscosity matrix H on the grain boundary is a 4×4 matrix, and on the pore surface is 7×7 matrix.

          1.      2D formulation

On the grain boundary, the weak statement becomes:

Where the viscosity matrix H is a 4×4 symmetric matrix calculated from:  , which gives:

On the pore surface the weak statement becomes:

This will generate H as a 7×7 symmetric matrix. A Matlab code is written to automatically calculate the components of this viscosity matrix.

 

           2.      3D formulation

The derivation of the viscosity matrices for 3D axisymmetric case has the same method as in 2D formulation. However, the integration now is not the integration along the line. It becomes the integration over the area the rotated surface. For one element the surface area is: . Hence, after integrating, the 4×4 viscosity matrix on the grain boundary has the following forms:

The difference can be seen when comparing this matrix and the one in 2D case.

The 7×7 symmetric viscosity matrix is also generated automatically by a Matlab code.

 

The force vector for each element is derived from the right hand side of the weak statement. The free energy reduction of the element is:

                                       

Using the line element for 2D formulation, and axisymmetric  element for 3D formulation lead to two the following corresponding force elements:

           1.      2D formulation

                   

           2.      3D formulation

 There are only driving forces associated with the movement of the coordinates. No driving forces are associated with .

 
 
 Assembling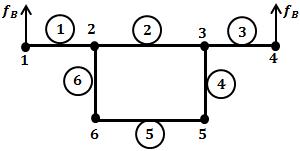


Figure 4. Model with minimum possible nodes and elements.




In the preceding section, we showed how to obtain the local H and f matrices for each node on the grain boundaries and along the pore surfaces. In this section, we need to assemble the local H and f matrices to global ones so as to obtain the velocity of each node.

In order to better understand how the assembling process looks like in the present problem, we start with the model containing the minimum possible nodes and elements, as shown in the Figure 4. Nodes 2,3 and 1,4 are called triple junctions and boundary nodes, respectively. In the following, the global H and f matrices are given by

Nodes 1 and 2 (element 1)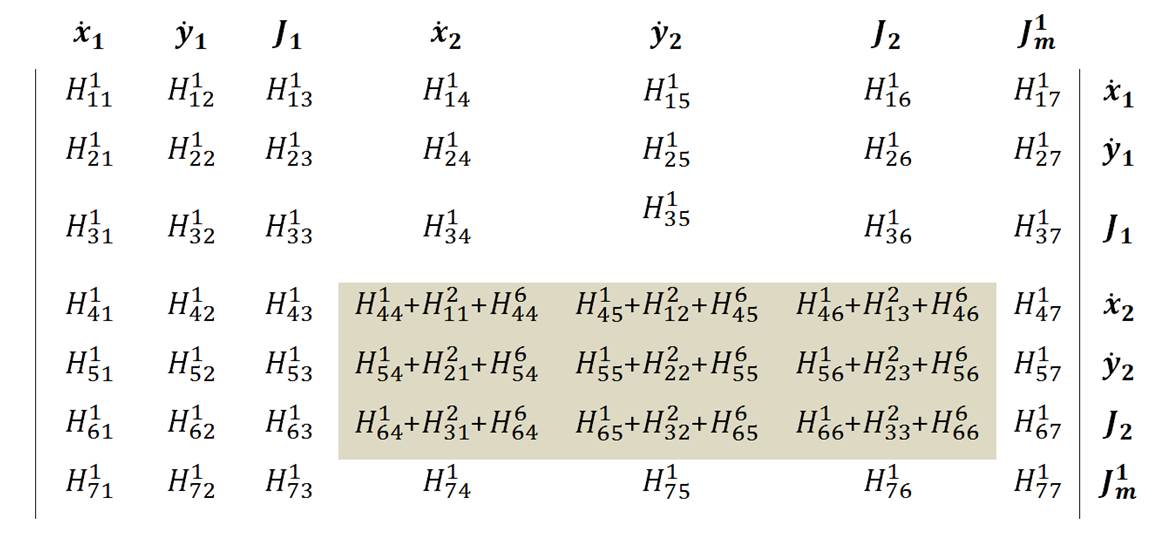



Nodes 2 and 3 (element 2)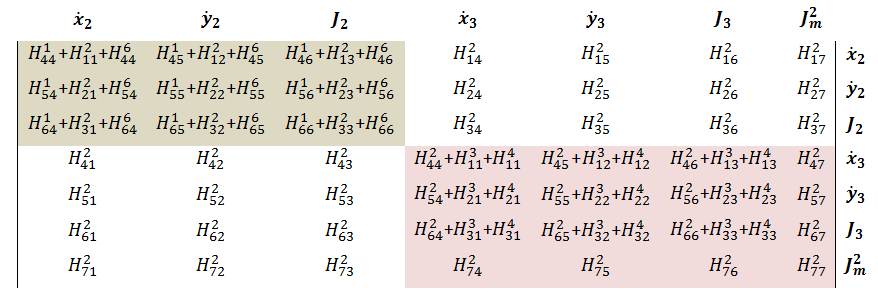



Nodes 3 and 4 (element 3)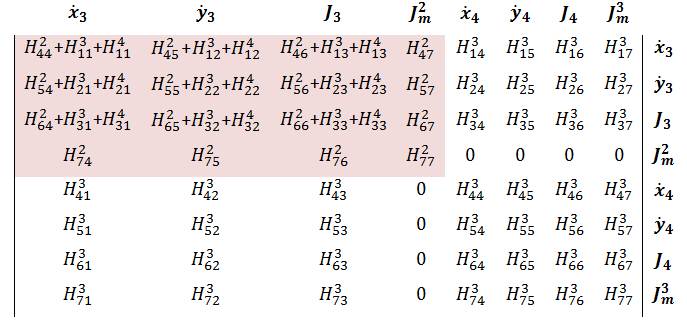

Nodes 3 and 5 (element 4)


Nodes 5 and 6 (element 5)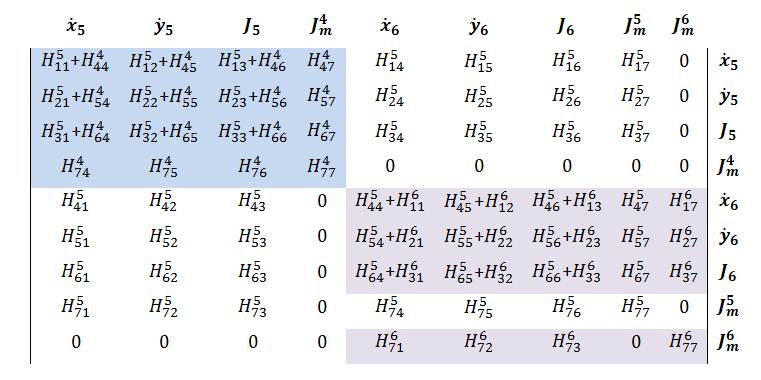

Nodes 6 and 2 (element 6)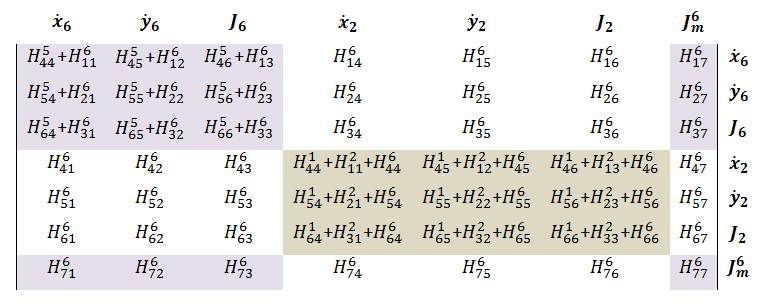


Big picture of the global H matrix is shown below. Off diagonal components is due to the triple junctions and the closed contour.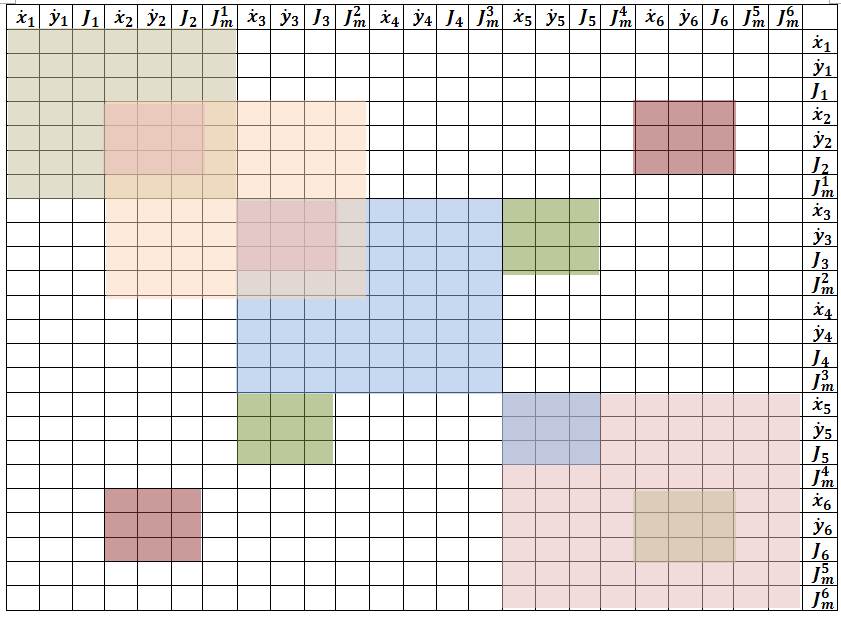


The global f matrix can be given by


Inserting the above global H and f matrices into the following equation, a set of nonlinear ordinary differential equations governing the generalized coordinates as a function of time is obtained.

From the above equation, we can see that the velocity direction usually differs from the direction of the generalized force, i.e., gradient of free energy. The above equation is integrated numerically (i.e., Fourth-Order Runge-Kutta method) to evolve the surfaces.

Boundary conditions

At the boundry nodes 1 and 4, the velocity in the horizental direction is set to be zero. It can be done by adding a very large number to the corresponding H components of the boundary nodes. In addition, the external boundary force fB needs to be added to the corresponding f components of the boundary nodes, as shown in the preceding section.
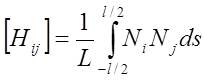
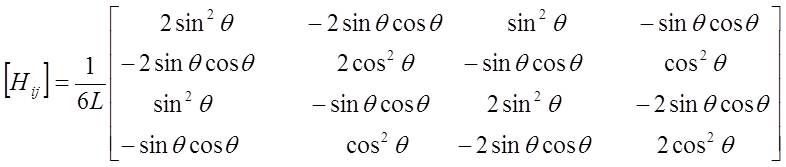
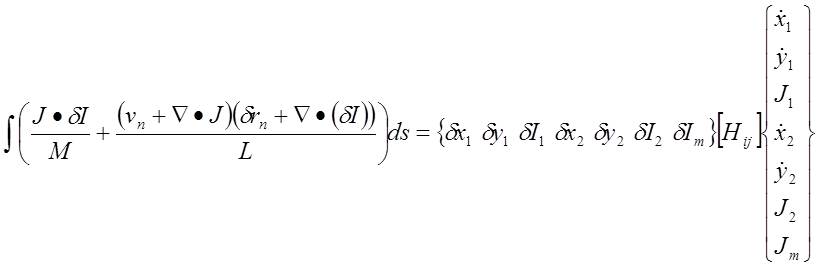
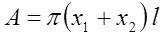
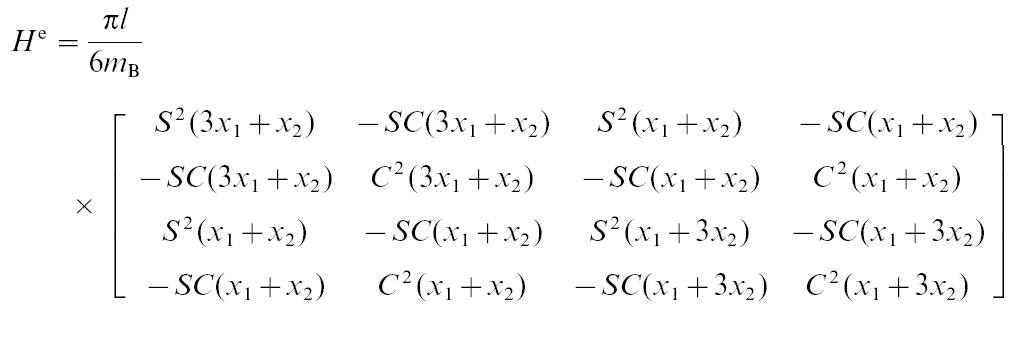
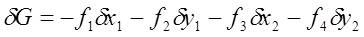
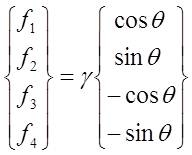
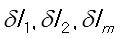