Hiperbolikus, parabolikus és elliptikus egyenletek

A gázok és folyadékok kölcsönható részecskébõl - atomokból, molekulákból - állnak. Az egyes részecskék mozgásának leírása a részecskék nagy száma miatt (tipikusan $10^{23}$) mind analitikusan mind számítógépes modellezéssel megoldhatatlanul bonyolult probléma. Éppen ezért a folytonos közeget néhány dinamikai és termodinamikai mennyiséggel - a $\mathbf{v}$ átlagsebességgel, $\rho$ sûrûséggel, $p$ nyomással, stb. - jellemezzük és ezekre vonatkozóan próbálunk meg zárt egyenletrendszert felírni.

Általában az alapvetõ megmaradási törvényekbõl kiindulva tetszõleges térfogatra vonatkozó integrálegyenleteket vezetünk le, majd ezeket az integrálegyenleteket átírjuk parciális differenciálegyenletekre. Például a tömegmegmaradás egyenlete integrális formában így írható fel:

$$\frac{d}{dt}\int_V \rho\,dV = - \int_{\partial V} \rho \mathbf{v}\cdot d\mathbf{A}$$ (1)

ahol a $V$ térfogat zárt felületét $\partial V$-vel, az infinitezimális térfogat elemet $dV$-vel, az infinitezimális felület elem kifelé mutató normál vektorát pedig $d\mathbf{A}$-val jelöltük. Az egyenlet egyszerûen annyit állít, hogy a térfogatba zárt össztömeg a felületen áthaladó normális irányú tömegfluxus hatására változik meg. Ez az integrálegyenlet térben folytonos sûrûség és sebesség eloszlások esetén átírható egy parciális differenciál egyenletre:

$$\frac{\partial \rho}{\partial t} + \mbox{div}(\rho \mathbf{v}) = 0$$ (2)

amit általában a kontinuitási egyenletnek szoktunk nevezni.

Mivel analitikusan a parciális differenciál egyenletek (PDE-k) sokkal jobban kezelhetõk mint az integrál egyenletek, ezért általában a folytonos közegeket klasszikusan PDE-k segítségével írjuk le. Mint a késõbbiekben látni fogjuk, a számítógépes modell esetében mind az integrál, mind a differenciál egyenletbõl kiindulhatunk. Mielõtt azonban ezt megtennénk, fontos röviden áttekinteni a PDE-k osztályozását, ugyanis az egyes osztályok modellezése más-más módszert igényel. Itt hely hiányában a szigorú matematikai osztályozás helyett csak a fizikai tulajdonságok alapján való osztályozásra térünk ki.

Ábra 1.: A három PDE osztály téridõ diagramja. A satírozott rész függ a ponttal jelölt eseménytõl. Az elliptikus esetben mindkét koordináta tér jellegû.

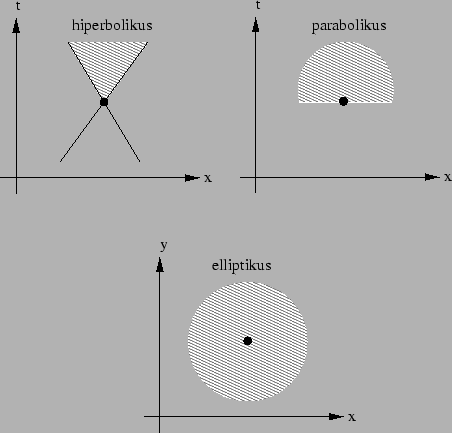A hiperbolikus egyenletekkel leírt rendszerekben egy adott idõbeli és térbeli pontban a közeg állapotának a megváltozása egy késóbbi idõpontban csak egy véges térrészben fejti ki hatását. Egy téridõ diagrammon (lásd a 1. ábra bal felsõ részét) ezt egy kúppal szemléltethetjük, melynek csúcsa a pontszerû változásnál található, és a változás következménye a kúpon belül marad. Más szóval az információ véges sebességgel terjed. Hiperbolikus egyenletekre példák: a vákum elektrodinamikáját leíró Maxwell egyenletek, az összenyomható és elhanyagolható viszkozitású gázokat leíró Euler egyenletek, vagy a mágneses térrel kölcsönható elhanyagolható fajlagos ellenállású plazmákat leíró ideális magnetohidrodinamikai egyenletek. Szintén a hiperbolikus rendszerekre jellemzõ, hogy a véges sebességgel terjedõ síkhullámok nem csillapodnak, valamint határesetben szakadási felületekkel rendelkezõ megoldások is léteznek.

A parabolikus egyenletekkel leírt rendszerekben a pontszerû változás hatása egy félsíkra terjed ki (lásd a 1. ábra jobb felsõ részét), azaz az információ végtelen gyorsan terjed. Ugyanakkor maga a hatás általában exponenciálisan csökken a távolsággal. A parabolikus egyenletek disszipatív, diffúzív rendszereket írnak le: a viszkózus gázokra vonatkozó Navier-Stokes egyenletek, a véges vezetõképességû plazmákra vonatkozó rezisztív magnetohidrodinamikai egyenletek, vagy a hõterjedést leíró diffúziós egyenlet. Érdemes megemlíteni, hogy a fizikai valóságban természetesen az információ, így például a hõmérsékletváltozás, véges sebességgel terjed, és csak a fizikai rendszert közelítõen leíró PDE-k viselkednek parabolikusan. A közelítés azonban rendkívül jó, mivel a fizikai hõterjedés valóban sokkal gyorsabb mint az egyéb jellemzõ sebességek, másrészt a távolsággal a hatás nagyon gyorsan csillapodik, így nincs különösebb jelentõsége a végtelen gyors információ terjedésnek a matematikai modellben. A parabolikus egyenletek által leírt rendszerekben a síkhullámok amplitúdója csökken, és a kezdetben éles szakadási felületek kiszélesednek, folytonossá válnak.

Az elliptikus egyenletekben nem szerepel idõszerû változó, nincs kitüntetett terjedési irány, így a megoldás csak az összes határfeltételek együttes ismeretében adható meg (lásd a 1. ábra alsó részét). Példaként említhetjük a gravitációs potenciál és a tömegsûrûség kapcsolatát megadó Poisson egyenletet, vagy a folytonos közeg stacionárius áramlását leíró egyensúlyi egyenleteket. Mivel az elliptikus problémák megoldása gyökeresen más numerikus módszereket igényel mint a hiperbolikus és parabolikus eseteké, a továbbiakban csak az utóbbiakról lesz szó.