


Next: Feladat: folytonos kezdeti feltétel
Up: Gáz és plazma dinamika
Previous: Hiperbolikus, parabolikus és elliptikus
Tartalomjegyzék
Diszkretizáció
A számítógép nem tud végtelen sok folytonosan változó mennyiséget
kezelni, ezért a numerikus modell szükségszerûen véges
sok változóval közelíti meg a valóságot, illetve annak
matematikai modelljét. Magukat a változókat általában lebegõpontos
valós (esetleg komplex) számok ábrázolják, melyek szintén véges
pontosságúak, általában 6 12 tizedes jegyet tartalmaznak.
Az elsõ közelítést diszkretizációnak nevezzük, mely
diszkretizációs hibát okoz. Általában minél több változót
használunk a számítógépes modellben, annál kisebb a diszkretizációs
hiba. A véges pontosságú számábrázolás okozta kerekítési hiba
általában nagyságrendekkel kisebb a diszkretizációs hibánál.
12 tizedes jegyet tartalmaznak.
Az elsõ közelítést diszkretizációnak nevezzük, mely
diszkretizációs hibát okoz. Általában minél több változót
használunk a számítógépes modellben, annál kisebb a diszkretizációs
hiba. A véges pontosságú számábrázolás okozta kerekítési hiba
általában nagyságrendekkel kisebb a diszkretizációs hibánál.
Tekintsük a (2) kontinuitási egyenletet egy térbeli
dimenzióban:
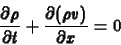 |
(3) |
és próbáljuk meg diszkretizálni. Az 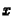 tér változót helyettesítsük
az
tér változót helyettesítsük
az 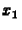 ,
, 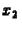 ,
, 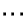 ,
, 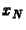 diszkrét változókkal, míg az
idõt a
diszkrét változókkal, míg az
idõt a 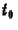 ,
, 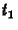 ,
, 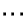 változókkal reprezentáljuk.
Az egyszerûség kedvéért tekintsünk egy szabályos tér rácsot,
azaz
változókkal reprezentáljuk.
Az egyszerûség kedvéért tekintsünk egy szabályos tér rácsot,
azaz
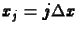 , ahol
, ahol 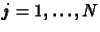 és
és 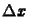 a rácsállandó,
valamint legyen a
a rácsállandó,
valamint legyen a 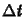 idõlépés is konstans, azaz
idõlépés is konstans, azaz
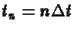 ,
ahol
,
ahol 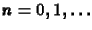 .
A sûrûséget egy adott
.
A sûrûséget egy adott 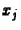 rácspontban és
rácspontban és 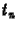 idõpillanatban a
idõpillanatban a
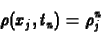 |
(4) |
mennyiség reprezentálja. A felsõ index nem hatványozást jelent,
hanem ez a szokásos jelölése az idõ szerinti indexnek.
A kontinuitási egyenlet lényegében hiperbolikusan
viselkedik, ugyanis egy sûrûségperturbáció véges 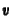 sebességgel
terjed. Egy hiperbolikus egyenletet az adott kezdeti feltételek,
azaz
sebességgel
terjed. Egy hiperbolikus egyenletet az adott kezdeti feltételek,
azaz
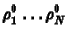 változók ismeretében lehet megoldani.
A kezdeti feltételt általában ki kell egészíteni a
határfeltételekkel, azaz
változók ismeretében lehet megoldani.
A kezdeti feltételt általában ki kell egészíteni a
határfeltételekkel, azaz 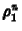 -t és/vagy
-t és/vagy 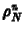 -t meg
kell adni. Jelen esetben azon az oldalon kell határfeltételt megadni,
ahol a
-t meg
kell adni. Jelen esetben azon az oldalon kell határfeltételt megadni,
ahol a 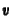 sebesség befelé mutat.
Az egyszerûség kedveért legyen
sebesség befelé mutat.
Az egyszerûség kedveért legyen 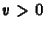 térben és idõben konstans.
térben és idõben konstans.
Miután a változókat diszkretizáltuk, a következõ lépés a
(3) parciális differenciálegyenlet átírása ezekre
a változókra, azaz az egyenlet diszkretizálása. Ez a lépés
egyáltalán nem triviális, hiszen a folytonos PDE-t végtelen
sokféleképpen lehet diszkrét algebrai egyenletekkel közelíteni.
Ezek a közelítések, azaz diszkretizációk mind más-más pontossággal
és stabilitási tulajdonsággal rendelkeznek, illetve különbözõ
mennyiségû számítási illetve programozási munkát igényelnek.
Tekintsük most az egyik legegyszerûbb diszkretizációt, amit
különösebb levezetés nélkül, lényegében intuitív módon
fel lehet írni. Közelítsük a 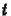 és
és 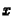 szerinti deriváltakat
a
szerinti deriváltakat
a 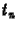 ,
, 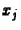 téridõ pontban egyszerû differenciákkal:
téridõ pontban egyszerû differenciákkal:
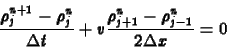 |
(5) |
ahol
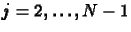 és
és 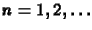 . Mint látható az idõderiváltat
egy féloldalas, míg a térderiváltat egy szimmetrikus differencia
formulával közelítettük. Az idõderivált ilyen felírása célszerûnek
látszik, hiszen így a
. Mint látható az idõderiváltat
egy féloldalas, míg a térderiváltat egy szimmetrikus differencia
formulával közelítettük. Az idõderivált ilyen felírása célszerûnek
látszik, hiszen így a 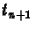 idõhöz tartozó megoldás közvetlenül
kifejezhetõ az
idõhöz tartozó megoldás közvetlenül
kifejezhetõ az 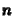 -dik lépésbõl:
-dik lépésbõl:
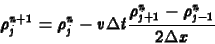 |
(6) |
A fenti diszkretizációt FTCS-nek szokás nevezni, ami az angol
,,forward in time centered in space'' (idõben elõre, térben centrális)
kifejezésbõl származik.
Alfejezetek



Next: Feladat: folytonos kezdeti feltétel
Up: Gáz és plazma dinamika
Previous: Hiperbolikus, parabolikus és elliptikus
Tartalomjegyzék
Gabor Toth
2000-09-04
![]() 12 tizedes jegyet tartalmaznak.
Az elsõ közelítést diszkretizációnak nevezzük, mely
diszkretizációs hibát okoz. Általában minél több változót
használunk a számítógépes modellben, annál kisebb a diszkretizációs
hiba. A véges pontosságú számábrázolás okozta kerekítési hiba
általában nagyságrendekkel kisebb a diszkretizációs hibánál.
12 tizedes jegyet tartalmaznak.
Az elsõ közelítést diszkretizációnak nevezzük, mely
diszkretizációs hibát okoz. Általában minél több változót
használunk a számítógépes modellben, annál kisebb a diszkretizációs
hiba. A véges pontosságú számábrázolás okozta kerekítési hiba
általában nagyságrendekkel kisebb a diszkretizációs hibánál.
![]() és
és ![]() szerinti deriváltakat
a
szerinti deriváltakat
a ![]() ,
, ![]() téridõ pontban egyszerû differenciákkal:
téridõ pontban egyszerû differenciákkal: