Mindeddig a meglehetõsen triviális kontinuitási egyenlettel
foglalkoztunk. Térjünk most át az összenyomható ideális gázok
dinamikáját leíró Euler egyenletekre. A kontinuitási
egyenletet a
![]() momentum és az
momentum és az ![]() energia sûrûségek megmaradási
egyenletei egészítik ki:
energia sûrûségek megmaradási
egyenletei egészítik ki:
Az Euler egyenletek hiperbolikus, nem lineáris PDE rendszert alkotnak.
Ezek megoldására a konvekciós egyenletnél bevált módszerek
valamennyien alkalmazhatóak. Újdonság azonban, hogy az információ
most már két különbözõ módon is terjedhet: hang illetve entrópia
hullámként. A hanghullám sebességét a ![]() konstans sûrûség,
konstans sûrûség,
![]() nyomás, és
nyomás, és ![]() sebesség értékek körül linearizált
egy dimenziós Euler egyenlet rendszerbõl lehet meghatározni.
Az eredmény két hullám megoldás, melyek sebességének abszolútértéke
sebesség értékek körül linearizált
egy dimenziós Euler egyenlet rendszerbõl lehet meghatározni.
Az eredmény két hullám megoldás, melyek sebességének abszolútértéke
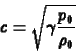 |
(36) |
Az entrópiahullám lényegében a konvekciós egyenletben megismert
sûrûséghullámmal egyezik meg. Ha a nyomás és a sebesség konstans,
akkor a sûrûség perturbáció ![]() sebességgel terjed. Az
entrópiahullám onnan kapta a nevét, hogy az
sebességgel terjed. Az
entrópiahullám onnan kapta a nevét, hogy az
Explicit módszerekre és hiperbolikus egyenletekre érvényes a
Courant-Friedrich-Levy (CFL) stabilitási feltétel,
mely azt mondja ki, hogy egy adott rácspontból a fizikai információ
egy idõlépés alatt nem terjedhet távolabbra, mint a diszkrét módszer
által figyelembe vett rácspontok által meghatározott tartomány.
Ezt az általános stabilitási kritériumot a konvekciós egyenletre
és az upwind módszerre vonatkozóan a (12)
egyenletben definiált Courant szám és a
(13) stabilitási kritérium formájában már
levezettük. Az Euler egyenletek esetében a ![]() sebességû
hanghullám terjed a leggyorsabban, így a CFL feltétel a
sebességû
hanghullám terjed a leggyorsabban, így a CFL feltétel a
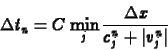 |
(39) |
Az alábbi feladatban véges amplitúdójú hanghullámok terjedését
fogjuk modellezni. A kezdeti feltétel legyen egy
Ellentétben a konvekciós egyenlettel, itt nem tudjuk az egzakt analitikus
megoldást, azonban néhány fizikai megfontolás nagy mértékben
megkönnyíti a numerikus eredmények kiértékelését. A nyomás
perturbáció két balra és jobbra haladó hanghullámot kelt. Ezek
közelítõleg
![]() sebességgel fognak terjedni.
Mivel a hullámok amplitúdója nem elhanyagolhatóan kicsi, nem lineáris
jelenségek fellépésére is számítani kell, azaz a hullám profilja
fokozatosan eltorzul.
A kezdeti feltétel izotermikus, azonban entrópiája nem konstans, tehát
egy entrópia hullámra is számíthatunk, ami
sebességgel fognak terjedni.
Mivel a hullámok amplitúdója nem elhanyagolhatóan kicsi, nem lineáris
jelenségek fellépésére is számítani kell, azaz a hullám profilja
fokozatosan eltorzul.
A kezdeti feltétel izotermikus, azonban entrópiája nem konstans, tehát
egy entrópia hullámra is számíthatunk, ami ![]() miatt helyben fog
maradni.
miatt helyben fog
maradni.