


Next: Feladat: upwind módszer kontinuitási
Up: Gáz és plazma dinamika
Previous: Feladat: FTCS módszer a
Tartalomjegyzék
Stabilitás
Az elõzõ fejezetben felírt (6) diszkretizált egyenlet
nem mûködik megfelelõen mint az a 2. feladat megoldásából
kiderült. Ennek az az oka, hogy a kontinuitási egyenletre az FTCS
módszer numerikusan instabil. Ezt könnyen láthatjuk, ha
elvégezzük a Neumann féle stabilitási vizsgálatot. Bontsuk fel
a kezdeti feltételt Fourier komponensekre, és vizsgáljuk meg,
hogy az egyes komponensek amplitúdója hogyan változik az FTCS
módszer alkalmazása során. Mivel a (6) egyenlet lineáris
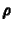 -ban, valamint a határfeltételeket periodikusnak választottuk,
a stabilitás analízis egzakt eredményt fog adni. A
-ban, valamint a határfeltételeket periodikusnak választottuk,
a stabilitás analízis egzakt eredményt fog adni. A 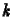 hullámszámú
Fourier komponens a
hullámszámú
Fourier komponens a
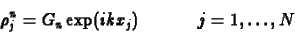 |
(8) |
alakban írható fel, ahol 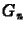 az amplitúdó, és
az amplitúdó, és 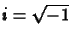 az
imaginárius egység.
Ha behelyettesítjük a (8) formulát az (6)
egyenletbe, akkor a
az
imaginárius egység.
Ha behelyettesítjük a (8) formulát az (6)
egyenletbe, akkor a 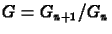 amplitúdó növekedési
faktorra a következõ megoldást kapjuk:
amplitúdó növekedési
faktorra a következõ megoldást kapjuk:
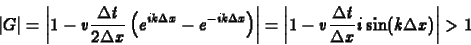 |
(9) |
Mint látható tetszõlegesen kis 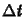 idõlépés mellett is
idõlépés mellett is
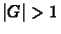 , azaz a Fourier komponens amplitúdója minden lépésben nõ.
Tehát az FTCS módszer a kontinuitási egyenletre nézve instabil.
, azaz a Fourier komponens amplitúdója minden lépésben nõ.
Tehát az FTCS módszer a kontinuitási egyenletre nézve instabil.
Vizsgáljuk meg, hogyan javítható a diszkretizált egyenlet viselkedése.
Az egyik megoldás az, ha a térbeli deriváltat féloldalasra változtatjuk:
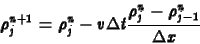 |
(10) |
Természetesen nem mindegy, hogy a bal vagy a jobb oldali differenciát
használjuk. Mivel itt 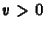 , azaz az áramlás balról jobbra halad,
logikus, hogy a bal oldali
, azaz az áramlás balról jobbra halad,
logikus, hogy a bal oldali
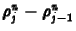 differenciát
használjuk. Ezt áramlásfelöli (angolul ,,upwind'') deriváltnak
nevezzük.
differenciát
használjuk. Ezt áramlásfelöli (angolul ,,upwind'') deriváltnak
nevezzük.
Végezzük el a stabilitás vizsgálatot a (10)
módszerre vonatkozóan.
A (8) Fourier komponsnek az upwind módszer (10)
képletébe való helyettesítésével az erõsítési faktorra a
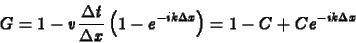 |
(11) |
megoldást kapjuk, ahol
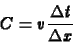 |
(12) |
a Courant szám, ami azt adja meg, hogy 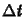 idõ
alatt az információ hány rácstávolságnyira terjed.
A (11) egyenlet szerint az erõsítési faktor a komplex
számsíkon egy
idõ
alatt az információ hány rácstávolságnyira terjed.
A (11) egyenlet szerint az erõsítési faktor a komplex
számsíkon egy 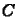 sugarú körön helyezkedik el, melynek középpontja a
valós tengelyen
sugarú körön helyezkedik el, melynek középpontja a
valós tengelyen 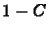 -nél van amint ez a 2. ábrán
látható.
-nél van amint ez a 2. ábrán
látható.
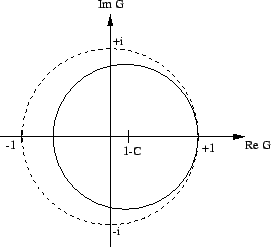
Ábra 2.:
A G komplex erõsítési faktor az upwind módszerre.
G a folytonos vonallal rajzolt körön helyezkedik el.
A stabil tartományt a szaggatott kör jelöli.
 |
A stabilitás feltétele
 |
(13) |
azaz a Courant szám nem lehet 1-nél nagyobb. A 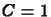 , azaz
, azaz
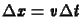 választás rendkívül érdekes eredményt ad,
ugyanis ekkor
választás rendkívül érdekes eredményt ad,
ugyanis ekkor 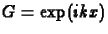 , azaz a Fourier komponens értéke
, azaz a Fourier komponens értéke
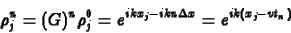 |
(14) |
ami éppen az egzakt megoldása a kontinuitási egyenletnek.
Mivel minden Fourier komponensre egzakt a diszkrét megoldás,
általában is igaz, hogy az upwind módszer a konstans sebességû
kontinuitási egyenletre 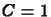 Courant szám mellett egzakt megoldást ad.
Ez másképpen is belátható:
Courant szám mellett egzakt megoldást ad.
Ez másképpen is belátható: 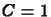 esetén az upwind módszer
minden idõlépésben éppen egy rácstávolságnyival viszi arrébb
a megoldást.
Valójában persze ez nem túl hasznos, hiszen a konstans sebességû
kontinuitási egyenlet megoldásához nincs szükség számítógépes
modellre. Reális, általánosabb egyenletre is jellemzõ eredményt a
esetén az upwind módszer
minden idõlépésben éppen egy rácstávolságnyival viszi arrébb
a megoldást.
Valójában persze ez nem túl hasznos, hiszen a konstans sebességû
kontinuitási egyenlet megoldásához nincs szükség számítógépes
modellre. Reális, általánosabb egyenletre is jellemzõ eredményt a
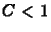 Courant számmal végzett szimulációk mutatnak.
Courant számmal végzett szimulációk mutatnak.
Az is látható,
hogy ha 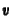 elõjele negatív lenne, akkor
elõjele negatív lenne, akkor 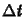 -tõl
függetlenül instabillá válik a módszer. Éppen ezért az
általános upwind módszer
-tõl
függetlenül instabillá válik a módszer. Éppen ezért az
általános upwind módszer 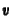 elõjelének függvényében
választja a bal vagy jobboldali differencia formulát:
elõjelének függvényében
választja a bal vagy jobboldali differencia formulát:
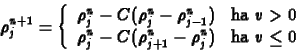 |
(15) |
Az így definiált upwind módszer feltételesen stabil
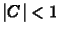 -re, most már
-re, most már 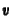 elõjelétõl függetlenül.
elõjelétõl függetlenül.
Alfejezetek



Next: Feladat: upwind módszer kontinuitási
Up: Gáz és plazma dinamika
Previous: Feladat: FTCS módszer a
Tartalomjegyzék
Gabor Toth
2000-09-04
![]() -ban, valamint a határfeltételeket periodikusnak választottuk,
a stabilitás analízis egzakt eredményt fog adni. A
-ban, valamint a határfeltételeket periodikusnak választottuk,
a stabilitás analízis egzakt eredményt fog adni. A ![]() hullámszámú
Fourier komponens a
hullámszámú
Fourier komponens a

![]() elõjele negatív lenne, akkor
elõjele negatív lenne, akkor ![]() -tõl
függetlenül instabillá válik a módszer. Éppen ezért az
általános upwind módszer
-tõl
függetlenül instabillá válik a módszer. Éppen ezért az
általános upwind módszer ![]() elõjelének függvényében
választja a bal vagy jobboldali differencia formulát:
elõjelének függvényében
választja a bal vagy jobboldali differencia formulát: