


Next: Feladat: implicit idõintegrálás kontinuitási
Up: Gáz és plazma dinamika
Previous: Feladat: upwind módszer kontinuitási
Tartalomjegyzék
Explicit és implicit módszerek
Az eddig tárgyalt módszereknél az 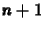 -dik lépéshez tartozó
megoldás egyszerûen felírható az
-dik lépéshez tartozó
megoldás egyszerûen felírható az 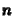 -dik lépésbõl, amint
azt a (6) és (15) algoritmusok is mutatják.
Az ilyen módszereket explicit-nek nevezzük.
-dik lépésbõl, amint
azt a (6) és (15) algoritmusok is mutatják.
Az ilyen módszereket explicit-nek nevezzük.
Diszkretizáljuk a kontinuitási egyenletet
hasonlóan (5)-hez, de most
a térbeli deriváltat az 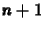 -dik lépésbõl számítsuk ki!
A kapott
-dik lépésbõl számítsuk ki!
A kapott
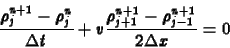 |
(16) |
diszkretizációt implicitnek nevezzük, ugyanis
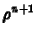 már csak impliciten, egy egyenletrendszer
megoldásaként adott. Jelen esetben egy lineáris
egyenletrendszert kaptunk a
már csak impliciten, egy egyenletrendszer
megoldásaként adott. Jelen esetben egy lineáris
egyenletrendszert kaptunk a
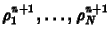 ismeretlenekre.
Ezt az egyenletrendszert már nem olyan egyszerû megoldani,
mint ahogy azt a (6) FTCS módszernél tettük.
Egy dimenziós rácson az egyenletrendszer hatékonyan
megoldható a Gauss elimináción alapuló Thomas algoritmussal.
ismeretlenekre.
Ezt az egyenletrendszert már nem olyan egyszerû megoldani,
mint ahogy azt a (6) FTCS módszernél tettük.
Egy dimenziós rácson az egyenletrendszer hatékonyan
megoldható a Gauss elimináción alapuló Thomas algoritmussal.
Ha elvégezzük a stabilitásvizsgálatot az implicit módszerre,
akkor az erõsítési faktorra a
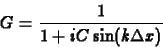 |
(17) |
megoldást kapjuk. Könnyen látható, hogy 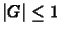 tetszõleges
tetszõleges 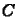 -re, azaz
-re, azaz 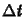 -re. Az implicit módszer tehát
feltétel nélkül stabil.
-re. Az implicit módszer tehát
feltétel nélkül stabil.
Alfejezetek



Next: Feladat: implicit idõintegrálás kontinuitási
Up: Gáz és plazma dinamika
Previous: Feladat: upwind módszer kontinuitási
Tartalomjegyzék
Gabor Toth
2000-09-04
![]() -dik lépéshez tartozó
megoldás egyszerûen felírható az
-dik lépéshez tartozó
megoldás egyszerûen felírható az ![]() -dik lépésbõl, amint
azt a (6) és (15) algoritmusok is mutatják.
Az ilyen módszereket explicit-nek nevezzük.
-dik lépésbõl, amint
azt a (6) és (15) algoritmusok is mutatják.
Az ilyen módszereket explicit-nek nevezzük.
![]() -dik lépésbõl számítsuk ki!
A kapott
-dik lépésbõl számítsuk ki!
A kapott