 LaripS.com, © Bradley Lehman, 2005-22, all rights reserved. All musical/historical analysis here on the LaripS.com web site is the personal opinion of the author, as a researcher of historical temperaments and a performer of Bach's music. "The 'Bach temperament' and the clavichord"© Bradley Lehman, September 2005;
This article is an elaboration and exploration of some of the principles presented in "Bach's extraordinary temperament: our Rosetta Stone"[1]. As I proposed in that article, the musical evidence of Bach's keyboard and ensemble music (both instrumental and vocal), along with the design he drew at the top of the title page of Das wohltemperirte Clavier (1722)[2], converges to a specific temperament on his keyboards. I believe he had this consistent temperament preference or expectation through all or most of his career: a performance and compositional resource he used on his harpsichords, clavichords, and at least some of the organs. Likewise, this temperament solves problems in the music of his sons by presenting a clear and beautiful texture. The temperament's main formulation for solo and instrumental-ensemble music[3] is as follows, based on the Pythagorean comma:
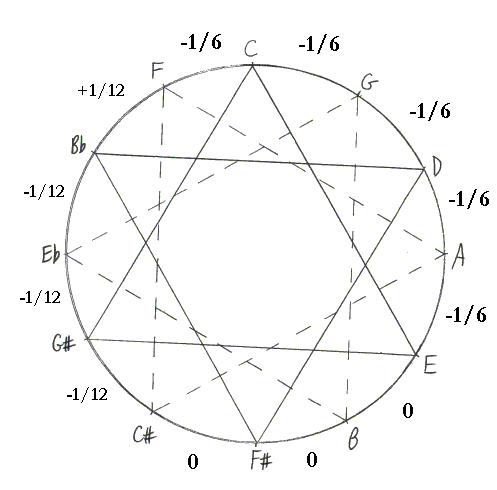
Figure 1: Circle of 5ths in Bach's temperament, with D# and A# renamed to their more familiar functions as Eb and Bb. For a more familiar layout of this as a "circle of 5ths"[4], see Figure 1. Bach's drawing is seen in Figure 2, with the appropriate note-name assignments[5] added in Figure 3. 
Figure 2: Bach's shorthand drawing for his tuning method. This is drawn upside-down at the top of his 1722 autograph title page of Das wohltemperirte Clavier. (For a complete explanation, see "Bach's extraordinary temperament" and http://www.larips.com .)  Figure 3: Assignment of the note names to set up the
temperament. The amount of tempering is
indicated by the various types of loops between these. This temperament gives an exciting, colorful sound and has the flexibility to play equally well in all keys, with no dead-ends anywhere. "Equally well" is not "the same", however. All those major and minor keys sound objectively different from one another, having slightly different semitone and tone arrangements in their scales, and different harmonic balances of the triads and more complex chords. These differences render all the keys recognizably distinct, as to the tensions and resolutions in the way tonal music behaves. The triads and diatonic scales of F and C majors are the closest to regular 1/6 comma.[6] D major and E-flat major each have an average quality resembling equal temperament. The scale of E major is the closest to Pythagorean tuning. We have the complete flexibility of modulation as if it were equal temperament, but also a third dimension of depth: natural motion forward through the music, in a well-organized and dramatic manner. I believe this is what Carl Philipp Emanuel Bach meant when he wrote that "In practice, a keyboard so tuned[7] is the purest of all instruments, for others may be more purely tuned but they cannot be purely played. The keyboard plays equally in tune in all twenty-four tonalities and, mark well, with full chords, notwithstanding that these, because of their ratios, reveal a very slight impurity."[8] Short of hearing this hands-on, directly for oneself at a keyboard instrument,[9] how may we describe the most noticeable musical effects of the temperament? Sharps are high and bright, with a strong and rather "hard" (dur-) tone that creates forward motion when they are used in dominant triads. Flats seem warm and vibrant, soft (moll-) and gentle, with a shimmer to their chords and scales. The naturals, with the exception of B,[10] have the same neutral and resonant character that they do in a complete 1/6 comma layout. The biggest difference here, as compared with other familiar "well temperaments",[11] is the treatment of the flats. With the sharps placed so uncommonly high, the major and minor 3rds are especially euphonious when those same levers are played on the keyboard as flats. They serve very well as the tonic under natural notes, making major 3rds (for example, Db under F, or Ab under C). I have especially enjoyed the (re)acquaintance with music of the Bach family having the notes Ab, Db, Gb, and Cb: hearing the expressive but never jarring effects those notes create in musical contexts. The axis of most symmetry in this temperament is the note C#/Db. It is exactly midway between A and F, creating two equally-sized major 3rds A-C# and Db-F. It is also an exact mean (average) semitone between C and D; and bisects an octave between G on either side. The note G#/Ab is placed quite high, and the interval E-G# is noticeably wider than its counterpart Ab-C. Although this is uncommon next to other temperaments,[12] there is a simple musical logic to it: the note Ab is only four positions away from C by the spiral of 5ths (Ab-Eb-Bb-F-C), while G# is eight positions in the other direction (C-G-D-A-E-B-F#-C#-G#). It makes sense to have Ab relatively better in tune, as to having less deviation from purity as a major 3rd.[13] Because the sharps are so high in most of their musical contexts, they work strongly as leading tones tending to resolve upward--and pressing the music forward, with tension. The flats and naturals create more static effects of calmness and repose. Several of the dominant/tonic relationships in minor keys are especially notable. The two simplest minor keys, A minor and D minor, have the two most unstable dominant triads (because of the exceptionally high sharps, E-G# and A-C#). This relationship is reversed in F minor and Bb minor, the most unsettled-sounding or dark minors, having the most euphonious dominants of C and F majors (thanks to the regularity of 1/6 comma naturals). The scales of E minor and B minor are exceptionally crisp and bright, due both to the pure 5ths on the tonics and the harder-than-average dominants. All of these qualities--and more--are of course better experienced directly at a keyboard, than by attempted description in print. When we view the temperament melodically: the semitones range from 94 to 110 cents, and the tones from 196 to 204.[14] This gives a pleasing and expressive variety to each, while remaining subtle enough that the differences still seem naturally vocal, and do not draw undue attention themselves as any bumpiness.[15] Turning more specifically now to the clavichord, how does all this matter? As a clavichord's notes die away more quickly, compared with the harpsichord or organ, its tuning in general is more difficult to hear accurately. With leeway for Bebung and other expressive pitch-bending with the fingers, and because of the soft volume overall, the clavichord is more forgiving of having almost-correct intervals (while it is scarcely forgiving of anything else!). Still, if at least for the player's sanity and pleasure, the basic layout for equal finger pressure needs to be something reasonable and dependable for the music to be played. Several factors in this are: (1) flexibility to play all the music we care to play (as appropriate to the style and compass of the instrument); (2) euphonious results, at least avoiding grossly noticeable errors of intonation; (3) ease of tuning; (4) the need not to retune too often--which becomes especially bothersome on clavichords that are double-strung, and potentally destructive to the instrument if it is double- or triple-fretted. On fretted clavichords a temperament cannot be reorganized at all without moving some of the tangents to strike different points on the strings: not a recommendable daily practice! To try this experimentally myself, I used my double-fretted clavichord,[16] a Hubert-model Carl Fudge kit built by Brian Joyce in 1984. I converted it from a generic "well-temperament" in about an hour one afternoon in 2004, without any calculations or advanced tools. To do so, I simply tuned all the naturals especially carefully first, in regular 1/6 comma and with the B slightly raised as pure from E. Then, I taped the jaws of two needlenose pliers so the teeth would not make any marks on my tangents.[17] With these pliers I bent the tangents sideways, gently by trial and error, until they now strike the correct-sounding positions.
Having performed this surgery on the sharps' tangents to achieve that result, I have never felt the need to change the instrument again. I merely correct my weather-drifted 1/6 comma naturals occasionally, testing especially with the F# and Bb/A# to make sure my F and B are also correct. This layout allows me to play all the 18th-century music that I care about. 16th- and 17th-century music also sounds pleasant--with enough balance of plain regularity and interesting spice, staying fairly close in character to old-fashioned meantone in the simple keys. Not to neglect 19th- to 21st- century music, either; everything works beautifully in all tonal situations, and any atonal music inherits an interesting variety as well. Richard Loucks[18] has written a thorough study of Bach's WTC as playable on the clavichords that would have been available to him. Loucks examined the various types of "fretting hazards" in dispositions where two notes are shared by a single string.[19] He did not treat issues of possible temperaments, but focused on the way the tangents are able to excite the string (or not) in the physically crunching situations. For unfretted clavichords there is somewhat more flexibility to change temperaments during or between playing sessions, simply by retuning the individual strings. But, how feasible is this beyond being a bother? Perhaps spurred especially by Murray Barbour's articles[20] and book[21], there has been a fashionable notion that a harpsichord or clavichord should be retuned between pieces of the WTC to use different sets of 12 notes, and using basically meantone-derived scales. But let us look more closely at the extant music. The C# minor fugue of book 1 negates this notion of retuning: it uses 14 different notes, G, D, A, E, B, F#, C#, G#, D#, A#, E#, B#, Fx, and Cx. The G, D, Fx, and Cx (among others) occur in accented thematic positions in this piece. This extraordinary fugue has real entrances of its subject in six different keys, and it gives us all of the following diminished 4ths in melodic contexts: B#-E, Fx-B, E#-A, Cx-F#, D#-G, A#-D. Likewise, the G# minor fugue of book 2 uses 14 notes: from A, E, B...to Gx, Dx. From bar 32 to the cadence in bar 35, Bach swapped A to Gx and E to Dx, at close range. In the G minor "English" suite's Sarabande (BWV 808), there is a swap of Db to C# in bars 17-18; and from bars 10 to 21 the B natural changes to a Cb, and back. In Bach's inventions and sinfonias (BWV 772-801) similar problems arise. That book as a whole uses 24 notes in its various compositions. Several of the individual pieces go beyond 12 notes, themselves. The E major invention has 13 notes from D to Cx, and the A minor invention a different 13 from G# to Ab. The D minor sinfonia uses 13 from D# to Eb. The E minor sinfonia has 14 notes from Eb-Bb up to D#-A#. The F minor sinfonia has 15, from Bbb-Fb up to A-E-B. In a later and yet more sophisticated "invention", Bach's first Duetto (BWV 802) goes from Db to E#: 17 notes![22] It makes a virtue of shifting enharmonics within its main theme, presenting the closest possible juxtapositions of A#-Bb, E#-F, C#-Db, and G#-Ab as the piece goes along. Goldberg variation #25 (BWV 988) gives us 17 notes from Fb to G#, and other variations contribute D# and A#, for a total of 19.[23] Contrapunctus 3 of Die Kunst der Fuge (BWV 1080) likewise plays games of close mutation with Eb/D#, Ab/G#, and Db/C#. Whatever instrument(s) these compositions are played on, any proposed retuning before or during the music is out of the question. And, the modulation canon of Das musikalisches Opfer (readily playable as either a keyboard solo or duet, among other options) has an incalculable number of notes as it continues to rise infinitely through enharmonic swaps. To play it merely six times is to use all twelve minor scales in turn, by a spiral-of-5ths progression. Each time we traverse 12 notes in any 12-note temperament--modulating upward or downward along the spiral of 5ths -- we have a Pythagorean comma to gain or lose, whether gracefully or clunkily.[24] We could retune all day, and any compositions that exceed 12 notes (i.e. using some enharmonic equivalences) would still have some wrong notes by the distance of this comma. The simpler solution, instead of retuning, is to have a temperament that gains or loses this comma gradually as we proceed along the spiral of 5ths, so it never makes an obtrusive effect. And that is precisely what the Bach temperament delivers: a smooth way to use the enharmonic shifts so they seem natural. The graph in Figure 4 shows the note-names that normally
occur in music, and demonstrates how the diatonic scales are constructed.[25] Within
this structural model, irrespective of temperament for the moment: any major
scale (or "Aeolian" natural minor scale) is formed by choosing seven
consecutive notes from this, and then arranging them in step order. For example, the C major scale is
F-C-G-D-A-E-B rearranged as C-D-E-F-G-A-B(-C). By contrast, the G major scale
omits F from the left and adds F# at the right, rearranged to
G-A-B-C-D-E-F#(-G). Normal modulation
in tonal music is a process of changing scales, by lopping notes off one side
of the collection and adding them onto the other side. The introduction of a
note foreign to the present scale signals the ear that we are switching to a
different scale containing it.[26] For example, in bar 6 of Bach's C major
prelude, WTC 1, the intruding F# (foreign to the C major scale) tells
the listener that the music is moving into G major. The diagonal on this graph shows
equal temperament: all its notes are exactly the same distance apart,
geometrically. Therefore, all the major or minor scales in equal temperament
have the same "shape" or character as one another, a steady slope.
Modulation does not accomplish very much, because each new scale we go to
sounds the same.[27] Equal
temperament emphasizes melodic smoothness, with a bland equality of chromatic
and diatonic semitones: it becomes hardly relevant--other than a pedantic
point--to spell the note names correctly. In a closer look at the 1/6 comma
levels: the horizontal lines on this graph show the 18th century
orchestral standard of 1/6 comma tuning. The notes in the middle section
(level 0) are all in tune with one another, level on the same layer,
emphasizing harmonic smoothness. The
notes to the left of E-flat are all one comma too flat (i.e. --100%), and the
notes to the right of G-sharp are all one comma too sharp (+100%). That is, reiterating a point mentioned
above: each time we travel twelve notes in either direction for an enharmonic
note-name, we must add one Pythagorean comma to get to the next layer. Notes such as Eb and D# really are different
from one another. 18th century
musicians were trained to sing and play them with an understanding of that
difference, inflecting chromatic semitones smaller melodically than diatonic
semitones. Intervals that include notes
across the gaps have a "wolf" quality to them, due to the misspelling
of the intonation. There are eleven
similar fifths and one wolf diminished sixth; eight similar major thirds and
four wolf diminished fourths.[28] Bach's temperament, the plotted
zigzag here, bridges those rough gaps by making the notes gradually blended
from one layer to the next. The numerals below each column here indicate the
percentage of the Pythagorean comma in deviation from the regularity of
extended 1/6 comma temperament. B and the sharps are at tastefully compromised
positions, tuned rather high so they can serve also as flats; and each of these
is differently compromised, giving each note a subtle "personality"
distinct from regularity. Every scale sounds different from
every other, because each subset of seven consecutive notes has a different
shape in the relationships of those notes. To see this: make a template with a scrap of paper, or use your fingers,
to view only seven notes of this graph at a time. Then move it left or right,
and notice how the shape of the plotted Bach curve across seven notes is
different for each of the twelve starting points. The interrelationships of these notes, being tastefully out of
tune by various percentages of a comma, form distinctive major and minor scales
on all degrees.[29] C major is the most like regular 1/6 comma
tuning, with a simple and gentle sound, because six of its seven notes are in
those normal horizontal positions. A-flat major (notes Db to G) is the most like equal temperament, as the
slope is most similar to that diagonal. E major (A to D#) resembles the steeper slope of Pythagorean tuning. The explanation here--and the close analysis of scale structure and the music--has been rather theoretical, and perhaps daunting. However, it is all derived from and inspired by nearly 18 months of regularly playing and listening to this temperament, especially in the music of JS Bach and his sons. I practice this music on my clavichord, harpsichords, in visits to an organ in Indiana[30], and on several pianos.[31] This temperament reveals marvelous colors in all of this repertoire, along with dramatic and beautiful contrasts that are never harsh. I am especially fond of the expressive effects within the slow movements of CPE Bach's sonatas, where he so frequently mixed melodic notes or ornamentation into foreign harmonies, creating exquisite tensions and resolutions. To hear how much difference this temperament makes, the reader is invited to explore similar or additional experiments along this line of playing the music; and to test the same repertoire in the competing temperaments of Vallotti, Werckmeister III, Neidhardt's temperaments of the 1720s, et al.[32] A number of players, both expert and amateur, have expressed their initial surprise that Bach's A major and D major are less relaxed in character than other contemporary temperaments had led us to expect. Remember, however, that Bach's expressly pedagogical compositions all emphasize a melodic manner of playing and listening, through independent contrapuntal lines--not much harmonic basking in long-held consonant chords. This temperament helps us to understand such a musical approach more directly, where harmony arises from the confluence of linear motion, singable melodies: as can also be experienced playing through Bach's collected four-part chorales.[33] Tuning instructionsFor practical instructions to set this Bach temperament on a clavichord or harpsichord, I have provided several methods at the web site http://www.larips.com . The simplest is as follows, referring again to Bach's drawing in Figure 2, and its mapping with note-names in Figure 3:
Endnotes[1] Bradley Lehman, "Bach's extraordinary temperament: our Rosetta Stone" Early Music 33:1 (February 2005) pp3-23, and 33:2 (May 2005) pp211-231, plus the 66 additional pages in five supplemental files available through Oxford University Press's web site. An outline linking all these portions is available at http://www.larips.com , including additional clarifications of the article. [2] Bach's autograph score dated 1722, now in the collection of the Staatsbibliothek zu Berlin Preußischer Kulturbesitz. [3] There is also an important transposed reading of the temperament for most of Bach's vocal music in rehearsal and performance, starting with G-D-A-E-B-F# tempered 5ths. However, this does not concern the quiet clavichord. [4] The circle of 5ths is illustrated as Johann David Heinichen's "Musicalischer Circul" in Der General-Bass in der Composition, 1728. [5] Other theoretical readings from this Bach drawing exist, assigning meaning to it from different sets of premises, and resulting in different layouts. Andreas Sparschuh's abstract from a 1999 mathematical lecture is now available on his own web site (posted mid-June 2005 and sent to me in e-mail at that time). Michael Zapf's informal materials from 2001-5 are available in his Internet discussion group "Yahoo! Clavichord". More recently, several others have proposed additional readings from the drawing, either in letters to Early Music or in Internet postings and discussions. In response to these premises (Bach as a theoretical mathematician; integer beats per second at specific frequencies; presumed practical "difficulty" of 1/6 comma regularity; starting points; assumptions about the 12th "5th"), I have collected and analyzed these other resultant readings and methodologies in a feature page at http://www.larips.com . The obvious tests for each are: study the extant historical record about practices and aesthetics in Bach's milieu, and about Bach's personal character and teaching methods; and play the full range of Bach's repertoire to hear if these temperaments make plausible sounds. [6] The use of the word "regular" here indicates that all of the correctly-spelled 5ths are the same size as one another. Every 12-note keyboard temperament has eleven 5ths plus one leftover diminished 6th (such as G#-Eb, or A#-F), which might or might not be the same size as the 5ths. [7] He described a general manner of tempering "most of" the 5ths (meisten Quinten), without divulging which ones or by how much. [8] Versuch über die wahre Art das Clavier zu spielen, Berlin, 1753; from paragraph 14 of the Einleitung. Translated by William J Mitchell as Essay on the True Art of Playing Keyboard Instruments. New York: Norton, 1949. This point is explored more fully at my web page http://www.larips.com . [9]
Organ and harpsichord recordings by the author
are available from http://www.larips.com ,
in a co-production with Goshen College (Indiana, USA). This temperament is built into Goshen
College's organ (Taylor & Boody Opus 41, 2005) and the organ at the Laajasalo Church in Helsinki, Finland
(Orgelbau Kögler GmbH, 2005). The
forthcoming Harmonia Mundi recording of Bach's "Goldberg Variations", played by
Richard Egarr, also uses this temperament. [10] B is slightly raised, bridging the character toward the increasingly sharpened sharps F#-C#-G#...; and giving a bit of hardness or fortitude to the G major triad and scale. [11] "Vallotti", "Werckmeister III", "Barnes-Bach", "Kellner-Bach", Neidhardt and Kirnberger systems, et al. [12] Most other temperaments of the period have E-G# noticeably smaller than Ab-C, with Ab-C being as wide as Pythagorean, or even worse (in the layouts sticking more closely to the classic Eb to G# disposition of meantone). A notable exception is Neidhardt's 1724 organ temperament for a "Dorf" (village) which has G#/Ab exactly halfway between E below and C above. Another is Sorge's 1758 temperament for Chorton organs, having the rare feature of a wider E-G# than Ab-C. My hypothesis is that Sorge learned this from Bach, his colleague in the Mizler society: either during Bach's last decade or by studying the Leipzig organs himself after Bach's death. [13] Ab-C is 73% of a syntonic comma sharp from a pure major 3rd; contrast the 91% of E-G#. These high-seeming numbers are the price to pay for having C-E at only 27% sharp. Equal temperament, for comparison, has all major 3rds at 64% of a syntonic comma sharp: all at a consistent average point. [14] The averages in any twelve-note temperament are the 100 cent semitone and 200 cent tone, found throughout equal temperament and defined by it. [15] Any notions of quality are obviously subjective, and a function of musical taste, although the ranges are objectively measureable. Readers are invited to draw their own conclusions about melodic and harmonic features by playing a wide variety of music, especially compositions by the Bachs. [16] I did not have to change any of my bass tangents, as this clavichord is unfretted below the tenor register. The required surgery was only on the upper two-thirds of the instrument. [17] Consult with instrument builders and other players first, if worried about bending or adjusting a favorite instrument! My point here is simply that a practical and musical conversion need not involve any mathematical calculations, or any enormous amount of time and effort. [18] Richard Loucks, "Was the 'Well-Tempered Clavier' performable on a fretted clavichord?" in Performance practice review 5/1 (1992), pp44-89. [19] To experience this directly on a double-fretted instrument with D and A free (i.e. not sharing any semitones on these two strings), try for example the right-hand parts of book 2's E major prelude or F minor fugue, or the B major prelude of book 1. Loucks also treats the less common fretting layout that has A and E free. [20] J Murray Barbour, "Bach and The Art of Temperament", in Musical Quarterly 33:1 (1947) pp64-89; Barbour, "Irregular systems of temperament" in Journal of the American Musicological Society 1:3 (1948) pp20-26; and Barbour, "Temperatur und Stimmung", in Die Musik in Geschichte und Gegenwart Band 12, Friedrich Blume (ed.), Kassel, 1965, pp. 213-227. [21] J Murray Barbour, Tuning and Temperament: A Historical Survey, 1951 and reprinted 2004 with corrected page-numbers in its index. It is based upon Barbour's 1932 dissertation, from Cornell University. [22] Published by Bach in Clavierübung III, 1739; the other three Duetti here also each exceed 12 notes. [23] Even if we were to play this piece on a harpsichord having split accidental keys, with correct spellings to some regular temperament, we are still lacking Cb and Fb and they create wolf moments. [24] See pp214-218 of "Bach's extraordinary temperament", part 2, for more thorough discussion of this. [25] This theory of scale structure is developed and presented thoroughly by Easley Blackwood Jr in The Structure of Recognizable Diatonic Tunings, Princeton 1985. [26] This is rather like "mutation" in the old hexachord system, where the set of "Ut Re Mi Fa Sol La" shifts to various starting positions. [27] The distinction we are drawing here is about intervallic relationships within scales; not overall pitch level. [28] This is true of any regular system, i.e. a temperament having all the correctly-spelled 5ths the same size as one another. [29] To experience this directly in the sound: set up the Bach temperament on a harpsichord or clavichord, and then play all the major scales in turn (C, G, D, etc), listening closely to the intonation quality as each successive sharp or flat is added at the 7th degree. The scales gently metamorphose from one into the next. [30] Taylor & Boody Opus 41, 2005, at Goshen College Music Center in Goshen Indiana USA. Details of this instrument are available at http://www.gcmusiccenter.org . [31] The temperament renders tonal piano music colorfully and suavely, too: try especially Mozart, Haydn, Beethoven, Chopin, Grieg, and Brahms. Several correspondents have reported similarly delighted experiences to me, having their own pianos tuned this way. The piano seems more resonant, more relaxing to play in long sessions, and all the music emerges with greater intensity than it does in equal temperament. Other correspondents and acquaintances have used this additionally on fortepianos, beginning with a Swiss Radio broadcast by Robert Hill in May 2004. [32] A broader roster of temperament recipes is available in Oxford's supplementary web files at http://em.oupjournals.org/cgi/content/full/33/1/3/DC1 , and of course elsewhere in the tuning literature. [33] "The 371" collected and edited by CPE Bach, Riemenschneider, et al.
|
v Introduction > Articles - Outline - Errata * Clavichord - ArtOfTemp - TheTuning v FAQ v Practice v Theory v History v Etc v Recordings |
 Figure 4: The
notes in scales are generated by an extended series, as shown here. Two regular systems shown here are
1/6 Pythagorean comma temperament (the horizontal lines), and equal temperament
(the diagonal). The plotted curve shows
the note placements in Bach's temperament, with numbers indicating the
percentage of a Pythagorean comma that each note deviates from regularity.
Figure 4: The
notes in scales are generated by an extended series, as shown here. Two regular systems shown here are
1/6 Pythagorean comma temperament (the horizontal lines), and equal temperament
(the diagonal). The plotted curve shows
the note placements in Bach's temperament, with numbers indicating the
percentage of a Pythagorean comma that each note deviates from regularity.

