Origins of Terms in International Economics
|
Here I record what I have been able to learn about the origins of some of the terms we use in international economics, both who introduced their meanings and who first gave them their names, if those are not the same people. If the answers to both are included in the Glossary entry itself, then I don't bother with it here (e.g., absorption approach)
If I attribute a concept or the term for it to a particular author, that means I have personally checked the source and seen it used there in the way that I describe. However, if I say or imply that this was the first use of a concept or term, I obviously cannot always know that for certain. For most of these, I have searched in Google Scholar to find the first use of the term identified there. Google Scholar allows one to search a range of years, which is helpful, but not always correct, requiring some care. But I don't know how complete that tool is (it seems remarkably good), and in any case I can't find who may have used a term orally with their colleagues or students without publishing it earlier. If you know of prior uses that should be mentioned, please let me know, preferably by e-mail to alandear@umich.edu. More recently -- 2024 and after researching a large number of these -- I have found that I can use regular Google, instead of Google Scholar, to search by date. I don't know how Google identifies dates, however, but this too has been useful on occasion. Finally, since neither of these sources seems to capture the news sources that I subscribe to -- Economist, Financial Times, New York Times, and Wall Street Journal -- I now may search them as well. Unfortunately for my purposes, New York Times is the only one that seems to allow me to search far back in time. The others only cover fairly recent years, which is not very helpful. |
Index of Origins
| Aggressive unilateralism | |
|
The term itself appeared three times prior to 1990, in writings by Carlton and Bixler 1962, Carlton 1963-64, and Etzold 1982, but always in the non-economic context of the Cold War and military conflict. For example, Carlton and Bixler worried that the American right wing would "come to power in the United States and build a garrison state, pursue policies of aggressive unilateralism, ...."
In the context of economics and trade policy, the term was coined by Bhagwati (1990), who also used it that same year as the title of a volume that he edited with Hugh Patrick. | |
| Asian Tigers, Tiger economy | |
|
I've not been able to track down the first use of this term to refer to the foursome of Hong Kong, South Korea, Singapore, and Taiwan. Everywhere I've seen the term used in writing, the author seems to assume that it is already familiar. The earliest source for "Asian Tigers" in Google Scholar is a book first published in 1983, but I've found only the much later 8th edition, and I suspect that the term did not appear in much earlier editions.
Google also finds a mention of tiger economies in a paper on Southeast Asia in the 1985 Philippine Journal of Third World Studies, but I haven't been able to access that journal to see if they are named there. I suspect not. So the earliest explicit use of Asian Tigers to mean these four countries seems to be in 1987, and in that year it appeared twice. Rabushka (1987) had the following: "The four Asian Tigers -- Hong Kong, Singapore, Taiwan, and Korea -- are renown [sic] as the hyper-growth economies of the Pacific Rim." and Griffith (1987) had
| |
| Atlas method | |
|
The Atlas method got its name from its use in the World Bank Atlas, more recent editions of which are called the Atlas of Global Development.
The current method seems to have been used first in the 1985 edition of the Atlas, where it said "...the procedures for estimating gnp in U.S. dollars differ from those used in previous years." Previous editions had used average prices and exchange rates from a three-year base period, whereas the new procedure was to use "the simple average of the exchange rates for the current year and for the two preceding years; the latter two exchange rates are adjusted for differences between domestic and U.S. inflation." The most important difference between the new and old methods was that the old one used a different conversion for a given year in successive editions of the Atlas, making comparisons difficult. I am unable, from reading details of the prior procedure, to tell whether the new one also causes other differences. In any case, it seems that the subsequent use by others of the Atlas method has been to use the method introduced in World Bank (1985). In an effort to determine whether the Atlas method had a prior history, I have used Google Scholar to search for Atlas method over various years. The term itself was used with other meanings prior to its use by the World Bank, as well as subsequently: a method of measuring the maturity of skeletons; a method in meteorology for detecting weather events; a tool for measuring the "HLB value of a reagent," whatever that is, by Atlas Chemical Industries; and an exercise program by body builder Charles Atlas. The earliest mentions of the World Bank's Atlas method were in 1980, where I found two. One of these (by M.Y. Smith, "Romania: forecasting and development," in Futures) mentioned "following the World Bank Atlas method of adjusting official Romanian national accounts data." The second (by Davies, Grawe, and Kavalsky, "Poverty and the Development of Human Resources: Regional Perspectives," World Bank) had a table of GNP per capita data labeled "IBRD Atlas method, US dollars." From these it appears that the term Atlas method predated the version of World Bank (1985) and referred to the method used in prior editions, which seems to have been slightly different. | |
| Balance of trade | |
|
Price (1905) examined the origins of this concept, the exact wording of which appeared in 1615 and the concept of which, without the wording, can be found as early as 1381 in England, when writers were concerned that by importing a greater value than it was exporting, England was losing money -- i.e., gold and silver. Somewhat before the term balance of trade appeared, similar concerns were said in 1601 to be due to "overbalancing of foreign commodities." From the discussion by Price, it appears that balance of trade in this early use referred to a situation in which values of exports and imports were equal, rather than today's use measuring the extent to which they are unequal.
Fetter (1935) dated the term to 1623, apparently disagreeing with Price that its use in 1615 was comparable. His main concerns were with the common attribution that a positive balance of trade is "favorable" and with whether the term includes only trade in goods or instead extends beyond that to include other payments such as we today would include in the balance on current account or even balance of payments. It appears that early writings used the term variously in each of these senses. [I was alerted to the articles by Price and Fetter by Obstfeld (2012).] | |
| Banana republic | |
|
As explained nicely in Economist (2013), the term was coined by the writer O. Henry in a short story in 1904, set in a fictional land he described as a "small, maritime banana republic." He was living at the time in Honduras, on which he must have based his description. Honduras was and remains one of the countries that rely heavily on plantations of bananas, owned by what was then the United Fruit Company, now called Chiquita.
| |
| Beggar thy neighbor | |
|
It has become commonplace, at least in the literature of economics, to describe policies that decrease imports as beggar thy neighbor policies. These policies include most obviously increases in import tariffs and artificial depreciation of currencies. The basis for this label is that these policies can benefit the home country only by hurting its trading partners. Today we most commonly interpret those effects as changes in overall economic welfare, but historically the term was first used during the Great Depression, when the effects were on employment.
The origin of the term was nicely discussed by Weisman (2009), who credited it to Joan Robinson (1937), whom he thanked "for such a vivid phrase." He also pointed out that she likely got the phrase from a 19th century card game, Beggar My Neighbor, of which he said the "first literary appearance ... was in the novel Great Expectations, published in 1861" by Charles Dickens. That is especially plausible given that Robinson herself never used the term beggar thy neighbor, but only >beggar my neighbor. It appears in the title of her essay, "Beggar-my-Neighbour Remedies for Unemployment," and in several passages as the "game of beggar-my-neighbour," such as (p. 156):
The first use of the term that I can find in a context of international trade showed up in an un-authored piece, perhaps an editorial, in the Honolulu, Hawaii, Daily Herald, June 3, 1887. An article titled "The Sugar Industry" discussed how multiple countries were exporting sugar at below their domestic prices and less than the cost of production (what today we would call dumping), "the idea apparently being to ruin the British refiner at the expense of the foreign taxpayer." Before that it says, "It is a singular game to play something like that known as beggar my neighbor." While the context was trade, the objective was clearly not what we would mean by it today. The first clear use of the term with today's trade meaning preceded Robinson (1937) and was by Reynolds (1934, p. 180):
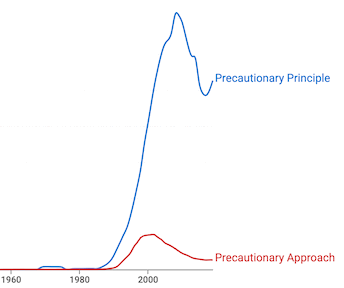
It is therefore not certain that Robinson should have the credit that Weisman gives her for introducing the term beggar my neighbor (not beggar thy neighbor) to the literature on international trade. But to the extent that the term caught on, it does seem likely that Robinson's greater visibility compared to Reynolds and Elliott would have been the cause. And catch on it did. In the decade 1940-49, Google Scholar finds at least 18 articles including beggar my neighbor in the context of international trade, including six in the American Economic Review. The peak was five articles in 1947. But that is not the term that is most widely used today. Instead beggar thy neighbor has largely replaced beggar my neighbor, as we can see from Google's NGram of the two terms:
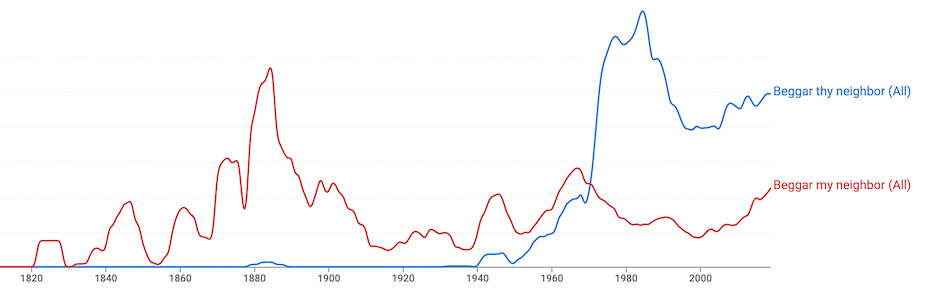
The surge in appearances of beggar my neighbor in the 1800s presumably reflects the popularity of the card game, which then declined. One sees the rise in its use in the 1930s and 1940s, perhaps showing its rise in the context of international trade, which took off even more in the 1950s and 1960s. But beggar thy neighbor appeared for the first time in the 1940s, then took off in the late 1960s, and it has dominated beggar my neighbor ever since. Searching for appearances of beggar thy neighbor in Google Scholar, the first I find is Berge (1946, p. 687) who wrote, in discussing the Great Depression:
It was not until the early 1950s that beggar thy neighbor began to appear in the economics literature, first by Hildebrand and Mace (1950) in Review of Economics and Statistics and then by Kindleberger and Despres (1952) in American Economic Review. The latter included (p. 332)
But why did he or someone else feel the need to change beggar my neighbor into beggar thy neighbor? I can only offer my own speculation, which others may find either obvious or silly: The card game that seems to have started all of this was all about deliberately eliminating the other players in order to win the game. So beggaring one's neighbor was not only the object, but something to be applauded. Thus it was desirable for one to focus approvingly on the negative effects one could have on one's own, i,e. "my," neighbor. But as the game came to be used as a metaphor for destructive competition, the focus shifted to the negative effects that others would have on ourselves, and therefore the perspective moved to that of the neighbors. Beggar thy neighbor therefore speaks disapprovingly from the neighbor's point of view and stresses that negative connotation. As the NGram chart above shows, beggar my neighbor has not entirely disappeared. And while economists generally disapprove of uses of trade and exchange rate policies to benefit oneself at the expense of others, there are undoubtedly some who still -- from a nationalist perspective and discounting the likelihood of retaliation -- favor such actions. It would be interesting to see whether current uses of beggar my neighbor tend to correlate with that point of view. Perhaps those who use beggar my neighbor in the context of international trade continue to see trade as a zero sum game, which the original Beggar My Neighbor game certainly was, while those who recognize that international trade is a positive sum game have shifted to beggar thy neighbor.
| |
| Belt and Road Initiative | |
|
China's President Xi announced the beginnings of what is now called the Belt and Road Initiative in 2013 visits to Kazakhstan and Indonesia. It ultimately was to include two parts. The Silk Road Economic Belt, announced in 2013, would be a network of rail, pipelines, and roads together with improved border crossings through Central Asia, South Asia, and Southeast Asia. The Maritime Silk Road, announced a bit later at a summit of ASEAN, would consist of development of ports in Southeast Asia, the Indian Ocean, East Africa, and even Europe.
Together these two parts were named One Belt, One Road. The purpose was not just to facilitate greater trade between China and other countries, but also to increase China's influence in those countries and even to foster greater use of the Chinese currency. The change to calling it the Belt and Road Initiative in English is explained in this passage from The Economist, June 11, 2022:
| |
| Benign neglect | |
|
This term cropped up only occasionally prior to 1970, and never in reference to policies regarding the balance of payments. Google Scholar finds it less than once a decade during 1800-1899 and less than once a year during 1900-1969, on topics as diverse as public interest law, African newspapers, and spiders. One source credited the term to "Earl of Dunham's prescription in 1839 for the proper British attitude toward Canada."
Then suddenly in 1970, Google Scholar finds 100 occurrences of the term in that year alone, though still never in an international economic context. This explosion of uses of the term followed wide reporting of a memo by Daniel Patrick Moynihan, counselor to President Nixon. Moynihan wrote:
In 1971 there were at least nine uses of the term benign neglect with the meaning used here: that the US either was doing or should have been doing nothing about its balance of payments deficit, leaving policy responses to other countries. Many of the authors who used the term put it in quotation marks, but none of them said whom they were quoting, if anybody. Many were critical of the policy itself, referring to "experts" or "economists" who advocated the policy, but mostly without naming them. The policy of benign neglect, but without that name, was attributed by Halm (1968) to Despres, Kindleberger, and Salant (1966). According to Halm, p. 1:
After discussing this "minority view" extensively, Halm concluded that "The solution suggested by the minority view suffers from several weaknesses, which make it unlikely that it can supplant or even decisively influence the majority view," and he went on to list 12 "points of contention." Later writers more frequently credited the policy, though again not the name, to Krause (1970) who advocated "A Passive Balance-of-Payments Strategy for the United States" in an article with that title in Brookings Papers on Economic Activity. Krause too, however, made no use at all of the words "benign" or "neglect." Instead, it seems to have been Haberler and Willett (1971), also arguing for a "passive balance of payments policy," who then went on describe it as a "policy of benign neglect":
Rather surprisingly, neither Krause nor Haberler and Willet cited either Depres et al. (1966) or Halm (1968), even though the policy they advocated seems the same as that of the former. The Haberler and Willett paper was dated January 1, 1971, only a few months after Krause, and neither of these papers mentioned the other. So it appears that they may have arrived independently at the same policy recommendation both as each other and as Depres et al. As for calling it the policy of benign neglect, that seems to have originated with Haberler and Willet. Halm in his title had mentioned "deficits benign and malignant," but it does not appear that Haberler and Willet took the word "benign" from him, since they do not cite him. Instead, I conclude that Haberler and Willet were the first to apply the already familiar term benign neglect to US balance of payments policy.
| |
| Blood diamonds, Conflict diamonds, | |
|
These two terms are both used to mean "rough diamonds used by rebel movements or their allies to finance armed conflicts aimed at undermining legitimate governments," according to the website of the Kimberly Process, which initiated a mechanism to prevent them being traded. Another source goes on to say "These diamonds are often mined using forced labor, including children, and are traded illegally to fund violent conflicts and human rights abuses."
[Source]
The organization Global Witness was the first to draw attention to this issue in its 1998 report, "A Rough Trade". That report, however, did not use either of these terms, even though it used the word "conflict" numerous times. Brittanica and others seems to give credit to the United Nations for coining the term:
The very specific UN definition of blood diamonds was formulated during the 1990s, when brutal civil wars were being waged in parts of western and central Africa by rebel groups based in diamond-rich areas of their countries. [Source] The earliest I find from the UN was a press release of December 1, 2000. It included "conflict diamonds" 66 times (and "blood diamonds" only once, the latter reporting a contribution by Argentina). As early as 1997, the UN Security Council began adopting resolutions concerning the situation in African countries and the problems of trade in diamonds, notably in Angola. But only in March 2001 did its resolutions begin referring to conflict diamonds, and they never mentioned blood diamonds. It seems, therefore, that while concern about the phenomenon began in the 1990s, use of the terms began only in 2000. To confirm that the terms were not used prior to 2000, I used Google Scholar to search for them in prior years. While that process is not perfect, I was not able to confirm any use of either term in 1999 or before. Searching in the year 2000 alone, however, I found 43 appearances of conflict diamonds, so that term clearly took off. Similarly, I found 23 appearances of blood diamonds in 2000. As is often the case with Google Scholar searches, some of the appearances in both cases were mis-dated, but I was able to confirm that most of them were truly in 2000. With that many, it seems unlikely that they were prompted by the use of the terms by the UN, at least not by that press release from December 2000. It appears, therefore, that whatever role the UN may have played in using these terms, the public picked both of them up in 2000, and I cannot pinpoint who really coined them. One source in October 2000 mentioned "the coining by the media and advocacy groups of the concept of 'blood diamonds' (i.e., diamonds procured in and through intrastate conflicts)". [Source] The term conflict diamonds was pretty clearly used first, but blood diamonds followed quickly and soon surpassed it, as the following NGram chart demonstrates: 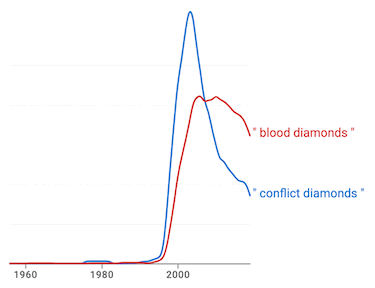 I should note that it was not until a few years later that the term was further popularized in the title of the movie Blood Diamond which appeared in 2006. | |
| Boycott | |
Very nicely explained by Mulder (2022, p. 37):
| |
| Brain drain | |
It seems clear that this term, as meaning the emigration highly trained people, was introduced in a committee report commissioned by the UK Royal Society in 1963. Cervantes and Guellec (2002) say:
My search for use of the term prior to 1963 fails to find any use of the term with this meaning, and the few uses that I do find are in a medical context about drainage from the brain. Then in 1963 I find several uses of the term in the emigration context, some including it in quotation marks suggesting that it was recently introduced. Searches after 1963 find it surging in frequency, as is also indicated by the following Google N-gram graph: 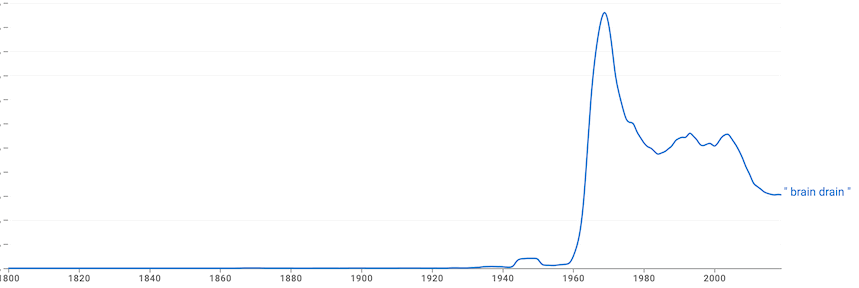
| |
| Canonical model of currency crises | |
|
Krugman (1997a) gave credit for this model, which he seemed in this source to be the first to call the canonical model, to apparently unpublished "work done in the mid-1970s by Stephen Salant, at that time at the Federal Reserve's International Finance Section." Salant focused on schemes to stabilize commodity prices, as described briefly in Salant and Henderson (1978). There it was applied to the market for gold. Krugman then drew on that work for his model of currency crises in Krugman (1979b), and it was refined by Flood and Garber (1984).
| |
| Carousel approach | |
|
Also called carousel retaliation, this was introduced to US legislation in 1999 by a group of senators led by Mike DeWine of Ohio and a group of representatives led by Larry Combest of Texas. The Senate bill was "S. 1619, the Carousel Retaliation Act of 1999." I have not been able to locate that, but it seems to have been the first use of this term. The bill was a response to concern that the retaliatory tariffs used by USTR in the beef hormone case would not be effective, and it was introduced as an amendment to Section 301. The following year, the content of the bill, but not its name, was included in P.L. 106-200, May 18, 2000, the Trade and Development Act of 2000.
Since then, carousel has continued to be used in this context, including as a verb: "to carousel the tariffs." For for more on this history of the carousel approach, see Griffin (2019).
| |
| Carry trade | |
|
This term mystified me when I first learned it, and to some extent it still does. It means borrowing in one currency and lending in another so as to profit from a difference in interest rates. To me as a trade economist, this was not trade, since it does not involve exports or imports. And it was not obvious what is being carried. I now accept that purely financial transactions are often called trade -- trade in financial assets. As for the "carry" part, I first thought that it referred to the "carrying cost" of holding the purchased bond, which is the interest paid on the one sold. But I've since learned that in financial markets more generally, not just international, a difference in interest rates that an actor exploits by both borrowing and lending is called the "carry." Thus if they can lend at a higher rate than they pay to borrow, that is called a "positive carry" while the opposite is a "negative carry". [Source] That may be enough to explain why "carry trade" is used for international actions that I was taught were interest arbitrage, either covered or uncovered. My search for the term "carry trade" did not find it at all with this meaning until 1996, even though such transactions must have been common long before. I learned from Eichengreen and others (e.g., Eichengreen and Mathieson (1998)) that similar actions in 1992 had been called convergence plays. This term, though more awkward, made more sense to me than carry trade since the traders in 1992 were acting on their expectation that interest rates in Europe would converge. This would increase the prices of the high-interest rate bonds and provide capital gains to their holders, in addition to the higher interest rate. For a while, as my searches for "carry trade" found many occurrences of cash and carry trade, I suspected that this was an earlier term for carry trade that had later been shortened. But while my searches found several distinct meanings for "cash and carry trade," none were for what is now called carry trade. One of them, however, concerned actions in bond and futures markets, where again the "carry" was the interest rate differential. My search for the two words "carry" and "trade" together found many uses of them with other meanings, most commonly referring to the carrying of traded goods. The earliest example was Decker (1749, p. 21) which included
I found carry trade with its current meaning first appearing in several news sources in 1996. The trade then was between Japan and the US, exploiting low interest rates in Japan and high in the US. The earliest I found was Wyatt (1996):
Then in 1997, I also found carry trade with its current meaning, now prompted by the role that it played in the Asian Financial Crisis. The earliest was: Fuerbringer (1997):
For years, because of rock-bottom interest rates in Japan and low rates in the United States, banks, investment houses and insurers had borrowed in yen and dollars and put the proceeds into short-term notes in Southeast Asia that were paying far higher rates. These are the so-called carry trades. I also found two other sources in 1997 that used carry trade in this sense, both in the publication Challenge. The first, Roach (1997, p. 104), mentioned two specific uses of carry trade, one in 1993:
A more recent discussion of carry trade was in Frankel (2013), who provided a "'Carry Trade' Model of Commodity Prices" motivated by work on commodity carrying costs by Working (1949) and others. He noted the following:
| |
| CES function | |
|
Arrow et al. (1961, pp. 225-226) described their empirical motivation to "derive a mathematical function having the properties of (i) homogeneity, (ii) constant elasticity between capital and labor, and (iii) the possibility of different elasticities for different industries." They named it the CES function and estimated it across industries and countries.
One of the co-authors, Minhas1962, tried to rename it the "homohypallagic" function, deriving from Greek homo=same and hypallage=substitution. He credited the idea for this name to Emmanuel G. Mesthene of the Rand Corporation. The name did not catch on. Mukerji (1963) also tried to rename it the "SMAC function," using the initials of the four authors of Arrow et al. (1961) -- Solow, Minhas, Arrow, and Chenery -- but that too failed to catch on. The CES function did not play a major role in international trade theory during the first decade or two after its introduction, perhaps because trade theorists had a proud tradition of deriving results without specifying functional forms. It came into its own, however, in the Dixit-Stiglitz function used by Krugman (1980) as central to incorporating monopolistic competition into the New Trade Theory. The innovation there was to make the number of products (interpreted as varieties) variable. | |
| Comparative advantage | |
|
Ruffin (2002) credited the concept of comparative advantage and the law of comparative advantage to Ricardo (1951-1973), in a discovery that Ruffin dated to early October 1816. The law was developed in Ricardo's celebrated chapter on foreign trade, while the term comparative advantage seems to have first appeared in a later chapter (Ricardo (1951-1973), Vol I, p. 263). In crediting Ricardo, Ruffin disagreed with Chipman (1965) who credited Torrens (1815). From what I see in this debate, Torrens deserves credit for first stating the possibility that a country will import a good in which it has an absolute advantage, even though he seemed not to have recognized its importance, and he certainly did not work out the full conditions needed for this to happen, as Ricardo did.
| |
| Concertina tariff reduction | |
This term was introduced by Corden (1974, p. 370) who suggested it as an "optimal path of tariff reduction":
Calling this the concertina method seems slightly inappropriate, as players of concertinas squeeze the instrument from both ends, not just one. Indeed, Gruen (1993, pp. 15-16) contrasts Corden's "'Tops down' reform, or what Corden has called 'concertina method' tariff dismantling" with a combination of "both 'tops down' and 'bottoms up'" reform, which involves simultaneously raising the lowest tariffs. He notes that the latter is "more in keeping with the image of the concertina!" Most authors have followed Corden in applying the term only to 'Tops down' reform, probably because it can be shown to be unambiguously welfare improving if all goods are net substitutes. The alternative, of lowering the highest tariffs and raising the lowest -- and thus reducing their variance -- has been mentioned much less frequently, such as by Falvey (1994, p. 176) and Neary (1998, p. 188). Bleaney and Fielding (1995, p. 185) actually allude to it as being preferred -- as a policy though perhaps not as a term -- by the World Bank:
| |
| Continuum of goods | |
|
The first to model trade with a continuum of goods were Dornbusch, Fischer, and Samuelson (1977), who also used that term in their title. They cited an unpublished paper by Charles Wilson, also dated 1977, that further explored their model, but in the published version of that paper, Wilson (1980) credited them with having suggested this modification of traditional trade theory. This approach was admired but not used extensively by others until Eaton and Kortum (2002) replaced deterministic continuous functions for productivity with stochastic distributions in what is now the widely used EK Model.
| |
| Convergence play, Convergence trade | |
|
These two terms first appeared in 1993 in explaining the ERM Crisis motivated by expectations that interest rates would converge while exchange rates would not change, as intended by the convergence criteria.
In 1993, the IMF issued the multi-authored report Goldstein et al. (1993), Chapter III of which was titled "Prologue to the ERM Crisis: 'Convergence Play'". Discussing "the large, cumulative inflows of capital into the higher-yielding ERM currencies," the report goes onto say:
The other term, convergence trade, also appeared at this time, and the first I find is in Group of Ten (1993), Section III of which "discusses developments during 1992 in exchange markets and international capital markets, including the role of so-called convergence trades in the exchange market turbulence."
Neither of these sources stresses the importance of convergence of interest rates that presumably played an important role, both in the phenomenon and in the naming of it. Interest rates in Europe were intended to become more similar as part of the Maastricht Criteria. If that was expected, buyers of high-yield bonds could expect those interest rates to fall and the prices of their bonds to rise, making a capital gain larger than simply the higher interest rate. Svensson (1994) explained this better than most:
In an effort to see which of these terms is used more often, I asked NGram to plot "convergence trade" and "convergence play," but the former did not find anything, for some reason. Instead, the following is the plot for "convergence trading" and "convergence play", which suggests, perhaps incorrectly, that convergence play has been the more common and lasting.  The use of both of these terms has diminished, and they have been replaced by carry trade. | |
| Currency area | |
|
Mundell (1961, p. 657) spoke of "...defining a currency area as a domain within which exchange rates are fixed...". Perhaps because the exchange rates among separate national currencies are seldom if ever truly fixed, the term has come to mean a group of countries that share a common currency. Mundell also coined the term "optimum currency area" which is now more commonly expressed as optimal currency area.
| |
| Deadweight loss | |
This term for the efficiency costs of a tariff or other market imperfection was introduced to the literature by Samuelson (1952, p. 294):
The latter appeared in Samuelson (1960) in which he honored Harold Hotelling. Perhaps coincidentally, Hotelling (1938) is one of two sources that I came across that used "dead loss" to mean the efficiency loss due to a tax. This suggests to me that Samuelson may have introduced deadweight loss as an improvement over "dead loss," since the latter is used with other meanings in other contexts. Because of that, I've found it difficult to search for others who may have used "dead loss" with this particular economic meaning (more commonly it simply means an activity that is not successful). But I did happen across Bickerdike (1906) who used it precisely for the triangle of unrequited consumer loss due to an import tariff:
Whatever may have motivated Samuelson, his use of the term certainly caught on. Whereas my search for the term prior to 1950 found nothing, and in 1951-1960 found only the several articles by Samuelson, in 1961-1970 it appeared 26 times, almost all by authors other than Samuelson and with his meaning. There is less consensus on whether to render the term as 1) deadweight loss, 2) dead-weight loss, or 3) dead weight loss. Samuelson himself, in Samuelson (1960), used both the first and the second on the same page (p. 24). A Google-Scholar search over 1970-2016 finds more than twice as many of the first (17,600) as of the second and third combined (7,580).
| |
| Depression, The Great Depression | |
|
Mendel (2009, an intern at the History News Network, reported that the term depression was being used for an economic downturn as early as US President James Monroe in 1819, referring to what has been called the Panic of 1819 and its bank failures and currency depreciation. Monroe also used the phrase great depression in his 1820 Fourth Annual Message. Other presidents after Monroe -- including Grant, Hayes, and Coolidge -- used the terms as well, prior to Herbert Hoover, who is often credited with introducing the term in preference to the more common "panic."
Although Hoover referred to the world has experiencing "a great depression," he did not give it the name The Great Depression. That seems to have been coined by Robbins (1934). | |
| Dirty tariffication | |
|
The first use I find of this term is in a 1992 book that I will not add to my bibliography because I'm not sure of who the authors are. It is called FAIR TRADE IN BANANAS? International trade policies in bananas and proposals to alter existing policies in line with the Single European Market from University of Exeter, December 1992. It lists as editors Professor John McInerney and the Lord Peston, and as "contributors" David Hallam and Steve McConiston. Since I find no clear use of the term after that until 1994, followed by many uses in 1995, I'm inclined to credit the author(s) of this document, whoever they are, with coining the term.
The clearest explanation of the term that they provide connects it clearly with the use of tariff rate quotas, as in my definition #2. In footnote 8 on their page 37 they explain
| |
| Diversification cone | |
|
Dixit and Norman (1980, p. 52) attributed this to Lerner (1952) and McKenzie (1955). I see nothing in Lerner to justify this. McKenzie, however, made considerable use of the concept in the form of a set of factor endowments within which factor price equalization occurs, though he did not give it a name. Since he projected factor requirements and factor endowments onto a simplex, his set appeared as a triangle, though a cone was implicit. I do not yet know who may have preceded Dixit and Norman in using this term.
| |
| Dixit-Stiglitz utility | |
This refers unambiguously to the model of monopolistic competition introduced by Dixit and Stiglitz (1977) and to the similar model of Spence (1976) that led this sometimes to be called Spence-Dixit-Stiglitz utility. What is less clear is exactly what is meant by either term. The term Dixit-Stiglitz utility did not appear in publication until 1987, when it then appeared more than once but with slightly varying meanings. The varying meanings have continued since then, but the commonality among them is
Dixit and Stiglitz (p. 298) started with a somewhat general form for utility, u=U(x0,V(x1,x2,x3,...)), where the range of products was left unspecified but greater than the number of products actually consumed, n. They then considered several special cases, the one usually adopted by others being a CES form for the function V: u=U(x0,{Σinxiρ}1/ρ). What was crucial and distinctive about either form was that the number of products (often called varieties) consumed, n, was variable. Neary (2004) noted that later users of Dixit-Stiglitz utility combined three assumptions that Dixit and Stiglitz themselves mentioned but never used in combination: symmetry of V in xi, CES form for V, and Cobb-Douglas form for U. He therefore suggested that the following should be called "Dixit-Stiglitz lite":
In fact later users have often omitted the numeraire good, x0, or replaced it with other goods. And the symmetric CES function with variable n has, by itself, come to be what is most commonly regarded as the Dixit-Stiglitz utility function, or sometimes the Dixit-Stiglitz subutility function. In that case the Dixit-Stiglitz utility function appears identical to the CES function, the only difference being the interpretation of n as variable. The function has also been used frequently for production, with the xi as intermediate inputs, following Ethier (1982). The number of varieties was again variable and contributed to the value of the function, which in this case was output. However, Ethier made the role of n in productivity explicit with a second parameter, and his production function was:
| |
| Dumping, Anti-dumping | |
|
The word dumping began to be used in 1903 with essentially its current meaning of an unfairly low export price. Prior to 1903 the word was seldom used in the context of international trade (based on my Google Scholar search), and then primarily in combination with another word, such as "dumping ground" or "dumping field," in speaking of disposal of surplus product.
The term came into frequent use in 1903 in several books that were published in that year, such as Ashley (1903), and especially in the speeches of Joseph Chamberlain. In a speech on tariff reform in Liverpool on October 27, 1903, he defined dumping and stressed its harm to free-trade Britain:
Although the definition of dumping is today codified in the WTO and in national anti-dumping statutes, its definition has been subject to some dispute. Viner (1923) examined several alternative definitions and concluded in favor of "price discrimination between national markets" (p. 3). This deliberately included selling for different prices in different foreign markets and selling at home for a lower price than abroad. He called the latter practice "reverse dumping," and then had to identify the more common opposite practice as "export dumping." Finger (1993), who has argued that any industry can secure anti-dumping duties if there is political will, prefered to define dumping as "whatever you can get the government to act against under the antidumping law" (p. vii). The first anti-dumping law was enacted in Canada in 1904, as part of amendments to the Customs Tariff Act of 1897, according to Ciuriak (2005). As reported there, the legislation made no use of the words dumping or anti-dumping. and merely provided that imports should be subject to a "special duty of customs equal to the difference between such fair market value and such selling price." The first use that I've found of anti-dumping was Shortt (1906), writing about the Canadian policy. That the term caught on may not be surprising, but note that the other WTO-permitted unfair trade policy, directed at subsidized exports, is called a countervailing duty, not an anti-subsidy duty.
| |
| DUP activity | |
|
Bhagwati (1982) introduced this acronym for directly unproductive profit-seeking activity. After listing a variety of activities that fit this description, including rent seeking, revenue seeking, and others, he said (p. 990), "Thus, these are aptly christened DUP activities."
| |
| Dutch disease | |
|
Term was coined by The Economist in an article "The Dutch Disease" in the issue of November 26, 1977, pp. 82-83, which included the passage "... in the words of Lord Kahn [1905-1989], 'when the flow of North
Sea oil and gas begins to diminish, about the turn of the [21st] century, our island will become desolate.' Any disease which threatens that kind of
apocalypse deserves close attention." The article attributed the problems of the Dutch economy (an external appearance of strength but internally high unemployment and a declining manufacturing sector) to "three causes, only one of them external." These are (1) a strong currency; (2) high industrial costs; and (3) use of government gas revenues to increase spending rather than investment. As used since, the term has been focused primarily on the real exchange rate. The term was used by Corden and Neary (1982), whose reference to it as "... sometimes referred to as the 'Dutch Disease'" suggested that it had passed into common usage.
| |
| Economic weapon, the | |
|
Mulder (2022) said as he discussed the UK's Advisory Committee on Trading and Blockade in Time of War, "Its Legal Subcommittee included Cecil Hurst, the Foreign Office legal adviser who was probably the first to use the term 'the economic weapon' in 1912." Since Mulder wrote the book on the topic, he's likely correct, and I find nothing to indicate otherwise.
Google Scholar finds only two occurrences of the economic weapon prior to 1912, and these were both in the context of industrial-labor relations, where the term refered to economic actions such as strikes that workers might use against their employers. The first occurrence I find of the term meaning an economic substitute for military action against other countries was Adams (1915, p. 219):
| |
| Edgeworth-Bowley box | |
|
The origins of this were examined by Tarascio (1972). The diagram was first drawn by Pareto (1906), based originally, though only very partially, on a diagram of Edgeworth (1881). Edgeworth's diagram was not a box at all, and was drawn on axes more approptiate to an offer curve than to exchange of fixed quantities of goods or factors. Edgeworth's purpose was to define and depict the contract curve, which today we almost always draw within the box diagram.
Bowley's name was added to the name of the diagram as a result of Bowley (1924), who drew indifference curves for two individuals, one rotated clockwise 90 degrees and the other counterclockwise, thus forming the outline of a box, within which he showed Edgeworth's contract curve. That is probably why his name came to be associated with Edgeworth's. However, Bowley did not claim originality, and while he cited Edgeworth for the contract curve, he neither named nor attributed the box diagram. Indeed, in his own diagram showing exchange, his focus was on the internal portion and he did not extend the axes of his two indifference maps far enough to touch or cross, and therefore did not actually produce a box. Had he done so, his box would have been a mirror image of the one we normally draw today. It was Pareto (1906), writing in Italian that was soon translated into French, who had actually been the first to draw and use the box diagram. It is unclear whether his contribution was known to Bowley and to others writing in English until later. His diagram, displaying indifference curves for two consumers, one drawn conventionally and one rotated 180 degrees, formed the box very much as we know it today, for exchange between consumers. With each consumer endowed with only one of the two goods, he showed a trade equilibrium as a common tangent to two indifference curves that were also tangent to a price line from the consumers' endowment point. I have searched in Google Scholar for "Edgeworth box," "Edgeworth-Bowley box," "box diagram," and the joint appearance of "Edgeworth" and "box." The last of these gets many hits, of course, but none of them were about the Edgeworth box, until Stolper and Samuelson (1941). Their Figure 2, p. 67, had labor and capital on the axes and isoquants for two industries inside. Of this they said:
Based on all of this, it appears that the box applied to consumption, as well as the Edgeworth production box, have both often been called just the Edgeworth Box, even though Edgeworth never drew either. Calling it the Edgeworth-Bowley box is only slightly less erroneous, since Bowley's version of the box was incomplete and perhaps accidental. Pareto was more deserving of having his name on the consumption version of the box diagram than either Edgeworth or Bowley. Stolper and Samuelson, if they needed further recognition, should share credit for the application to production that has played such a large role in international trade theory. And it seems likely that they, too, were the ones who led us to call it the Edgeworth or Edgeworth-Bowley box ever since.
| |
| Emerging market | |
|
According to The Economist (October 7, 2017), "The term was coined by Antoine van Agtmael in 1981 when he was working for the International Finance Corporation (IFC), a division of the World Bank." As explained there, he pitched the idea of a "Third World Equity Fund" -- which would give foreign investors easier access to stock markets in places like Brazil, India, and South Korea -- to a group of fund managers. Some were intrigued, but hated the name. "So Mr Agtmael spent the weekend dreaming up the term ''emerging markets', with which he hoped to evoke 'progress, uplift and dynamism.' That label proved wildly successful."
| |
| Flying Geese | |
|
The name Flying Geese Model or Paradigm derived from a graph of Akamatsu (1961), (but 1937 in Japanese) that resembled a formation of flying geese. The graph showed paths over time of a developing country's imports, production, and exports of a product, similar to the product cycle.
| |
| Fragmentation | |
|
As used to mean a splitting up of production processes, the term fragmentation was first introduced by Jones and Kierzkowski (1990), who started their analysis by noting (p. 31) that increasing returns and specialization encourage a growing firm to "switch to a production process with fragmented production blocks connected by service links.... Such fragmentation spills over to international markets." [Italics in original.] Many other terms have been used with the same, or related, meanings, as listed here, but fragmentation seemed to have caught on most widely in the 1990s academic literature. More recently, a more common choice seems to be global value chain, or just supply chain, even though these seem to connote a more linear succession of inputs-to-inputs-to-inputs, rather than a splitting up into multiple inputs at the same stage of production.
| |
| Gravity model | |
What we now call the gravity model of bilateral international trade flows first appeared independently in Tinbergen (1962) and Pöyhönen (1963), but neither used the word gravity. Tinbergen's formulation was very similar to the formulation of the basic model used today:
Pöyhönen was member of the same Finnish research team as Pulliainen (1963) whose formulation was more like Tinbergen's. While he also did not call this a gravity model, he did mention the parallel: "The results of our empirical study show that the structure of international trade is capable of description in terms of gravitational theory." (p. 88). This analogy to gravity was actually resisted by another early user of the model, Linnemann (1966), on the grounds that force of actual gravity falls with the square of the distance between objects. He followed the above authors in setting out an equation much like the above, with Y's replaced by "potential supply" and "potential demand" which he went on to explain in terms of both GDP and population. But in his footnote 43 (pp. 34-35) he remarked, "Some authors emphasize the analogy with the gravitation law in physics, and try to establish that [α3=−2]. We fail to see any justification for this." And in the rest of his book the only mention of gravity regards the "centres of gravity" of the countries considered, used for defining distance between them. The first to call this a gravity model seems to have been Waelbroeck (1965), which included (p. 499) "Hypothesis 2: The gravity model: distance, export push, and import pull" and has the equations from the other three authors. Waelbroeck notes that "There is, as has been pointed out, an odd similarity between formulae (6) and (7) and the law of gravity, with Yi and Yj playing the role of masses, and this justifies christening the model as the gravity, or G, model." He did not say where it was "pointed out," but it seems likely that he was referring to Pulliainen (1963). Predating all of this explicit application to bilateral trade between countries, however, the term gravity model was used in other social science contexts, and models of this form were used, under other names, in other applications. Bramhall and Isard (1960), in a chapter of a volume on regional science, discussed "gravity, potential, and spacial interaction models -- which for short we shall term gravity models." Similar to other earlier applications that do not seem to have used that name, they formulated the number of trips between areas with different populations, using populations instead of GDPs. Another later source, Glejser and Dramais (1969), cited gravity models as having been used for a long time in literatures on migration, tourism, and telephone calls as well as trade. In a series of papers starting with Zipf (1946), Zipf applied what he called "The P1P2/D Hypothesis" to inter-city movements of freight, persons, information, and perhaps more. Stewart (1947) included in his "Empirical Mathematical Rules Concerning the Distribution and Equilibrium of Population" a formula similar to gravity, but called it "potential." He also cited a much earlier author, Reilly (1929), who provided a "law of retail gravitation," but that was for explaining the market regions covered by cities of different sizes, not the transactions between them.
| |
| Great Moderation | |
|
This term, as applied to the moderating of economic fluctuations from the 1980s to 2007, seems first to have been used by Stock and Watson (2003). They used the word "moderation," not capitalized and without the adjective "great," throughout the paper, but the title of their section 3, p. 170, was "Dating the Great Moderation."
The term was picked up, and probably made much more visible, by Ben Bernanke in his Remarks at the meetings of the Eastern Economic Association in Washington, DC, February 20, 2004, when he was a member (but not yet Chair) of the Board of Governors of the Fed. See Bernanke (2004). He cited several authors as having documented the decline in volatility, the first being Kim and Nelson (1999) who cite McConnell and Perez-Quiros (2000), in a 1999 Fed working paper, as having documented the decline in a linear formulation rather than a structural shift. McConnell and Perez-Quiros, in turn, started their paper with "The business press is currently sprinkled with references to the 'death' or 'taming' of the business cycle in the United States." Neither of these papers used the term Great Moderation, or even the word moderation. So it appears that the phenomenon represented by the Great Moderation was noted gradually over time and then documented by a number of scholars. The name for it as well as one of the more rigorous documentations of it were by Stock and Watson (2003).
| |
| Grexit | |
|
This term first appeared in print in Buiter and Rahbari (2012). DeTraci Regula, in an undated posting on About.com, suggested that the term was coined by the second author, Citigroup's Ebrahim Rahbari. She also pointed out the prior existence of GrexIt.com, an e-mail storage and organizing tool. I was told by someone who worked in the EU prior to 2012 that the term was in use there as early as 2010.
| |
| Harberger triangle | |
|
As a theoretical construction for measuring welfare costs due to market distortions, this idea goes back to Dupuit (1844) and independently to Jenkin (1871-72). Dupuit, pp. 280-282 in the 1969 reprint, very clearly explained how to infer utility from the area to the left of his demand curve (which has price on the horizontal axis), then used that to derive the triangle of net loss from a tax in his Figure 3. Jenkin, p. 113, provided a supply and demand diagram much as we would use today (albeit with the axes reversed and with curves, not straight lines) and also the incidence and welfare effects of a tax. He clearly identified what we would today call the excess burdens of the tax on suppliers and demanders, using the familiar (curvilinear) triangles: "This excess of loss is represented by the area CC"D for the sellers, and C'C"D for the buyers."
Hines (1999) provided a good review of this history. Although several others had used this tool, Arnold Harberger made repeated use of it especially in Harberger (1954) applied to monopolies, in Harberger (1964a) applied to an excise tax, and in Harberger (1964b) applied to other distortions. Although Chase (1964) referred twice to "Harberger's triangle," he did so in an edited volume where he was summarizing another of Harberger's papers that appeared there. The term Harberger triagle then did not appear in print, that I can find, until 1976, even though several authors cited Harberger's papers and his method. Then, in 1976, Bruno and Habib (1976) included
Harberger triangles in trade
For some reason, however, trade economists have tended to prefer the term deadweight loss to identify the costs measured by Harberger triangles in the tariff context.
| |
| Hirschman index | |
|
This index of trade concentration first appeared in Hirschman (1945). Michaely (1958) misunderstood it as being identical to the Gini coefficient and called it that in his application to exports, while acknowledging that Hirschman had also used it for that purpose. In fact Hirschman's formula, H=sqrt[Σ(xi/x)2], is not the same as the Gini coefficient. As Hirschman (1964) pointed out, his formula reflects not just unequal distribution but also fewness, its value rising the smaller is the number of goods in the summation. I have calculated both measures in a spreadsheet and can confirm that they do indeed yield different values and that the Hirschman index does indeed fall as the number of goods rises, while the Gini coefficient does not. In spite of this, several others followed Michaely in calling it the Gini coefficient or Gini index, until Hirschman published his correction in 1964.
Hirschman (1964) also pointed out that his index differed from what had come to be called the Herfindahl index of industrial concentration only by Hirschman's inclusion of the square root. Herfindahl had introduced his index in Herfindahl (1950). In spite of the fact that Herfindahl himself acknowledged Hirschman's prior contribution, his index was named the Herfindahl Index by Rosenbluth (1955) and the name stuck, even though Rosenbluth later tried to correct the error. Today (June 2022), the Herfindahl index is said by Wikipedia to be "also known as Herfindahl-Hirschman index, and there is no entry at all for Hirschman index." Interestingly, NGram finds Hirschman index used most frequently since 1983, with Herfindahl used most frequently prior to that. Use of Herfindahl-Hirschman index parallels Hirschman index, but somewhat below it. I suspect that NGram includes Hirschman in its findings for Herfindahl-Hirschman. If so then it is clearly Herfindahl-Hirschman that has been most widely used since 1983. 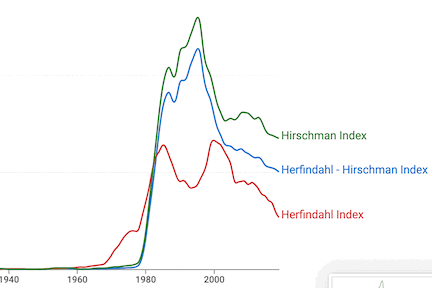
As for the Hirschman index itself and its use for quantifying concentration of trade, it is difficult to search for it in Google Scholar without the Herfindahl, but I was able to find a few sources that used it. For example, Ng (2002), p. 587 said "The related measure used by UNCTAD is the concentration index, or Hirschman index (H)" and then provided the formula above.
| |
| Holy Trinity, Inconsistent Trinity, Impossible Trinity, and Trilemma | |||||||||||||||||||||
These four terms -- and probably more that I haven't seen yet -- have each been used in the literature of international finance to mean the impossibility, or at least the difficulty, of achieving the following three aims simultaneously:
The first to be used for something like this was trilemma, which I only learned about belately. Maury Obstfeld directed me to a passage in Irwin (2012), who had been alerted by Russell Boyer to an early draft of Friedman (1953). It, in a passage not included in the published version, said that the macroeconomic dilemma
The term holy trinity was used with this meaning, but perhaps only once, as it mostly had other meanings even within international macroeconomics. The second, inconsistent trinity, appears to have been the first to be used more than once in published work, in response to the monetary crisis of 1971. The third, impossible trinity, and especially the fourth, trilemma, have been used with this meaning a great deal in recent years. I will deal with each in turn.
Holy Trinity
The second threesome concerns the policy arrangements that may be used to achieve one or more of these attributes:
The earliest use that I have found for Holy Trinity in the context of international monetary economics was a doctoral thesis, Høiberg-Nielsen (1983). This included (p. 116-117),
The term Holy Trinity is of course widely used in a religious context, and also in many other contexts where a threesome is thought to be especially important. In economics, for example, Machlup (1965) and at least one other used it for the "objectives of a stable price level, full employment, and a faster growth rate." My search for the term in Google Scholar is hindered by its wide use in other contexts. But I have looked for it, as well as the other terms considered here, in some of the more widely cited works of both Mundell and Fleming, and I failed to find it. My expectation that I would find it in Mundell was prompted by Rose (1994) who said (p. 1) "This paper is concerned with the compatibility of: fixed exchange rates; independent monetary policies; and perfect capital mobility, Mundell's 'Holy Trinity'." Note though that Rose uses Holy Trinity for the problematic threesome of policies, not the threesome of attributes. I have yet to find any earlier source for this interpretation. On the contrary, I found Eichengreen (1993, p. 621) saying, "In the 1960s and 1970s, most of the literature on the Bretton Woods system was organized around the holy trinity of adjustment, liquidity, and confidence." One might have expected Rose and Eichengreen to agree on the use of the term, since they were both at Berkeley, but apparently they did not. Eichengreen cited Mundell (1969), which did include a section headed "Liquidity, Adjustment, and Confidence," but Mundell did not mention any trinity, at least in that source.
Inconsistent Trinity
Given his prominence -- Wallich had been a member of the US President's Council of Economic Advisors and was later a governor of the Federal Research Board -- I'm not surprised that his use of the word trinity for this threesome led others to use it, even if some may have also called the trinity "holy."
Impossible Trinity That the Impossible Trinity was the policy threesome was confirmed by Frankel (1994), who cited Reisen, and also by Borensztein and Ostry (1994) who did not. So at least until I can confirm from the source that Reisen used the term for the policy threesome, I am comfortable attributing it to him for its current use. Since his own publication seems to be a bit obscure, I am inclined to credit others, such as Rose and Frankel, for the term's subsequent popularity.
Trilemma My own search failed to find it before 1997, but again Maury Obstfeld alerted me to his paper Obstfeld (2020) where he cited columns by Friedman both in Newsweek, Friedman (1979), and in The Economist, Friedman (1983), that used the term. It was unclear in the first of these that this was the same trilemma discussed here, but in the second it was very clear indeed:
I found trilemma first in scholarly published work with its clear current meaning by Obstfeld and Taylor (1997). They said (p. 2):
To sum up, based on the sources that I have learned of, the four terms were introduced into the scholarly literature of international finance, with the current meaning of the threesome of policies above, by the following:
| |||||||||||||||||||||
| Home market effect | |
|
This effect was both introduced and named by Krugman (1980), so there is not much more to say. However, Krugman spoke on p. 955 of "'Home Market' Effects," plural, suggesting that there may be more than one. The two effects that he demonstrated were the following:
First, in a model with increasing returns to scale (IRS), p. 957;
It is worth noting also, as Krugman did in his final sentence, that these results were anticipated by Linder (1961) and by Grubel (1970). Linder did stress the importance of the demand in the home market in order for a country's industry to succeed and export (p. 17): "...a country cannot achieve a comparative advantage in the production of a good which is not demanded on the home market." But rather than stressing IRS, he viewed production functions as differing across countries in response to differences in demand (p. 90): "... the production functions of goods demanded at home are the relatively most advantageous ones." And Linder never spoke of a home market effect. Grubel, in a larger discussion of intra-industry trade, considered products differentiated by quality, with low-quality goods demanded more by low income consumers. Allowing then for IRS as well as differences in the distribution of income across countries, he noted that a country with a preponderance of low-income consumers would "specialize in the production of the low price and low quality model, supplying its own population and exporting to meet the demands of [the other country's] population with below average income."
| |
| Hub and spoke integration | |
|
Once countries began to enter free trade agreements with multiple other countries that did not have FTAs among themselves, it may have been inevitable that this arrangement would come to be called hub-and-spoke integration. The first use of hub-and-spoke in this context that I have identified was Wonnacott (1990), which included it in the title. The paper itself is no longer available, at least that I can find. I therefore don't know whether Wonnacott merely used the term to describe these arrangements, or went beyond that to formulate an economic model of this sort of integration.
Such a model was certainly provided by Puga and Venables (1995) who also included hub-and-spoke integration as a keyword for their paper. They also cited Baldwin (1994) as discussing such arrangements, although again, as I have so far been unable to access Balwin's book, I don't know whether he even used the term or provided a model. Baldwin was cited by one author, Stawarska (1998), as "the author of the hub and spoke integration model."
| |
| Ideal price index | |
|
There are two widely used things that are routinely given the name ideal price index. The oldest is the square root of the product of the Paasche and Laspeyre price indexes:
The second item that has come to be called an ideal price index is what can be derived from an explicit utility or production function as the minimum cost, given the set of individual prices of goods or inputs, of a unit of utility or output. The specific formula therefore depends on the utility or production function chosen, but most commonly in recent years these have been assumed to be CES, often with a variable number of arguments as in the Dixit-Stiglitz function. The arguments of this function can be countable, but most often today they are taken to be in an uncountable set, over which both objective function and ideal price index are integrals. For example, using the notation of Bergstrand et al. (2019), let utility in situation i (year, country, etc.) be The term ideal price index has been used for objective functions ranging from Cobb-Douglas, through 2-good and n-good CES, to functions like this with additional arguments for other categories of goods. So unlike Index above, there is no single agreed-upon formula for this version of the ideal price index. Interestingly, this second version, despite its name, is not really an "index" at all in the usual sense. Indexes are needed when a simple average would not be meaningful, as when averaging across items with different units of measurement. Thus the initial Index above in necessarily a ratio, comparing prices across two situations. Neither numerators nor denominators within the expression have any meaning by themselves, but only in relation to their counterparts. In contrast, Pricei is defined for just the single situation i. If the objective function is a production function, then it is the minimum cost of a unit of output, which is well understood. But if it is a utility function, then it is the cost of a unit of utility, which has never been intended to have meaning by itself. Therefore, what is today routinely called an ideal price index only becomes an actual price index when used in a ratio, such as (Pricei / Pricej), comparing prices in two different situations. It should be noted, too, that even this ratio will only be meaningful if the utility or production functions from which Pricei and Pricej are derived are linearly homogeneous and therefore, for utility, homothetic. Now where did all this come from? For the older Index, that is fairly easy. It was Fisher (1922) who suggested and named it, though the formula itself had been suggested much earlier by Bowley (1899). Bowley called it (p. 641) "The best method theoretically for measuring 'aisance relative'." Aisance in French apparently means ease or affluence. For decades after Fisher named it, the square-root formula has been used and usually referred to as the "Fisher ideal price index." The first effort I have seen to try to do better than Fisher by deriving a measure of prices from an objective function was Samuelson and Swamy (1974). They continued to use the term ideal price index but only for Fisher's formula, not for their own. To improve on this, they defined by a price index and a quantity index from general objective functions, and showed them to be dual to one another. Samuelson and Swamy do not call their own indexes "ideal." Recognizing instead their dependence on scale or income, they say (p. 568)
Most often cited by those who use things like Pricei above are Sato (1976) and Vartia (1976), whose Sato-Vartia weights allow them to give appropriate weights to different prices. Both Sato and Vartia did call their indexes "ideal," but as "ideal log-change index numbers" and, in the case of Sato, an "ideal log-change price index." Neither spoke of an ideal price index without the "log-change" qualification. Vartia referenced a 1975 discussion paper by Diewert that also deals with "ideal log-change index numbers." Diewert (1978) later examined several alternative price indexes, including what he called the Vartia index, but he used the word "ideal" only for the Fisher index. And in later work he showed that the Fisher index would be what he called "exact," for a unit cost function that is quadratic. His "exact" seems to be what is now called "ideal," in that it can be derived from a specified objective function. Considering the role of the Pricei form of the ideal price index in measuring the importance of variety for welfare, one might have expected it to have been derived by Dixit and Stiglitz (1977). They did indeed derive it (for a sum of varieties, not an integral), and they called it a "price index," but they did not call it "ideal." It is only in 1985 that I find sources using the term ideal price index with the meaning of Pricei. Both Obstfeld (1985) and Jagannathan (1985) used the term and attributed the idea to Samuelson and Swamy (1974), even though neither those authors -- nor any since that I can find -- had used the term in print. From the published record, I cannot infer who among all these authors and others may have begun using the term in conversation. The term has certainly caught on in recent years, but interestingly it was not used in two of the most influential papers that used the concept itself. Feenstra (1994) and Broda and Weinstein (2006) -- both known for using it to quantify the benefits from increased variety due to international trade -- used the index but not its name. Feenstra (p. 158) spoke of an "exact price index for the CES unit-cost function." Broda and Weinstein followed Feenstra in calling it the "exact price index," and used ideal price index only for the Fisher formula. Well before Broda and Weinstein (2006), however, I find numerous uses of ideal price index to mean something like Pricei, and I find even a few before Feenstra (1994) such as Obstfeld (1985) and Jagannathan (1985) mentioned above. By now the term seems to have become far too standard for most authors to mention any source or sometimes even to explain it. As just one example, I went through the 37 appearances of ideal price index found by Google Scholar for the year 2003, and eleven of them were a variant of Pricei. I have not done the same for very recent years, as the term is now used more than 100 times each year, still often with the qualification "Fisher," but also often without and presumably something like Pricei.
| |
| Immiserizing growth | |
|
The term "immiserizing growth" was used by Bhagwati (1958) and it seems unlikely that anyone used it before him, since he seems to have coined the word "immiserizing."
As for the concept, Bhagwati credited Johnson (1953, 1955) with identifying a form of immiserizing growth and also with working out the conditions for Bhagwati's form of it in an unpublished note. Long before both of them, Edgeworth (1894, p. 39-40) had shown, though only by example, that increased production of exports could so reduce their relative price that the country would lose or, as Edgeworth put it, be "damnified by the improvement." Perhaps he should have called it "damnifying growth." Edgeworth in turn credited Mill (1821) with noting the possible worsening of the terms of trade, although Mill apparently incorrectly equated this worsening with a necessary decline in welfare. (I have not read Mill and am taking Edgeworth's word for this.)
| |
| Infant industry protection | |
|
Several sources cite Alexander Hamilton (1791) as the first to argue in favor of tariffs to protect infant industries, on the grounds that their costs are initially so high that they will only be able to compete if protected, and that they will then be able to reduce their costs sufficiently to prosper without assistance. Hamilton's purpose was indeed to argue both for the importance of manufactures and for the need to use policy to promote manufactures. However, in parts of this document he stated a clear preference for using "bounties" -- i.e., subsidies -- for this purpose: "...they are, in some cases particularly in the infancy of new enterprises, indispensable." (p. 280) Elsewhere, speaking specifically of encouraging production of iron, he favored a tariff: "The only further encouragement of manufactories of this article ... seems to be an increase of the duties on foreign rival commodities."
Some have also cited Say (1803) as an early advocate of infant industry protection. I have searched that document and do not find the basis for this. There is a discussion of reasons for using tariffs (mostly called "duties"), but none seems to capture the infant industry reasoning. Most cite List (1841), writing in German, as providing the first explicit case for infant industry protection, and this seems right. In Chapter 12 of the 1909 translation by Sampson S. Lloyd, he said:
It was Mill (1848) who made the case first in English:
The term "infant industry protection"
I find no further occurrences of the phrase infant industry until the period 1880-1885. Taussig (1883) made the case for what he only called "young industries," but I found four other authors, around the same time, referring positively or negatively to protection of "infant industries." Sumner (1985), for example, in his Chapter V on "Sundry Fallacies of Protectionism," listed his first as "That infant industries can be nourished up to independence and that they then become productive." The idea, together with the association with infant rather than young, new, or immature industries had become the standard term. Ely (1888), in a collection of articles originally written for the Baltimore Sun, devoted a chapter to "The Infant Industry Theory of Protectionism Further Considered."
The conditions for "infant industry protection"
| |
| Intermestic | |
I could have simply said due to Manning (1977) in the glossary entry for this word, but I can't resist quoting the passage where the author coined the term:
| |
| J-Curve | |
|
Magee (1973) seems to have been the first to do careful theoretical analysis of this phenomenon of the trade balance first worsening before it improves after a devaluation. But he was certainly not the first to use the term, as he cited a passage from the 1972 Wall Street Journal describing "what economists call a J-curve" in reference especially to the aftermath of the devaluation of the British pound in 1967.
A search through Google Scholar finds the term J-curve used frequently in other contexts, but the first use of the term applied to effects of a currency devaluation seems to have been at a 1971 conference (the proceedings of which I have not yet seen) and by Posner (1972). Both of these use the term as though it is already familiar, so I suspect that it had entered common use before this in the economic press.
| |
| Kaldor-Hicks criterion | |
|
Kaldor (1939) was the first to state this criterion, but he was followed in the next issue of the same journal by Hicks (1939) who built on Kaldor and developed the idea more fully. One could easily, based on reading Kaldor and the fact that Hicks did not claim to have had the idea himself, conclude that this should be called simply the Kaldor criterion. Several authors in the next few years did attribute it solely to Kaldor. Most notable was Scitovszky (1941), who pointed out that the "principle enunciated in Mr. Kaldor's first-quoted article" (p. 77, footnote 1) could in certain cases justify both a policy change and its reversal.
It was Little (1949a, 1949b) who first called it the Kaldor-Hicks criterion. In 1949a, he credited Hicks with going beyond Kaldor by explicitly using it as a criterion for an increase in welfare, and then, throughout the last half of the paper, called it the Kaldor-Hicks criterion. Later the same year Little (1949b) addressed Scitovszky's criticism, and used that terminology throughout.
| |
| Lerner diagram | |
|
The Lerner Diagram was first drawn by Lerner in an unpublished seminar paper (a "term paper" according to his teacher Lionel Robbins) in 1933. He used unit-value isoquants together with unit isocost lines to show the relationship between goods prices and factor prices in the H-O model. That paper was reproduced, "as it was originally written" according to the journal editor, as Lerner (1952). It appears that Findlay and Grubert (1959) were the first to make extensive use of the diagram, attributing it as "a diagram introduced by Mr. A. P. Lerner in his brilliant paper on factor price equalization in international trade." They did not happen to christen it the Lerner Diagram, however, and the first use of this (based on a Google Scholar search) was by Findlay (1971).
Some (including myself, until I learned better) have called it the Lerner-Pearce diagram, giving credit also to Pearce (1952). Bierwag (1964), in footnote 2, p. 57, said "This diagram is often called the Lerner-Pearce diagram..." citing Lerner (1952) and the Pearce's comment in the same issue of the the journal, and said "it has been widely used in international trade theory." That may be, but he cites only Findlay and Grubert (1959) plus the preface to the Japanese edition of Harry Johnson's International Trade and Economic Growth, which I have not attempted to find. In fact, although Pearce (1952) was debating Lerner regarding the likelihood of factor price equalization, he used unit isoquants, not unit-value isoquants, for the purpose. Since these do not align in equilibrium with a single unit isocost line, they cannot be used in the same way, and they do not achieve the essential simplicity of Lerner's construction. Pearce did use the diagram with unit-value isoquants in his comment on Lerner (1952), but there he wass clearly following Lerner.
| |
| Level playing field | |
|
This term in a general context means subjecting all participants in an activity to the same rules. Exactly how that came to be seen as leveling a field is not at all clear. In sports, a tilted playing field may well advantage one team or the other, but by changing direction at half-time, that advantage can be made even.
In the context of economics, I find the level playing field mentioned first for banking, and for financial markets more generally, as these were deregulated around 1980. As regulations were relaxed for some financial institutions, other institutions sought similar relaxation for themselves. These concerns extended especially to international financial markets, where differences in national regulations put some countries' firms at a disadvantage. I find no use of the term level playing field in the context of international trade until 1982, when Bergsten and Cline (1982) cited Cline as noting that as comparative advantages become small due to growing similarity of factor endowments and technologies, differences in government policies and regulations become increasingly important in determining trade. They then say (p. 24):
| |
| Marshall-Lerner condition | |
The condition was first stated in words by Marshall (1923) as characteristic of two offer curves that intersect in an unstable equilibrium, which he showed in his Fig. 20, p. 353 (appearing here as point E in Figs in the case Both Very Inelastic):
The next appearance of the condition was twenty years later still, in Lerner (1944). The context was very different from that of Marshall, as Lerner was not looking at the market for international exchange of goods. Rather, his purpose was to determine whether a mechanism for maintaining full employment through the gold standard would be stable. The mechanism would start with a fall in the price level due to the outflow of gold associated with a negative trade balance. To be successful, that fall in price level would need to reduce the trade deficit, thus increasing aggregate demand. But then he said, "There are other circumstances that render the automatic maintenance of full employment still more precarious." His reason was that the direct effect of a fall in prices is to decrease the value of a given quantity of exports, not increase it, and this then needs to be offset by sufficient increase in export quantity and/or decrease in import quantity in order to cause net exports to rise. For this to be true, he said,
A number of authors have chosen to name the condition after Robinson as well as Marshall and Lerner, presumably on the grounds that Robinson (1937) preceded Lerner in examining the same question of a devaluation and the balance of trade. Indeed, she did it more formally in a mathematical footnote that derived the change in the trade balance as
There is one other source that might have been expected to reach the result before Lerner (1944): Machlup (1939-40), who dealt in great detail with "The Theory of Foreign Exchanges." He applied supply-and-demand analysis to the exchange of currencies, and he noted that the supply curve for foreign exchange could be backward bending, changing some of market's comparative static implications. However, he did not mention that if both demands were sufficiently inelastic, then the equilibrium would be unstable. Therefore he did not find his way to the third familiar implication of the Marshall-Lerner condition: the stability of the market for foreign exchange. From all of this, the name Marshall-Lerner condition seems appropriate, since both of those authors stated the condition, independently and in different contexts, and no other author seems to have done so before them. Who gave it the name? Searching the literature around this time, I find Polak (1947) citing the condition, but only as "the well-known formula." Likewise Haberler (1949) presented the condition and included the following:
| |
| Meade Index | |
|
Meade (1955a) did not put his calculation into the form of an index, except in an appendix, but rather suggested adding up the increases in trade and the decreases in trade separately, each weighted by tariffs, and concluding that there had been a gain from trade (in his context of formation of a customs union) if the former were larger than the latter.
In his example of the duty on Dutch and Belgian beer, Meade said (p. 66):
Meade's main point was that one should not look only at the product on which the tariff is being reduced, but rather at all changes in trade that will be caused, both positive and negative, by that change. Of course if tariffs on all other products were universally zero, then the contributions to his calculation for them would also be zero. Hence, this is a simple way of taking account of the second-best nature of a tariff reduction when tariffs on other products are not zero. In his Appendix II (pp. 120-121), Meade formalized his calculation and called it "an index of the change in world welfare," which he derived as dU = uΣi{dxi(pi−ci)} where U was world utility, u was the common marginal utility, dxi was the change in trade of good i, pi was price to consumers, and ci was price (i.e., cost) to producers. It seems to have been Vanek (1965, p. 15) who first called this the Meade Index.
| |
| Mirror statistics | |
The technique of using one country's trade data to derive or check the trade data of a country with which it trades has probably been used as long as data on trade were being published and used. But the term for this, mirror statistics, is found first by Google Scholar in Brown, Marer, and Neuberger (1974), p. 300-301:
While the technique could be and probably is applied to data other than international trade, it is most frequently used for trade, and especially for trade with countries like the Soviet bloc and China where trade data, in the past, were unavailable or unreliable.
| |
| Most Favored Nation | |
|
The term goes back more than two centuries. The earliest use I've found with Google Scholar was from 1784, but the idea entered into international commercial treaties long before.
The term itself can be misleading, since when applied to a country it may be interpreted as favoring that country over others. In fact, the meaning is rather to not treat the country worse than others. It may have been this tendency to misinterpret that led the United States to replace the term with permanent normal trading relations in 1998, during the lead-up to granting China permanent MFN treatment in 2000. Erler (1956) said that the practice of treating trade partners no worse than others goes back to the 15th century. Erler wrote in German, so I thank my friend Willi Kohler for providing the following:
For instance, a treaty signed on August 17, 1417, by Henry V of England and Duke Johann of Burgundy stipulates that English captains shall be allowed to land their ships in Flemish ports "in the same way as the French, the Dutch and the Scottish captains would do." Erler explicitly (though perhaps not too convincingly) calls this an instance of MFN. [Erler (1956, p 52)] A further instance was the London Trade Agreement (sic! Londoner Handelsvertrag), signed on July 22, 1486 by Henry VII of England and Duke Franz of Brittany. It stipulates that English merchants, when doing business in Brittany, shall enjoy the exact same liberties/freedoms as do merchants from any other state who maintain commercial relationships with Brittany. Further, they shall be treated with the same "caution and graciousness" as these other merchants. This pretty much seems like true MFN treatment. [Erler (1956, p 53)] A source that I found online but have been unable to learn the author of (it seems to be a chapter from a dissertation in India) says that the concept of MFN has been used since the middle ages. But its first use by more or less that name was in the Treaty of Utrecht, which was actually a group of several treaties ending the War of the Spanish Succession 1713-1715. One of those, the Treaty of Peace and Friendship, included the following passage:
| |
| New new trade theory | |
This name, which is surely even more unfortunate than the "New Trade Theory," was introduced to the literature in 2004 by Richard Baldwin and co-authors. Baldwin and Forslid (2004) say the following (p.1):
| |
| New trade theory | |
|
This unfortunate term -- unfortunate because it has continued to be used more than forty years after the group of theories that it refers to were introduced, which are therfore not at all new -- may not have been introduced by any one person. Initially, it was simply used to distinguish what were then some recent theories from the older theories of Ricardo and Heckscher-Ohlin-Samuelson. But as no more descriptive or person-specific name came into use, new trade theory became the standard by default. This was surely at least in part because the new trade theory encompassed multiple models by multiple authors, their common characteristic being only that they included one or more of three departures from traditional assumptions: increasing returns to scale, imperfect competition, and product differentiation.
As I search for use of the term new trade theory in Google Scholar, I find nothing at all before 1984. In that year there was only one source that uses these words, Borrus, Tyson, and Zysman (1984), and it wasn't obvious that they thought this was a name for the recent literature but only a convenient way of directing attention to it. Only in 1986 do I find the expression appearing again, and now it showed up in five publications in that year. None of the authors in that year spoke as if they were naming this recent literature themselves. But as Krugman (1986a) used it several times, I am inclined to give him credit for popularizing the term. One other author, and in a volume edited by Krugman, spoke of "the so-called 'new' trade theory," perhaps having heard Krugman and others speak of it. For many, including perhaps Krugman himself, the new trade theory is most closely associated with his writings, even though many others contributed importantly to it. One might have expected that "Krugman" would have taken his place alongside Ricardo and Heckscher-Ohlin in the name for a trade theory. But that did not happen, perhaps because Krugman himself led with the term new trade theory. There is of course a Krugman Model, but that is only one among many models, by Kruman and others, that are included the the new trade theory.
| |
| Normal Trade Relations | |
This term was adopted in 1998 by the United States Congress to replace Most Favored Nation in certain US statutes. The legislation was signed by President Clinton July 22, 1998, shortly before the debate on MFN China renewal. As it was explained in Senate Report 105-82, "Clarifying the Designation of Normal Trading Relations," September 15, 1997,
Wikipedia once explained the change as follows, but gave no source (and it no longer appears):
| |
| Odious debt | |
The first use of this term seems to have been by Sack (1927), although as that book is in French, I cannot directly confirm that the term appeared there or that it appeared without reference to an earlier source. My basis for being fairly confident that this was the first use of the term with this meaning -- of debt that may be legitimately not paid back by a successor government -- is a footnote much later in Sack (1947) where he referenced that earlier work:
This does not mean that the concept in international law was new at that time. Cahn (1950) included a footnote covering almost a full page citing dozens of sources on the topic, only the last and most recent of which was Sack (1927).
| |
| Offer curve | |
The offer curve, without the name, was first developed by Alfred Marshall. It was first published in an Appendix attached to Book III, Chapter VIII, of Marshall (1923), but as he explained in an opening footnote,
He did not however name it. He referred to his curves throughout only as OE and OG, for England and Germany respectively. Only once did he even use the world "offer" in connection with these curves, saying "E will be prepared to offer only OM′′ of her bales in return for P′′M′′ bales from G." The best candidate I find for having named the offer curve is Edgeworth (1894). This article was published in three parts, in the second of which, Edgeworth (1894) Part II he showed the curves in various configurations and used the verb "offer" to explain what they represented. Then in the third part, Edgeworth (1894) Part III, discussing a similar diagram of Auspitz and Lieben (1989), he said "Accordingly their supply- or offer- curve is never inelastic in our sense of the term...." That, to me, qualifies Edgeworth as having introduced the term. Several subsequent authors also used the term, perhaps following Edgeworth or perhaps coming to it on their own. Some used it not to represent international trade, but rather for the supplies and demands of individual consumers. Bowley (1924) however was quite explicit, both in using the diagram which he said had been used "by many writers in the fundamental treatment of foreign trade" (p. 5), and in calling it the offer curve (p. 7). He cited Edgeworth's Mathematical Psychics from 1881 for the concept and mathematics of the equilibrium, but apparently not for the offer curve. The only other author who deserves mention here, however, is Lerner (1936). In this classic article on the symmetry between import and export taxes, his argument was built entirely on offer curves. In his opening sentence (p. 306) he stated as one of his purposes that he "demonstrates the applicability of Marshall's 'offer curve' apparatus to the elucidation of this problem." His use seemed to assume that readers were already familiar with both the diagram and the name for it, although his use of the quotation marks around it suggests that he didn't see the name as already universally adopted. But the use of the term in this still widely cited paper has surely secured its place in the lexicon of economics.
| |
| Ohlin definition | |
|
Relative factor abundance and scarcity can be defined either in terms of the relative quantities of factors -- the quantity definition -- or in terms of the relative prices of factors -- the price definition. In most renderings of the Heckscher-Ohlin Model, factor quantities are fixed but factor prices vary with trade, so if the price definition is used, it must be based on factor prices in autarky. The price definition is often attributed to Ohlin (1933) and thus is called the Ohlin definition. The quantity definition is less often given a name, although Bhagwati (1959) called it the Leontief definition, after Leontief1954.
Before Bhagwati (1959), however, Jones (1956) was the first to discuss these definitions extensively, and he repeatedly called the price version either "Ohlin's definition" or the "Ohlin definition." Therefore I attribute this term to Jones. Others, however, have not always called it the Ohlin definition, instead calling it the "Heckscher-Ohlin definition." In fact Jones himself, in his 1956 dissertation which included much of his 1956 article, in two places also called it the Heckscher-Ohlin definition. As for the quantity definition, Jones gave it no name, once simply calling it "mine." My search in Google Scholar found only eleven occurrences of "Ohlin definition," with or without "'s" or "Heckscher-", after Bhagwati (1959). Just four of these had "Heckscher-" preceding it. Of the remaining seven, the first three said "Ohlin's," while the last four said "Ohlin." Since 1975, the only term used has been "Ohlin definition," and these were by Helpman and Razin (1978), Maskus (1981), and Chipman (2006). It does appear that, while the terms no longer appear often in any form, "Ohlin definition" has become standard. This is not really fair to Heckscher, however, since it is clear that Ohlin adopted the price definition from his teacher, Heckscher. Heckscher (1919) included the following passage, which nicely summarized both the price definition and the Heckscher-Ohlin Theorem itself:
| |
| Optimal tariff | |
|
The terms optimal tariff and optimum tariff carry with them the implication that a positive tariff can be beneficial for a country from an overall economic welfare perspective. That is most often what their use today is meant to mean, rather than referring to the particular size of tariff that will achieve that optimum.
It was long recognized that a tariff, by improving the terms of trade, would provide a benefit that might possibly offset the loss that a tariff also causes by distorting markets. But Bickerdike (1906) was the first to show that this was not only possible but necessary, if there is any terms-of-trade effect at all and if the tariff is not too large. I've seen some also credit Edgeworth for this, as he addressed this topic in Edgeworth (1894). But as I read that, the result, if present, is hard to discern. And Bickerdike himself says that he is using the offer-curve and indifference-curve tools from Edgeworth (1894) to derive his own result, which he, and presumably his editor, regarded as new.
That there might exist an optimal (or optimum) level of such a tariff, once any benefit is known, follows immediately, since too large a tariff, such as a prohibitive one, must be harmful. But Kahn (1947) was the first to quantify what that optimal tariff might be. He expressed it in terms of elasticities of foreign supply of imports, η, and foreign demand for exports, ε:
In the same place, Johnson himself derived the following different, simpler, and equivalent formulae for "the optimum welfare tariff"":
If foreign demand is inelastic, as is quite possible and appears as a backward-bending foreign offer curve, foreign supply elasticity is negative and these formulae suggest a negative tariff. That is misleading, however, as the optimum would instead be a tariff large enough to move along the foreign offer curve to where demand is instead elastic. The message here is therefore not that one can determine the optimal tariff simply by measuring the foreign trade elasticity if that were possible, since that elasticity will likely change when the tariff is levied. The formulae only allow one to know, once a tariff is in place, whether it is optimal. Turning now to the origins of the terms optimal tariff and optimum tariff themselves, the first to come close to saying either was Kaldor (1940, p. 379) who spoke of the "optimal rate of import duty." He identified it in his diagram as that which achieves an offer-curve equilibrium at the tangency between the foreign offer curve and a trade indifference curve (without that name), but he did not attempt to quantify it.
It was Scitovszky (1942) who first used the term optimum tariff, as did both Kahn (1947) and Johnson (1951,1953/54) for their quantifications of it in terms of elasticities. Only in 1956 was Fleming (1956) the first use optimal tariff in print, in his title "The Optimal Tariff from an International Standpoint." It caught on, being used by many authors after that, although optimum tariff also continued to be used by many. Google's Ngram plot of the two terms shows that optimum tariff dominated optimal tariff until 1985, after which optimal tariff took the lead, and then use of both soon declined.
 My own view is that optimal tariff should be preferred, as "optimal" is clearly an adjective, while "optimum" is primarily a noun. | |
| Paradox of Plenty | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The phrase "paradox of plenty" has been used in other contexts since the 1930s, but it was introduced to the international economic context by Karl (1997), a few years after what has become the somewhat more common term meaning the same thing, resource curse.
I've found uses of paradox of plenty in multiple contexts over the years, ranging from "osteopetrosis and rickets" to pesticides. But the first uses of the term that I found were from, and about, the Great Depression. It first appeared in the title of a 1932 book by Harper Leech, The Paradox of Plenty, where it referred to the abundant potential availability of food and other things while the population was too poor to afford them. For several decades, most uses of the term referred to this and cited Leech. In 1993, the term was used again in the title of a book by Harvey Levenstein, Paradox of Plenty: A Social History of Eating in America. He too started with the Great Depression and the coexistence of soup kitchens and bread lines together with surpluses of milk, pigs, and grain. But he carried the term into the subsequent decades of actions by government and the private sector that expanded the availability of food while having questionable impact on nutrition. Karl, too, used the phrase in the title of her book, followed by the subtitle "Oil Booms and Petro States," making clear the difference from its uses by Leech and Levenstein. As she explained on page 242,
While Karl's book was not published until 1997, long after the dissertation, I found many citations of it including the term paradox of plenty before that, as early as 1994 listing it as "forthcoming" or "in press." And Karl herself used the term in other publications in 1990 and 1991. I would note that the main earlier uses of paradox of plenty associated plenty with poverty, but they did not -- as far as I know -- suggest that the plenty had caused the poverty. In contrast, as the above passage from Karl makes clear, her paradox of plenty does imply that resource abundance causes weak political systems to create disfunction and poverty. This is consistent with the message of the alternative term, resource curse that I define as equivalent to paradox of plenty. Karl (1982) did not use the term "resource curse," though she did on page 19 say "great wealth, it appeared, could be a curse as well as a blessing." Nor did Auty (1992), the coiner of resource curse, mention paradox of plenty, as far as I can tell from Google Books (I have not accessed the book itself). The two terms seem to have appeared independently. Perhaps not surprisingly, Google NGrams tells us that "resource curse" has been much more widely used than paradox of plenty, though the latter has continued to be used regularly: 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||