![Plant Operations Division [logo, Plant M]](../01-01_MLogo.gif)


Class project for ME599-Nano/Micro Structural Evolution, 2003 Winter, Advised by Professor Wei Lu
(4-1)
when and , Once a steplength is chosen, using the given initial value , the approximated value can be obtained. Therefore, the numerical solution can be described as follows
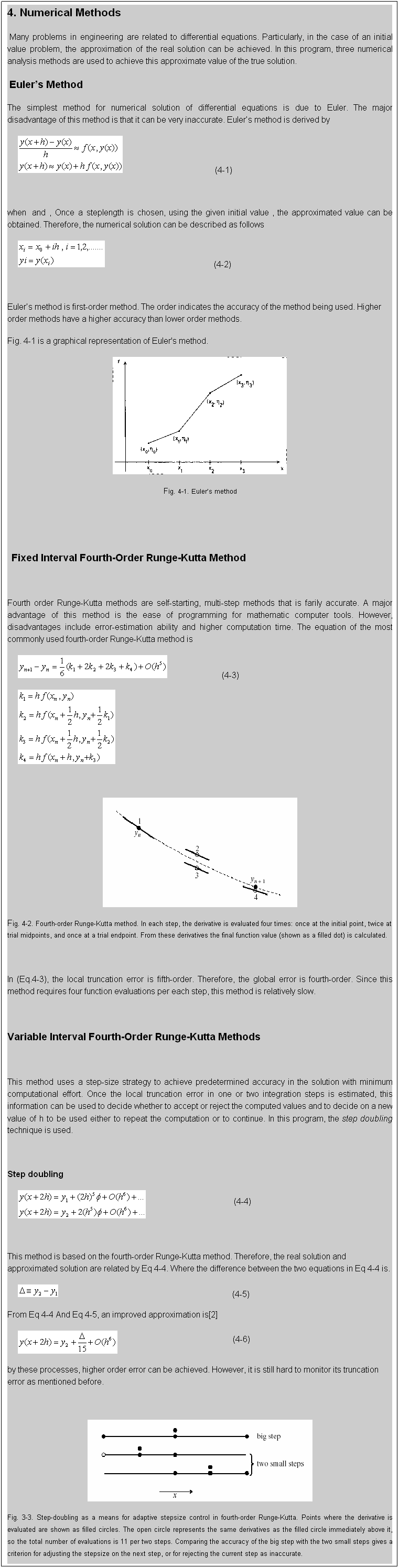
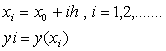 (4-2)
(4-2)
Eulerí»s method is first-order method. The order indicates the accuracy of the method being used. Higher order methods have a higher accuracy than lower order methods.
Fig. 4-1 is a graphical representation of Euler's method.
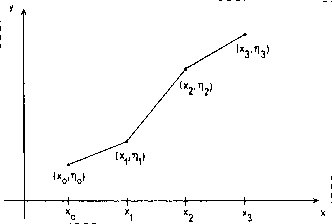
Fig. 4-1. Eulerí»s method
Fixed Interval Fourth-Order Runge-Kutta Method
Fourth order Runge-Kutta methods are self-starting, multi-step methods that is farily accurate. A major advantage of this method is the ease of programming for mathematic computer tools. However, disadvantages include error-estimation ability and higher computation time. The equation of the most commonly used fourth-order Runge-Kutta method is
![]() (4-3)
(4-3)
Fig. 4-2. Fourth-order Runge-Kutta method. In each step, the derivative is evaluated four times: once at the initial point, twice at trial midpoints, and once at a trial endpoint. From these derivatives the final function value (shown as a filled dot) is calculated.
In (Eq.4-3), the local truncation error is fifth-order. Therefore, the global error is fourth-order. Since this method requires four function evaluations per each step, this method is relatively slow.
Variable Interval Fourth-Order Runge-Kutta Methods
This method uses a step-size strategy to achieve predetermined accuracy in the solution with minimum computational effort. Once the local truncation error in one or two integration steps is estimated, this information can be used to decide whether to accept or reject the computed values and to decide on a new value of h to be used either to repeat the computation or to continue. In this program, the step doubling technique is used.
Step doubling
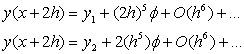 (4-4)
(4-4)
This method is based on the fourth-order Runge-Kutta method. Therefore, the real solution and approximated solution are related by Eq 4-4. Where the difference between the two equations in Eq 4-4 is.
![]() (4-5)
(4-5)
From Eq 4-4 And Eq 4-5, an improved approximation is[2]
![]() (4-6)
(4-6)
by these processes, higher order error can be achieved. However, it is still hard to monitor its truncation error as mentioned before.
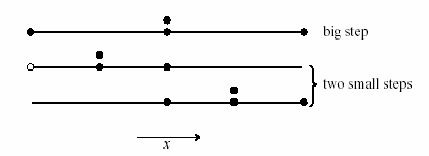
Fig. 3-3. Step-doubling as a means for adaptive stepsize control in fourth-order Runge-Kutta. Points where the derivative is evaluated are shown as filled circles. The open circle represents the same derivatives as the filled circle immediately above it, so the total number of evaluations is 11 per two steps. Comparing the accuracy of the big step with the two small steps gives a criterion for adjusting the stepsize on the next step, or for rejecting the current step as inaccurate.