Chapter
5
Binary Quadratic Forms
and the Löschian Diophantine Equation
One proof of Gauss's Law of Reciprocity, using
contemporary techniques was linked to at the end of the previous chapter.
There are also numerous classical proofs, some of which rest on the Chinese
Remainder Theorem (link
to one of them). Because such proofs often assume that the reader already
knows the Chinese Remainder Theorem, and because it has been our experience
that readers often do not know this theorem, we present it here in detail.
The
Chinese Remainder Theorem
At the time the greatest
common divisor was defined, it would have been possible to define a
related number, the least common multiple.
Definition
5.1. Suppose a and b are two positive integers.
The least common multiple [a, b] is the smallest positive
integer which is a multiple of both a and b. The relationship
between them is illustrated in the following lemma.
Lemma
5.2. Let a and b be two positive integers.
Then
a) (a, b)
[a, b] = ab
b) If d | a and d
| b, then d | (a, b)
c) If a | m and b
| m, then ab | m.
Proof:
a) Consider the prime factorizations
of a, b. Let
a = p1a1p2a2...pkak
b = p1b1p2b2...pkbk
(in this case, some exponents may be 0; a
prime is included in the list if it is a divisor of either a or
b).
Then
(a, b) = p1c1...pkck
where ci = min {ai, bi)
[a, b] = p1d1...pkdk
where di = max (ai, bi)
Since ai + bi=
ci
+ di for each i, (a,
b) [a,
b]
= ab.
b) There are integers s, t
such that (a, b) = as + bt. If a
= dx, b = dy, (a, b) = d(xs)
+ d(yt) = d(xs + yt). So d
| (a, b).
c) Let m = [a, b]q
+ r, 0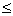 r<[a,
b].
As in b), since a | m and a | [a,
b], a
| r. Similarly b | r. Since r <
[a, b], this contradicts the fact that [a, b]
is the LEAST common multiple of a and b. So r
= 0. If (a, b) = 1, [a, b] = ab
by part a), so ab | m.
r<[a,
b].
As in b), since a | m and a | [a,
b], a
| r. Similarly b | r. Since r <
[a, b], this contradicts the fact that [a, b]
is the LEAST common multiple of a and b. So r
= 0. If (a, b) = 1, [a, b] = ab
by part a), so ab | m.
The least common multiple
is used in arithmetic to add fractions, where it is called the least common
denominator. For example, since [15, 21] = 15(21)/(15,21) = 15(21)/3
= 105
4/15 + 5/21
= (4/15)((21/3)/(21/3)) + (5/21)((21/3)/(21/3)) = (4(7) + 5(5))/105 = 53/105.
The least common multiple arises when it is
desired to solve several congruences (with different moduli) simultaneously.
The process below appears to have been known in first century China.
Hence it has come to be known as the Chinese Remainder Theorem.
Theorem
5.3. The Chinese Remainder Theorem
Let m1, m2,
..., mr be positive integers such that (mi,
mj)
= 1 if i j. Let a1,
..., ar be any integers. Then the system of congruences j. Let a1,
..., ar be any integers. Then the system of congruences
x a1
(mod m1) a1
(mod m1)
x a2
(mod m2) a2
(mod m2)
....
x ar
(mod mr) ar
(mod mr)
has a common solution of x, and
if x, y are two such solutions x y(mod
m=m1m2...mr). y(mod
m=m1m2...mr).
Proof:
For each j, let kj
= m / mj. Thus (kj, mj)
= 1, since mj has no factors in common with any mi
if i j. Thus there is
an integer bj with kjbj1 j. Thus there is
an integer bj with kjbj1 1(mod
mj).
Also, if i 1(mod
mj).
Also, if i j kjbj1 j kjbj1 0(mod
mi).
Let x = Skjbjaj
1 0(mod
mi).
Let x = Skjbjaj
1 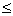 j
j 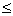 r. Then, for each
i,
x r. Then, for each
i,
x kibiai1 kibiai1 ai
(mod mi). Further, if x and y are
two solutions x ai
(mod mi). Further, if x and y are
two solutions x y(mod
mi).
Thus mi | (x - y) for each i.
By Lemma 5.2c) m | (x - y).
So x y(mod
mi).
Thus mi | (x - y) for each i.
By Lemma 5.2c) m | (x - y).
So x y(mod
m). y(mod
m).
Here is a classic
example. A man has a basket of eggs. He doesn't know how many
eggs there are, but when he counts them by twos, there is one left over.
Similarly, when he counts by threes or fives, there is one remaining.
When he counts by sevens, there are two left over. What is the least
number of eggs he could have in his basket? If x is the number
of eggs, the system of congruences is
x 1(mod
2) 1(mod
2)
x 1(mod
3) 1(mod
3)
x 1(mod
5) 1(mod
5)
x 2(mod
7) 2(mod
7)
So m=210,
k1=105,
k2=70,
k3=42,
k=30. To find b1,
b2,
b3,
b4 solve
105b11 1(mod
2) or b11 1(mod
2) or b11 1(mod
2) 1(mod
2)
70b21 1(mod
3) or b21 1(mod
3) or b21 1(mod
3) 1(mod
3)
42b31 1(mod
5) or 2b31 1(mod
5) or 2b31 1(mod
5) 1(mod
5)
30b41 1(mod
7) or 2b41 1(mod
7) or 2b41 1(mod
7) 1(mod
7)
One set of solution
is b1=1, b2=1, b3=3, b4=4.
Thus x=105(1)(1)+70(1)(1)+42(3)(1)+30(4)(1)=541. The smallest
positive integer congruent to 541(mod 210) is 121. Thus the least
number of eggs the man has is 121. |
While computations such as those of the
above example are fascinating, the theoretical consequences are more important.
Theorem
5.4. Suppose (m1,
m2)
= 1. Then the equation f(x) 0(mod
m=m1m2)
has a solution if and only if both f(x)
0(mod
m=m1m2)
has a solution if and only if both f(x) 0(mod
m1), and f(x)
0(mod
m1), and f(x) 0(mod
m2)
have solutions (here f(x) is a polynomial with integer coefficients).
0(mod
m2)
have solutions (here f(x) is a polynomial with integer coefficients).
Remark:
In fact if f(x) 0(mod
m1)
has n1 solutions and f(x)
0(mod
m1)
has n1 solutions and f(x) 0(mod
m2)
has n2 solutions, then f(x)
0(mod
m2)
has n2 solutions, then f(x) 0(mod
m)
has n1n2 solutions. See Niven,
Zuckerman, and Montgomery, Theorem 2.20, for a proof. In the
book, the theorem will be used to see if x21
0(mod
m)
has n1n2 solutions. See Niven,
Zuckerman, and Montgomery, Theorem 2.20, for a proof. In the
book, the theorem will be used to see if x21 a has solutions for certain composite moduli.
a has solutions for certain composite moduli.
Proof:
If f(x) 0(mod
m),
then for some integer k, f(x)
0(mod
m),
then for some integer k, f(x) km=km1m2.
Thus f(x)
km=km1m2.
Thus f(x) 0(mod
m1)
and f(x)
0(mod
m1)
and f(x) 0(mod
m2).
On the other hand, suppose f(x)
0(mod
m2).
On the other hand, suppose f(x) 0(mod
m1)
and f(x)
0(mod
m1)
and f(x) 0(mod
m2)
both have solutions. Suppose f(a1)
0(mod
m2)
both have solutions. Suppose f(a1) 0(mod
m1)
and f(a2)
0(mod
m1)
and f(a2) (mod
m2).
By the Chinese Remainder Theorem,
there is an integer x (mod m), x
(mod
m2).
By the Chinese Remainder Theorem,
there is an integer x (mod m), x a1(mod
m1)
and x
a1(mod
m1)
and x a2(mod
m2).
Then f(x)
a2(mod
m2).
Then f(x) f(a1)
f(a1) 0(mod
m1)
and f(x)
0(mod
m1)
and f(x) f(a2)
f(a2) 0(mod
m2).
Thus m1 | f(x),
m2 |
f(x).
Thus since (m1,
m2)
0(mod
m2).
Thus m1 | f(x),
m2 |
f(x).
Thus since (m1,
m2) 1,
by Lemma 5.2 m=m1m2 | f(x),
so f(x)
1,
by Lemma 5.2 m=m1m2 | f(x),
so f(x) 0(mod
m).
0(mod
m).
The Chinese
Remainder Theorem can also be used to help calculate the value of Euler's 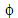 -function.
-function.
Theorem
5.5.
a) If p is a prime, 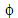 (pn)
= pn - pn-1
(pn)
= pn - pn-1
b) If (m1,
m2)
= 1, 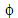 (m1,
m2)
=
(m1,
m2)
= 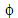 (m1)
(m1)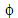 (m2).
(m2).
Proof:
a)
Suppose p is a prime. Then, consider the complete residue
system 1, 2, ..., pn. The only integers in this
list NOT relatively prime to p are p1, 2p,
..., (pn-1)p. Thus 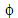 (pn)
= pn - pn-1.
(pn)
= pn - pn-1.
b) The goal
is to establish a one-to-one correspondence between integers a in
the set {1, 2, ..., m} which are relatively prime to m and
pairs of integers (a1, a2), where
a1
is in {1, 2, ..., m1}, relatively prime to m1
a2
is in {1, 2, ..., m2}, relatively prime to m2.
First, suppose (a,
m)
= 1. Then (a, m1) = 1 and (a,
m2)
= 1. Let ai be the remainder when a is divided
by mi, i = 1, 2. Second, suppose a1,
a2
are as above. Then the Chinese
Remainder Theorem assures there is a unique a in {1, 2, ...,
m}
with a a1(mod
m1)
and a
a1(mod
m1)
and a a2(mod
m2).
Since (a, m1) = 1 and (a, m2)
= 1, it follows that (a, m1m2)
= 1. Thus, since this one-to-one correspondence exists, f(m)
= f(m1) f(m2).
a2(mod
m2).
Since (a, m1) = 1 and (a, m2)
= 1, it follows that (a, m1m2)
= 1. Thus, since this one-to-one correspondence exists, f(m)
= f(m1) f(m2).
For example, since 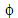 (4)
= 4 - 2 = 2 and
(4)
= 4 - 2 = 2 and 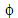 (5) = 4,
(5) = 4, 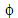 (20)
= 8. Since
(20)
= 8. Since 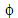 (8) = 8 -
4 = 4 and
(8) = 8 -
4 = 4 and 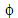 (9) = 9 - 3 = 6,
(9) = 9 - 3 = 6, 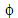 (72)
= 4(6) = 24. One of the pairings of part b) of the theorem is of
(1, 2), where (1, 8) = 1 and (2, 9) = 1 with 65, a number relatively prime
to 72 with 65
(72)
= 4(6) = 24. One of the pairings of part b) of the theorem is of
(1, 2), where (1, 8) = 1 and (2, 9) = 1 with 65, a number relatively prime
to 72 with 65 1(mod 8) and 65
1(mod 8) and 65 2(mod
9). This is the solution of the system
2(mod
9). This is the solution of the system
x 1(mod
8)
1(mod
8)
x 2(mod
9)
2(mod
9)
determined by the Chinese
Remainder Theorem (k1=9, k2=8;
b1=1,
b2=8)
since x 9(1)(1) + 8(8)(2)=137
9(1)(1) + 8(8)(2)=137 65(mod
72).
65(mod
72).
Binary
Quadratic Forms
In order to find
which integers are of the form
x2 + xy + y2
for
integers x,
y (as desired by Loeb
and Dacey), it is first necessary
to study binary quadratic forms in general.
Definition
5.6.
a)
A function f(x, y) = ax2 + bxy
+cy2 is called a binary quadratic form. If n
= f(x0, y0) for some integers
x0,
y0,
then the form f represents
n properly if (x0,
y0) = 1, improperly if (x0,
y0)  1.
1.
b) The points
(x, y) where x, y are integers are called lattice
points.
c) The discriminant
d
of a quadratic form is d = b2 - 4ac.
d) A form
is called
positive
definite if it takes on only positive values when (x, y)  (0,
0).
(0,
0).
negative definite
if it takes on only negative values when (x, y)  (0,
0).
(0,
0).
semidefinite if
it takes on only non-negative values or non-positive values.
Theorem
5.7.
a) d 0
or 1 (mod 4)
0
or 1 (mod 4)
b) A form
with d = 0 is semidefinite but not definite. A form with positive
discriminant is indefinite. A form with negative discriminant is
definite (positive if a>0, negative if a<0)
Theorem
5.8. Let
M = [m11m12;
m21,
m22].
Let [u; v] = M[x;
y], that is u
= m11x + m12y,
v
= m21x + m12y.
Then this transformation is a permutation of the lattice points in the
plane if and only if det M = +/- 1.
Definition
5.9. Two quadratic forms f(x,
y)
= ax2 + bxy + cy2 and
g(x,
y)
=
Ax2 + Bxy + Cy2 are said to
be equivalent if there is a matrix M of determinant 1, M
= [m11,
m12;
m21,
m22],
such that g(x,
y) = f(m11x
+ m12y,
m21x + m22y).
Theorem
5.8 suggests that matrices of determinant -1 could have been allowed
in Definition 5.9. Indeed, some number
theory texts allow this. Still others use the term "properly equivalent"
if det M = 1, "improperly equivalent" if det M = -1.
Niven, Zuckerman, and Montgomery use the approach of Definition
5.9.
Theorem
5.9.
a)
Equivalence of forms partitions the set of quadratic forms into sets of
forms all of which are equivalent to each other.
b) Equivalent
forms represent the same integers n, and represent the same integers
properly.
c) Equivalent
forms have the same discriminant.
Definition
5.10. Let f be a binary quadratic
form whose discriminant is not a perfect square; f is called reduced
if -|a| < b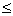 |a| < |c| or if 0
|a| < |c| or if 0 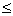 b
b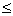 |a| = |c|.
|a| = |c|.
Theorem
5.11. If d is not a perfect square,
each equivalence class of binary quadratic forms of discriminant d
contains at least one reduced form.
Theorem
5.12. Suppose f is a reduced
positive definite quadratic form of discriminant
d. The 0
< a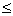 (-d/3)0.5
.
(-d/3)0.5
.
Corollary
5.13. There is only one reduced form
with discriminant -3.
Proof:
By Theorem 5.12 a = 1; b = 0 is impossible since d b2
(mod 4). Therefore, Definition 5.10 assures b = 1, c
= 1.
b2
(mod 4). Therefore, Definition 5.10 assures b = 1, c
= 1.
Theorem
5.14. Let n and d be given
integers with n 0. There
is a binary quadratic form of discriminant d which represents
n
properly if and only if x21
0. There
is a binary quadratic form of discriminant d which represents
n
properly if and only if x21 d(mod
4|n|) has a solution.
d(mod
4|n|) has a solution.
Corollary
5.15. Suppose d 0 or 1 (mod 4). If p is an odd prime, there is a binary quadratic
form of discriminant which represents p if and only if (d/p)
= 1.
0 or 1 (mod 4). If p is an odd prime, there is a binary quadratic
form of discriminant which represents p if and only if (d/p)
= 1.
Application
to Löschian Numbers
Definition
5.16. A positive integer n is called
Löschian
if there are integers x and y such that
n = x2
+ xy + y2.
Since there is only one reduced form of
discriminant -3, namely x2 + xy + y2,
and since if n is representable by a form of discriminant -3 if
and only if it is representable by an equivalent reduced form, Theorem
5.14 assures that n is properly representable by x2
+ xy + y2 if and only if x21 -3 (mod 4n) or x2 + 3
-3 (mod 4n) or x2 + 3  0(mod 4n) has a solution.
0(mod 4n) has a solution.
By Theorem 5.4,
x2
+3  0 (mod 4n)
has a solution if and only if x2 +3
0 (mod 4n)
has a solution if and only if x2 +3  0 (mod piai) has a solution for every i.
0 (mod piai) has a solution for every i.
1) If p | n
and p 1 (mod 3), then
by quadratic
reciprocity (-3/p) = (p/3) = 1 and also (-3/pn)
= (pn/3) = (p/3)n = 1, so x2
+3
1 (mod 3), then
by quadratic
reciprocity (-3/p) = (p/3) = 1 and also (-3/pn)
= (pn/3) = (p/3)n = 1, so x2
+3  0(mod pn)
has a solution for every n.
0(mod pn)
has a solution for every n.
2) However suppose p 2(mod
3). Then (-3/p) = 1, and so x2 +3
2(mod
3). Then (-3/p) = 1, and so x2 +3  0(mod p) has no solution. But x2 +3
0(mod p) has no solution. But x2 +3 0(mod
pn)
implies pn | (x2 +3) which in turn
implies that p | (x2 +3), which is impossible.
0(mod
pn)
implies pn | (x2 +3) which in turn
implies that p | (x2 +3), which is impossible.
3) Of course x2
+3 0(mod 3) has a solution (x
= 0) but x2 +3
0(mod 3) has a solution (x
= 0) but x2 +3 0(mod
3n) has no solution for n>1 since 9|(x2
+3) implies 3|x2 implies 3|x, say x=3a;
but then x2 +3 = 3(3a2 + 1)
0(mod
3n) has no solution for n>1 since 9|(x2
+3) implies 3|x2 implies 3|x, say x=3a;
but then x2 +3 = 3(3a2 + 1) 3
(mod 9), a contradiction.
3
(mod 9), a contradiction.
Thus N is properly representable by
x2
+ xy + y2 if and only if
N = 3appb,
where every p 1(mod 3)
and a =0 or 1. Of course if N =
x2 +
xy
+ y2 , c2N = (cx)2
+ (cx)(cy) + (cy)2 so the square of any
properly representable integer is improperly representable. Thus
an integer N is Löschian if and only if N = 3appbpq2g
where every p
1(mod 3)
and a =0 or 1. Of course if N =
x2 +
xy
+ y2 , c2N = (cx)2
+ (cx)(cy) + (cy)2 so the square of any
properly representable integer is improperly representable. Thus
an integer N is Löschian if and only if N = 3appbpq2g
where every p 1(mod 3),
every q
1(mod 3),
every q 2(mod 3).
Of course, sometimes, it is not necessary to find the prime factorization
of N to see if it is Löschian. Since always x2
+ xy + y21
2(mod 3).
Of course, sometimes, it is not necessary to find the prime factorization
of N to see if it is Löschian. Since always x2
+ xy + y21 0 or 1 (mod 3) [try the nine cases x
0 or 1 (mod 3) [try the nine cases x a,
y
a,
y b
(mod 3); if a = b, x2 + xy +
y21
b
(mod 3); if a = b, x2 + xy +
y21 0(mod 3); otherwise x2 + xy + y21
0(mod 3); otherwise x2 + xy + y21 1(mod 3) ].
1(mod 3) ].
So if N 2(mod
3),
N is non-Löschian.
2(mod
3),
N is non-Löschian.
For example, N=32759
is non-Löschian (it is not immediately obvious that N = 17(41)(47).
Similarly, suppose N = pnM,
where (M,
p) = 1, p 0,
1 (mod p). If M
0,
1 (mod p). If M 2(mod
3), N is non-Löschian, since the sum of the exponents of the
primes
2(mod
3), N is non-Löschian, since the sum of the exponents of the
primes  2(mod 3) in the
prime factorization of M must be odd.
2(mod 3) in the
prime factorization of M must be odd.
For example, N
= 8073 = 33(299), and 299  2
(mod 3). So 8073 is non-Löschian. In fact, 8073 = 33(13)(23).
2
(mod 3). So 8073 is non-Löschian. In fact, 8073 = 33(13)(23).
In summary,
Theorem
5.17. Let N be a positive integer. Then
a) N is properly
representable as x2 + xy + y2
for integers x, y if and only if N = 3aM,
where a = 0,1 and every prime factor of M is  1(mod 3).
1(mod 3).
b) N is Löschian if
N
= 3aMT2, where every prime factor of M
is  1(mod 3) and every
prime factor of T is
1(mod 3) and every
prime factor of T is  2(mod 3).
2(mod 3).
c) N is non-Löschian
if N 2(mod 3)
2(mod 3)
d) N is non-Löschian
if N = pnM, (M, p) = 1, M 2(mod
3).
2(mod
3).
Löschian numbers:
examples of Theorem usage
In this chapter,
we have proved a theorem that lets anyone determine exactly which numbers
are Löschian and which numbers are not Löschian. The formal
mechanics of proof drew on a variety of earlier theorems and on facts from
number theory. The creative effort involved the recasting of Marshall's
earlier work in a form that would lead to the desired conclusion of a sufficient
condition. Readers wishing to examine the history of this development
are referred to articles published by Marshall
(1975), S. Arlinghaus (1985), and
S.
Arlinghaus and W. Arlinghaus (1989). So that one might see how
the results of Theorem 5.17 can be implemented, we offer several examples
below.
-
K = 175 is Löschian, since
K
= 52 x 7.
-
K = 125 = 53 is not Löschian
-
K = 245 = 5 x 72 is not Löschian
-
K = 85 is not Löschian, even though
85 is congruent to 1(mod 3), since K = 5 x 17, and both 5 and 17
are congruent to 2(mod 3)
-
K = 49 is Löschian as 49 may be
generated using the Diophantine equation on either the ordered pair (0,
7) or on (3, 5): representation is not unique.
Theorem 5.17 offers an easy way to check whether
a given number is Löschian. It does not give the geometric characterization
of the associated hierarchy. For that characterization, the reader
then needs to return to the material in Chapter 4 and the Fundamental
Theorem offered there.
Institute
of Mathematical Geography. Copyright, 2005, held by authors.
Spatial Synthesis:
Centrality and Hierarchy, Volume I, Book 1.
Sandra Lach Arlinghaus and
William Charles Arlinghaus
![]() r<[a,
b].
As in b), since a | m and a | [a,
b], a
| r. Similarly b | r. Since r <
[a, b], this contradicts the fact that [a, b]
is the LEAST common multiple of a and b. So r
= 0. If (a, b) = 1, [a, b] = ab
by part a), so ab | m.
r<[a,
b].
As in b), since a | m and a | [a,
b], a
| r. Similarly b | r. Since r <
[a, b], this contradicts the fact that [a, b]
is the LEAST common multiple of a and b. So r
= 0. If (a, b) = 1, [a, b] = ab
by part a), so ab | m.