Cohort-Survival Analysis

600 people live in the mysterious country of Pangaea. The country is not found on any map, nor is it visited by ships or aircraft; as a result, there has been no migration to or from the country. Use cohort-survival analysis to answer the following two questions.

1. SCENARIO ONE: Project the total population, and the number of people in each 10-year cohort, for the years 2010 and 2040 [the blue-shaded cells in the table below]. Show your work. [closed population scenario - population changes due only to natural increase/decrease  download this table in Excel format

ANSWER

Cohort Survival Analysis -- to forecast population in the future

Note: the method below comes up with a HIGH ESTIMATE -- all those who enter a cohort are at risk of having a child.

Age Group (years)	Population in Year 2000	Survival Rate	Birth Rate	Population in Year 2010	2020	2030	Population in Year 2040
0 - 9	100	0.95	0	131	134	140	160
10 - 19	100	0.99	0.3	95	124	127	133
20 - 29	100	0.95	0.7	99	94	123	126
30 - 39	80	0.92	0.3	95	94	89	117
40 - 49	70	0.9	0.1	74	87	87	82
50 - 59	50	0.8	0	63	66	79	78
60 - 69	40	0.7	0	40	50	53	63
70 - 79	30	0.5	0	28	28	35	37
80 - 89	20	0.3	0	15	14	14	18
90 and above	10	0.1	0	7	5	5	5
TOTAL	600			646.6	697.5	751.8	818.1
rounded				647	697	752	818

Notes:
survival rate -- proportion of people in cohort who survive into next cohort.
birth rate -- the number of children born per person in cohort during the time interval (ten years)
Population for a given year is counted on January 1 (e.g., on January 1, 2000 the population was 600 people).

Comments:

1. Don't forget to include the ten percent of people who are already in the open cohort (90 years and older) who survive. These people survive into the same cohort (e.g., to estimate the 2010 population of the 90+ cohort: 20 * .3 + 10 * .1 = 7).
2. A common mistake is to have people give birth to children who are the same age as their parents! (e.g., births from the 20-29 year-old cohort erroneously get added to the 20-29 year-old cohort). The correct method: enter all of these births into the 0-9 cohort. For example: to estimate the 2010 population of the 0-9 cohort: 100 * 0.3 + 100 * 0.7 + 80 * 0.3 + 70 * 0.1 = 131.
3. There are several strategies for rounding numbers in your calculations. You can leave your numbers for cohort sizes in fractions, or you can round at each step. For this assignment, either approach is fine (but do note if you use a rounding strategy).

Alternative Estimates:

One important question (regarding how one calculates the numbers of births) is determining who is "at risk" of leading to a birth. Here there are three alternatives: (a) assume that anyone who enters a cohort (regardless of whether they die during that cohort period) is "at risk" (this is the assumption used in the in-class handwritten example, which will lead to a slight overestimate of children born); (b) assume that only those who survive the entire cohort period is "at risk" (which will lead to a slight underestimate of children born); or (c) use an average of the two (which would lead to a middle estimate). For this assignment, any of the three approaches is fine. Please do note what assumptions you make.

Low estimate: If you made the assumption that only those who survive through the entire 10 year cohort period are "at risk" of having a baby, then the estimate would be lower: 640 people in the year 2010, and 784 people in the year 2040.

Middle estimate: If you compromised and assumed that those people alive at the middle of the cohort are at risk of having a baby -- assuming linear rates of mortality within the cohort -- then the resulting values are 643 people in the year 2010, and 801 people in the year 2040.)

2. SCENARIO TWO (open population with migration): Pangaea is worried about insufficient population growth, and decides to use in-migration (rather than encouraging increased fertility) to stimulate faster population growth. The country decides to invite 50 outsiders to move to the island on January 2, 2000. To maximize the country's population in time for the nation's Centennial in the year 2040, what age group(s) should the 50 immigrants belong to in 2000? What would the total population and population by age group be in 2040? [the blue-shaded cells in the table below]

50 migrants in the age 10-19 cohort would maximize the population in the year 2040. New migrants potentially contribute to population increases in two ways: (a) they increase the population themselves (and this has a longer impact if they have a longer life expectancy from the age of migration), and (b) they give birth to new residents. Migrants aged 10-19 cohort do both, and they experience all their reproductive years in Pangaea, while still having a long life expectancy (so that most will still be around in the year 2040). (Note: migrants in the age 20-29 cohort would lead to the second-highest population increase. Migrants in the 0-9 age category would contribute the most person-years to the island population, but since they would not begin reproducing for another 10 years, their impact on the next generation is less rapid. Migrants in the 50+ year age categories would have no long-term impact on population levels.)

Two important notes:

1. the assignment specified that the 50 migrants arrive on January 2, 2000 (therefore at the BEGINNING of the first ten-year time period). As a result, they are "at risk" of giving birth to new Pangaeans during the entire 2000 - 2010 decade. (If you mistakenly added them at the end of the decade rather than at the beginning, your population estimates will be too low.)

2. It is important to explain and demonstrate HOW you determined that the 10-19 cohort is the right answer: (a) trial and error? (b) a good guess? (c) logical deduction? In this case, you can logically eliminate from the outset all cohorts past the reproductive years (i.e.,50+ years old) [strategy (c)], but you likely need to actually run the numbers on the other scenarios to see which has the highest population outcome [strategy (a)].

Comparison of future population levels based on different migrant age group scenarios:

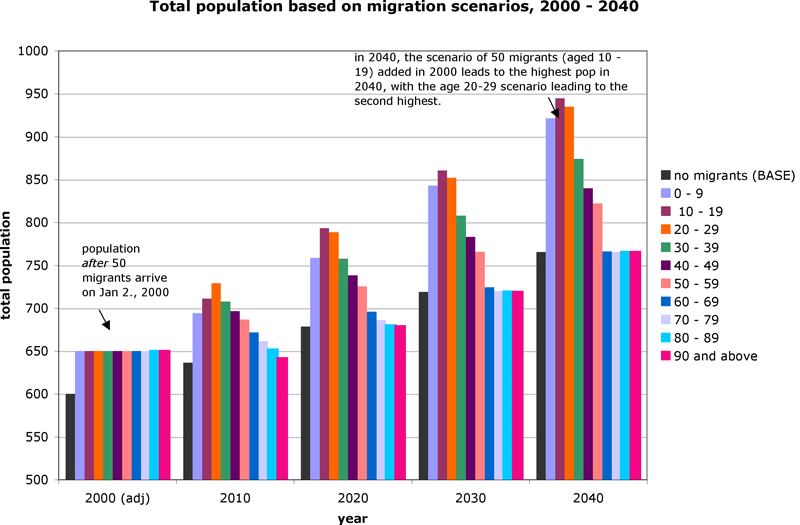
Note that migrants in the older age groups have little or no impact on long-term population levels: few survive to the year 2040, and they migrate to Pangaea after they have aged-out of their reproductive years.

3. Optional Extra credit: estimate the life expectancy (e₀) of a Pangaean baby born in the year 2000. (Briefly explain and document your method.)

ANSWER

The life expectancy (e₀) is 63.6 years, which is e₀ = T₀ / l₀ = 6127.4 / 100 = 61.3.

Age Group (years)	Survival Rate [GIVEN]	qx (proportion dying = 1-survival rate)	lx (number living at beginning of age interval)	Lx (Stationary population in the age interval)	Tx (stationary population in this and all subsequent age intervals -- that is, cumulative Lx)	ex (life expectancy at beginning of age interval, in years)
0 - 9	0.95	0.05	100.0	975.0	6127.4	61.3
10 - 19	0.99	0.01	95.0	945.3	5152.4	54.2
20 - 29	0.95	0.05	94.1	917.0	4207.1	44.7
30 - 39	0.92	0.08	89.3	857.7	3290.2	36.8
40 - 49	0.9	0.1	82.2	780.9	2432.4	29.6
50 - 59	0.8	0.2	74.0	665.8	1651.5	22.3
60 - 69	0.7	0.3	59.2	503.1	985.7	16.7
70 - 79	0.5	0.5	41.4	310.7	482.6	11.7
80 - 89	0.3	0.7	20.7	137.8	171.9	8.3
90 and above	0.1	0.9	6.8	34.2	34.2	5.0

1. Life expectancy is simply the average number of person-years lived = total person-years lived (T₀ = sum of all L_x) divided by the number of persons (l_x).
2. Remember that calculating life expectancy is independent of both birth rates and the existing structure of the population (here, the allocation of the country's 600 residents by age group in the year 2000). In other words, the life expectancy of a baby at birth is NOT calculated based on either birth rates or the age structure of the existing population.
3. To calculate life expectancies, you only need mortality rates (which is q _x = 1 - survival rates). Knowing q _x, you can then also calculate l _x, L _x, T₀, and then finally e_{0 =} T₀ / l₀.
4. To get the values of l_x, simply pick a hypothetical number for l₀ and then use q _x to calculate the subsequent values for l_x (e.g., l₁₀, l₂₀, etc.). Do NOT use the existing age structure from the first part of the assignment -- that is irrelevant for estimating life expectancies.
5. Demographers usually estimate L _x differently for the youngest and oldest age cohorts as compared to the other cohorts (where we can assume that L _x = n * (l _x + l _x+1 )/2. However, to keep this assignment simple, you may use the same assumption for these two cohorts (here, L ₀ and L ₉₀ ). Remember that l _infinity = 0 (i.e., everyone eventually dies).
6. Since the cohort sizes are n = 10 years (rather than n = 1 year), be sure to adjust your L _x to reflect this 10 year interval -- i.e., multiply by 10 years -- otherwise you may get a life expectancy estimation of 6.13 years, which is a short life!.

Further comments / advice:

Cohort -Survival Method

1. Using matrix algebra is a mathematically powerful way to perform cohort survival analysis (e.g., P ₁ = C * P ₀ , or more generally, P _n = C ⁿ * P ₀ , where P _n is the age-specific population array for time period n and C is the components of change matrix, which includes both age-specific birth rates and survival rates). However, you do NOT need to answer this question using matrices. Instead, simply using Excel calculations may be an easier way to proceed.