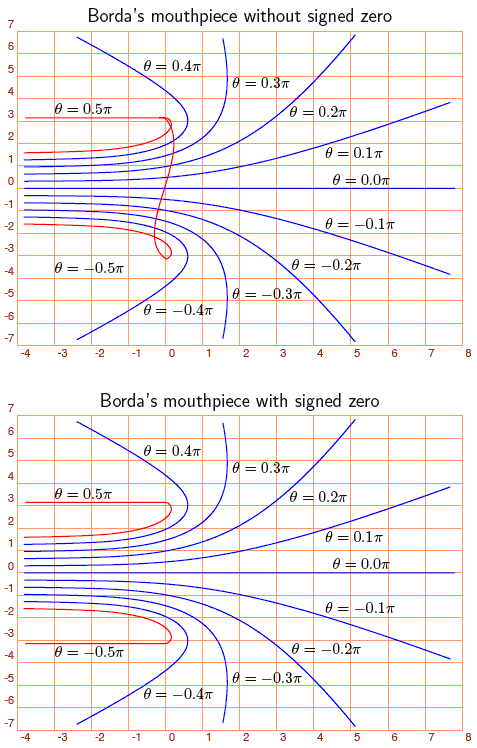
The above plots replicate William Kahan's dramatic example of the difference between the proper and improper use (or nonuse) of signed zero on branch cuts. See his article on The Baleful Effect of Computer Benchmarks for the original plots. That article was incorporated into his 1997 S.I.A.M., John von Neumann lecture.

The contours in the plots are images F(z) of rays z = r e^iθ at constant θ, where

using principal branch definitions of the complex square root and natural logarithm. The red contours have parts that are right on the branch cuts, which causes trouble when signed zero is not treated correctly.

The lower, correct plot uses Kahan's algorithms for treating IEEE 754 signed zero in the square root and logarithm, implemented in our revisions of Julian Noble's ANSForth complex arithmetic lexicon. The ANSForth implementations in complex.fs and complex-kahan.fs, as well as the primitive code in pfe's COMPLEX-EXT environment, give indistinguishable results for these plots, done in double precision on a PowerMac G4 under MacOS 10.3.3.

The upper, incorrect plot is from Fortran, compiled with g77, gcc version 3.4 20031015 (experimental), run under the same Macintosh system. It is like Kahan's plot without signed zero, except that the plotting software we use interpolates a curve between the points on the θ = -π/2 contour where the imaginary part develops a (spurious) jump between -π and π, whereas his interpolates a straight line.

The source files for the calculations and for a pdf version of this document are available under Borda's mouthpiece at the following url:

David N. Williams
February 5, 2005