Live video of battery tester

Motivation: Plug-in hybrid electric vehicles (PHEVs) have two or more energy sources, most typically an internal combustion engine and high-energy capacity battery. Ideally, one would like to efficiently utilize both depletable energy sources in an optimal manner, for a stochastic distribution of driving behaviors.

Research Question: How does one optimally blend engine and battery power in a PHEV to minimize energy consumption cost and battery health degradation?

Approach:

• Define objective to include the costs of fuel and electricity replenishment when plugged into the grid.
• Include reduced-form versions of models for electrochemical capacity fade mechanisms
• Model drive cycle dynamics as a Markov chain, with a terminal state representing the "vehicle off" state, which integrates a sense of trip length distributions.
• Formulate a multi-objective constrainted dynamic optimization problem
• Apply stochastic dynamic programming tools

Key Results:

• Optimal blending can provide significant economic benefits to owners, particularly for certain fuel-to-electricity price ratios.
• Daily trip length, that is the distance travelled between recharging events, plays a significant role in how aggressive one depletes battery state-of-charge.
• There exists a fundamental tradeoff between energy consumption cost minimization and battery health enhancement.
• Battery state-of-charge management for battery health is strongly related to the monotonicity properties of the battery health degradation mechanism.

Motivation: Recent advances in lihtium-ion battery modeling suggest health may be improved by allowing unequal yet controlled charge levels in battery packs.

Research Question: How does one optimally management charge levels in battery packs to enhance battery life?

Approach:

• Develop advanced models of battery charging and capacity fade dynamics, namely anode-side SEI film growth.
• Propose a battery pack topology which uses controllable relay switches to enable unequal charge levels
• Include reduced-form versions of these models for control optimization.
• Formulate a constrainted dynamic optimization problem and solve using deterministic dynamic programming principles.
• Validate the optimal charging trajectories on high fidelity simulation models.

Key Results:

• Optimal equalization or unequalization is directly related to the convexity properties of the degradation mechanisms.
• From this insight, approximatly-optimal static state-feedback controllers can be synthesize
• These implementable approximate controllers provide significant reduction in anode-side film growth.

Motivation: A broad spectrum of physical engineering systems exhibit diffusion-reaction dynamics, e.g. structural acoustics, fixed-bed reactors, multi-agent coordination control, and stock investment models. A subset of these systems limit control and sensing to the boundaries, such as thermal/fluid flows, cardiovascular systems, chemical reactors, and advanced batteries. Optimal control and estimation of these PDE systems is particularly challenging since actuation and sensing are limited to the boundary and the dynamics are notably more complex than ODE systems. Motivated by this fact, this thrust area's overall goal is to develop optimal boundary control and estimation algorithms for parabolic PDE systems.

Research Question: How do we extend optimal control and estimation theory of finite-dimensional systems to infinite-dimensional systems with actuation and sensing at the boundaries only?

Approach:

• Formulate a linear quadratic optimal control/estimation problem.
• Apply concept of weak-variations to derive the necessary conditions for optimality.
• Derive the conditions for a time-varying state feedback, which forms a Riccati-type PDE.
• Analyze and compare method to existing control techniques for PDEs.
• Experimental application studies

Key Results:

• A constructive method for deriving optimal boundary control and estimation results for PDE systems.
• Necessary conditions for optimality, which manifest themselves as coupled PDEs with split initial/final conditions.
• Riccati-type PDEs whose solutions are related to the optimal state-feedback and observer gains.

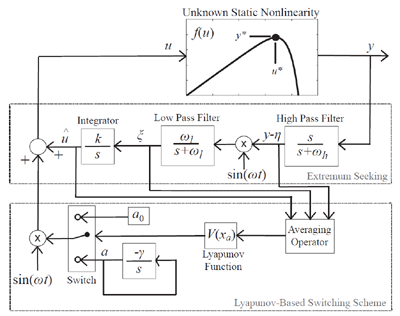Motivation: Extremum seeking deals with the problem of regulating a system to an unknown optimal set-point, which may be time-varying. Once this optimal setpoint is identified most algorithms converge to a limit cycle about this point, rather than converging to it exactly. This can have significant implications on, for example, the power conversion efficiency of photovoltaic (PV) systems.

Research Question: How does one design an extremum seeking algorithm which converges to the optimal operating point in the exact sense?

Approach:

• Begin with the design for standard extremum seeking systems.
• Use the analysis methods in the stability proofs to pose a Lyapunov function which represents proximity to the optimal operating point.
• Calculate the Lyapunov function online and when its value falls below a threshold, then allow the perturbation signal to decay exponentially.
• Apply and test the proposed Lyapunov-based extremum seeking method to the maximum power point tracking problem in photovoltaic systems.

Key Results:

• Indeed, the Lyapunov-based extremum seeking method converges to the exact optimal operating point, even in the presence of noise.
• A Lyapunov-based approach exhibits desirable properties. For example, the level sets are invariant with respect to the system dynamics, therefore eliminating the chance for chattering at the switching threshold.
• The algorithm is self-optimizing in the presence of perturbations, such as temperature and solar irradiation shifts in PV systems.
• Validation against traditional maximum power point tracking algorithms in simulation and experiments show significant improvements in conversion efficiency.