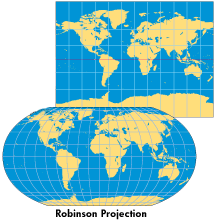
| The only true representation of the earth, free
of distortion, is a globe. Maps are flat, and the process by which geographic
locations (latitude and longitude) are transformed from a three-dimensional
sphere to a two-dimensional flat map is called a projection.
Every map projection distorts at least three, and sometimes all four, of the following properties: Shape, Area, Distance, and Direction. Conformal: No map can preserve the shape of large areas, but a conformal projection maintains shape in small, localized areas. Equal Area: These projections show the areas of all regions on the map in the same proportion to their true areas on the globe. Equidistant: No map can show distance correctly between all points on the map, but only from one, or at most two, points to any other point. Azimuthal: This projection correctly shows directions (azimuths) from a single point to all other points on the map. |
To better understand what happens
during the projection process, imagine the earth as a large inflated balloon.
 |
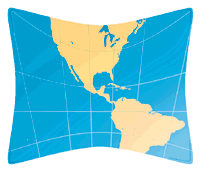
Cut it apart, and flatten it to make
a map. It will be stretched in some places, shrunk in others. Think of
where and how the original balloon has been distorted.
 |
|
|
|
One method of classifying map projections is to group them by the type of surface onto which the graticule is theoretically being projected: Cylindrical, Conic, and Azimuthal. Map projections that do not fit within these three classes are described as Pseudo or Miscellaneous projections. Though few maps are truly the result of such projection (most are derived from mathematical formulas), it is a useful way to visualize and understand the transformation process. Where the projection surface touches (is tangent to) the globe, scale is true. This can be at a point, or along one or two lines (called standard lines, or, if along a line of latitude, standard parallels). Distortion increases with increasing distance from the standard point or lines. |
| CYLINDRICAL
Imagine a light bulb in the center of a globe, with a sheet of paper wrapped around it in the form of a cylinder. Meridians and parallels would be "projected'' onto the cylinder as straight, parallel lines. Because meridians on these projections do not meet at the poles, as they do on the globe, these maps are increasingly stretched and distorted toward the poles. Pseudocylindrical projections normally have straight parallels and curved meridians (usually equally spaced). The Robinson Projection is a popular example. It was created to make the world "look" right by keeping angular and areal distortions to a minimum. |

|
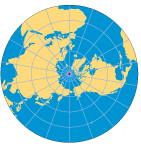
| AZIMUTHAL
A perfectly flat piece of paper (a plane) would touch the globe at a point. This projection is a good choice for maps with circular or square shapes. When the point of tangency is one of the poles, meridians are shown as straight lines radiating from the pole. If parallels are then drawn as equally spaced concentric circles, this projection would be equidistant (scale is true along any line radiating from the center point, in this case the pole). Gnomonic Projection: Great circle routes (the shortest distance between two points on the globe) appear as straight lines on this Azimuthal |
|
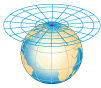
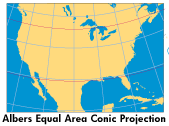
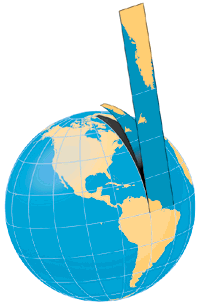
| CONIC
A cone of paper placed over a globe would touch its surface along one standard line (usually a parallel). A cone that sliced through the globe would intersect it twice, creating two standard parallels. Such a projection is well-suited for showing areas in the middle-latitudes with a mostly east-west extent (like the United States). |
 |
 Visualize the properties of a map projection by comparing the arrangement
of its meridians and parallels with the characteristics of the graticule
on the globe: Parallels are spaced equal distances apart.
Visualize the properties of a map projection by comparing the arrangement
of its meridians and parallels with the characteristics of the graticule
on the globe: Parallels are spaced equal distances apart.