UP 507

Final Project

The goal of this project is to integrate the conceptual principles taught over the course of the semester with the GIS technical skills that we have been exposed to in this class.

Where? The Fiji Islands

Background 

The social organizations on the Fiji islands have been described as chiefly organized. What this means is that the socio-political complexity found on these islands at the time of European contact falls in the “"socio-evolutionary scale of development" in the intermediary stage between tribal society and state level organization (Service, 1962)

Chiefdom population sizes range from "low thousands to tens of thousands”" (Johnson, 1987), and are socially organized into hierarchies, where at a local level an individual's relationships to the apical leader can be mapped in the local social cosmology. Thus, an individual's potential to rule over others is determined relationally, whereby one's proximity along kinship lines to a founding ancestor or supernatural force is not only measurable, but up for social comparison and competition.

At the regional scale, the paramount chief is the highest-ranking elite in the highest-ranking lineage and has the authority to manipulate the flow of trade between local chiefdoms, and to dictate social taboos that restrict access to specific goods and resources. As chiefdoms develop more complex forms of authority and organization, the direction of accessible goods and resources departs from models that predict least-cost pathways between different productive nodes in an island network.

For this project, I will assume a reduced model of interactive complexity between nodes, and will only attempt to understand island trade and exchange with a simple set of parameters.

This analysis relies on two previous studies in the literature. First is the use of graph theory and network analysis by Hage and Harary in Island Networks (1996), where the authors applied sophisticated mathematical concepts to understanding "a variety of social, cultural, and linguistic relations" in Polynesian Islands. Graph theory is useful for our analysis, because its application defines elements by their relational position with other elements in the overall structure. The position and relationship of the elements (a finite set of V nodes) is defined by a set of E edges. The graph theoretic model that we will be using is a simple TREE diagram. This is useful because graph models are not bound to fixed coordinate systems, which would otherwise assign each node (V) a known X-Y-Z position, and each vector (E) a value corresponding to a three dimensional direction and magnitude. Therefore, graph models exist abstracted from fixed interpretive frames. This makes each model autonomous, defined and interpretable by its own properties, and free from the distortions that are incurred in the radical translation of spatial data between coordinate systems that rely on a different set of logical assumptions and truths about the frame universe (Quine, 1969 )--(As an example, consider the reprojection of maps between different systems that assume different datums and representations of the earth's shape).

A second piece of work that is important for this paper is the simulation carried out by Wright and Zeder (1977), where a node system exchange network was developed to test the stability of exchange systems under three conditions. The goal of the project was to see whether a network of linearly arranged nodes (arranged in a chain, not a web), that engaged in artifact trade, would achieve equilibrium as a system or whether the system maintained itself in constant flux stimulated by the unidirectional flow of either 1) vital goods, 2) symbolic goods 3), or a combination of both. System stability was interpreted as the decline of flow of goods, and was considered unsuccessful in terms of understanding the regional integration of various production and distributional sites. An unstable system demonstrated that the circulation of goods was continued, and this was only achieved when the flow of goods was composed of vital and stable goods, and there were multiple distribution centers.

What the Java Applets will provide for Fiji, is to see whether a hypothetical system of trade between nodes will achieve stability or not, and to understand under what conditions either of this outcomes will occur.

Steps

	Registration of Fiji map, and the creation of a line and point shape file.
	Island buffering to determine node count based on a spatial hierarchy relationship.

Node Counts based on arbitrary distance on control

A networked system with a highly centralized distribution center that integrates all of the islands.

Click here

A networked system that only assumes one relationship per node. The relationships is defined by closeness in space.

Click here

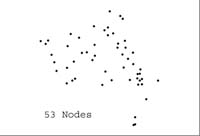	O Km Buffer
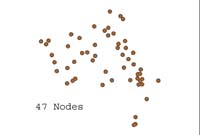	10 Km Buffer
	20 Km Buffer
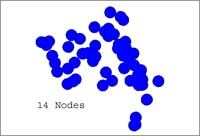	30 Km Buffer

References Cited

Johnson, A. and T. Earle (1987). The Evolution of Human Societies. Stanford, Stanford University Press.

Quine, W. V. O. (1969). Ontological Relativity, and other essays, by W. V. Quine. New York, Columbia University Press.

Service, E. (1962). Primitive Social Organization. New York, Random House.

Wright, H. and M. Zeder (1977). The simulation of a linear exchange system under equilibrium conditions, In T.K. Earle and J.E. Ericsson (eds.), Exchange systems in Prehistory, New York: Academic Press, pp. 233-253