*note: the group is abelian if it also is commutative, ab=ba, but not all groups satisfy this property.
Subgroup: a subset, H, of the original group satisfying the group conditions
under the operation of the original group, G.
Proper subgroup: if H is a subgroup of G,
but does not equal G, totally contained within the group.
Trivial subgroup: the identity alone.
Nontrivial subgroup: any subgroup that is
not the identity.
Order of a Group: the number of elements the group contains.
Order of an Element: the smallest positive integer n such that g^n=e, g is the element.
The abstract approach to determining if a set is a group is that the set has only one identity element, the right and left cancellation laws hold, ba=ca implies b=c, and ab=ac implies b=c, and the inverses are unique. Since I was hopefully going to relate these mathematical concepts to skiing, Sandi and I decided to work with the symmetries of a square to explain the mathematical concepts in hopes that it could then be related to the various snow colors of the slopes. The symmetry group of a plane figure includes the set of all symmetries of the figure, which are rotations and reflections. First one must imagine a square with the four corners numbered from 1 to 4.

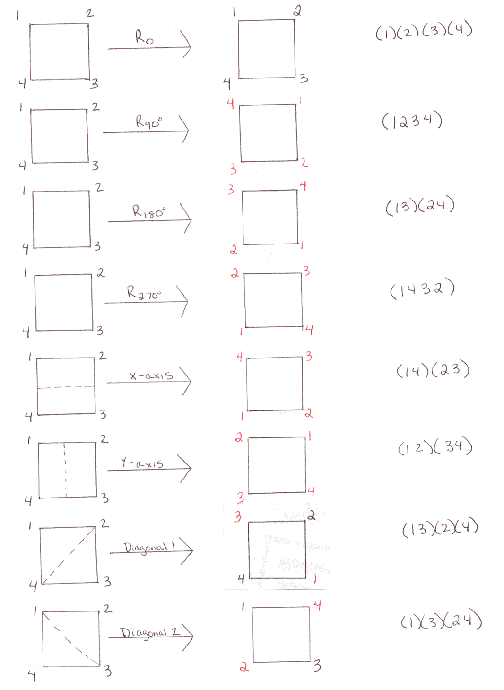
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Within this group there is
the possibility that there are subgroups. Using the definition from
above, I was able to find eight subgroups and the identity. Five
are of the order 2 and three are of the order 4 because of how many elements
are in the subgroup. I=(1)(2)(3)(4) which is the trivial subgroup
Order 2: (12)(34), I
(13)(24), I
(14)(23), I
We know these are subgroups because they are their own inverse. (Proper)
(1)(3)(24), I
(2)(4)(13), I
Order 4: (1234),(1432),(13)(24), I
(12)(34),(13)(24),(14)(23),I
These subgroups are all closed, have inverses, an identity, and are associative.
(Non-trivial)
(1)(3)(24),(13)(24),(13)(2)(4),I
The symmetries of a square
are a dihedral group which appear frequently in art and nature, which is
why we chose to analyze it. Now I had done some math and could try
and relate it to the snow covered mountains. At first I labeled the
corners of the square using four different shades of white to represent
the different colors of snow a skier might see depending on the shadow
being made, due to placement of the sun and trees. This was quite
simple because now instead of numbers as the group, I had specific colors
where the number previously existed. I decided to look at it from
a shadow perspective and try to define each time a day by one of the eight
elements. I was trying to prove that with any movement, no matter
how complicated, the outcome was equivalent to one of the eight elements
of the Dihedral group above, numbers or colors. The part I had a
problem with, in this model, was the fact that the ski slope is not a square
and therefore does not have the symmetry I needed it to. I had tried
many ways to relate the shadows from the sun hitting the ski slope at different
angles, or with different terrain, but because the symmetry is different
I couldn't go any farther. Many times I would get to a conclusion
and realize that I couldn't put trees in an area for one shadow, and not
the other. The other aspect that was hard to put in was when an element
was closed. At first I was unsure how to show this, but then I realized
I might be able to illustrate the parenthesis as leveling out along the
slope. I again ran into trouble modeling all eight elements according
to this group. So instead of dwelling on this issue we decided to
look at the mapping in another way. We noticed that we could look
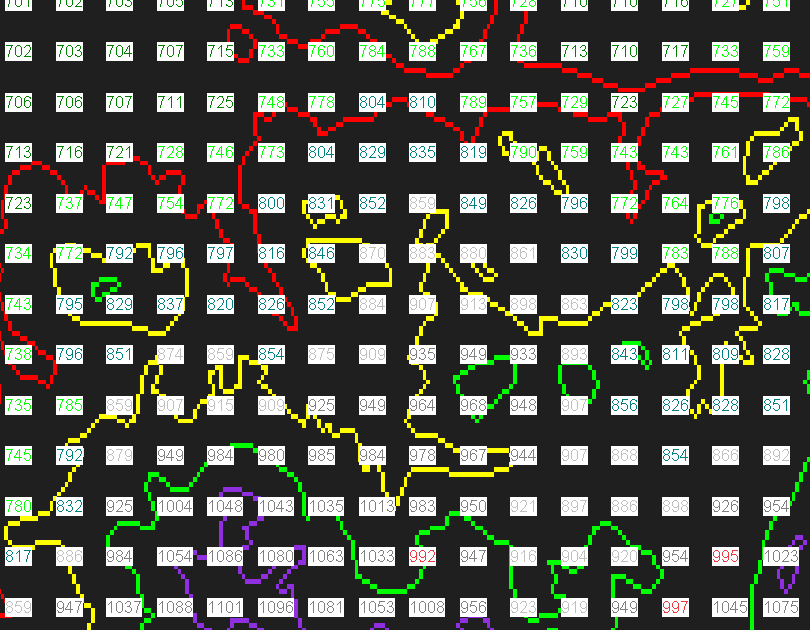
at the elevations of a mountain using Visual Terrain. I labeled parts
of Steamboat Colorado on the map below and then the program interpolated
the rest.
Map: Elevation of Steamboat Colorado, (700 means 7000)
 .
.
From this map I was able to use Visual Animator and make a 3-D map of
the terrain, as shown below.
Map: 3-D Steamboat Colorado

From this map you can see
some of the shadowing I was talking about. Depending on such factors
as where you were on the mountain, what time of day, and the terrain,
different shadows could be seen. In this program I was able to change
the view by moving the target and the camera, so I could shift the shadows
that are illustrated in this map. To remember the elevations I had
to choose colors for the contour lines that were visible and definable,
so I went with as many basic colors as I could. Then when I was choosing
to color the 3-D map I chose the summer color schema. Can I relate
this all back to what I originally was thinking about, colors?
Yes, I can. I went
back to my group of the square symmetry and made a lattice. A lattice
is another way to show relationships between the various elements or subgroups
in a group.
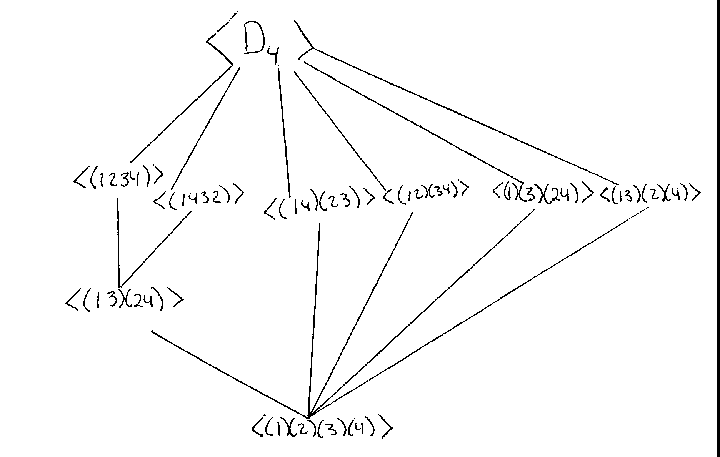
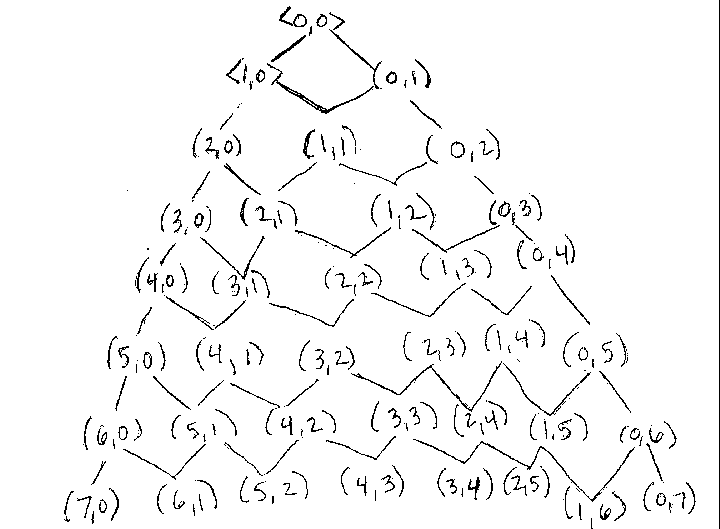
This illustration looks like something we have all seen before, but probably don't remember, and that is Pascal's Triangle.
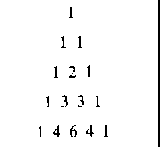
If I were to overlay Pascal's
triangle over my lattice of two colors it would fit perfectly because they
are mathematically related through binomials. Pascal's triangle gives
the coefficients while the color lattice gives the powers for the x and
y coordinates. For example:
the third row of Pascal's triangle is 1 2 1, and the third
row of the 2-color lattice is (2,0) (1,1) (0,2). Now
using a form of the equation x^2 + 2xy + y^2, where the powers change according
to the elements in the 2-color lattice. (2,0) is the 1 in Pascal's
triangle, and is therefore x^2, (1,1) is the 2 in Pascal's triangle,
and is therefore 2x^1y^1, and (0,2) is the 1 on the right side of Pascal's
triangle, therefore it is y^2. If we skip down and look at row 4,
the equation above will work its way in from x^4 to y^4. The 2-color
lattice is a way of tracking the coefficients. This shows
that we could use a Binomial Color guide where numbers are listed rather
than colors, like on the color formula guide. The binomial equation
used to determine an element in Pascal's triangle is n!/(r!(n-r)!) where
n is the row number starting at 0 and r is the position of the element
in each row starting at 0, which is now related to the 2-color lattice
I have made. Since the color schemes are split into 3 main categories,
in some programs it is blue, green, and red, while in others it is hue,
saturation, and value, each of which can range from 0 to 255, the example
above is a simplification of this where one category is held at 0 and the
other two can range from 0 to 255. At the point 000 the color is
black and as long as one stays at 0 the other two have to change by almost
100 to get a significant color change. Adobe Photo shop uses Pantone
colors, which I was able to obtain a guide for. Through a function
one could choose a four color mode or a three color mode. Since the
color guide I had was four colors I chose to the CYMK mode, where C is
cyan, Y is yellow, M is magenta, and K is black. I then tested out
this theory of choosing a color by numbers. I chose a simple one
that holds in this case two colors constant, but I still had on the screen
R,G,B so I assumed since I no longer had green that I could replace it
with the yellow number. Pantone gave the percentage of yellow as
62.5 and Blue as 37.5. I had to round up or down because the computer
would only take integers, but I put in for R =0, G=159, and B=96, and I
came up with a match for the color of Pantone 361U.
I found this project to
be very interesting and helpful. I had fun doing the project so I
spent more time learning about the tools, making mistakes, and learning
the concepts that I previously had trouble with. My confidence working
with computers has greatly increased. I would have never thought
that through the semester I would have integrated skiing, math, mapping,
and colors, but I did.
Text References
Childs, L. (1995). A Concrete Introduction
to Higher Algebra. (2nd Ed.) New York, NY: Springer.
Gallian, J. (1998). Contemporary Abstract
Algebra. (4th Ed.) Boston: Houghton Mifflin Co.
Mackiw, G. (1985). Applications of Abstract
Algebra. New York, NY: John Wiley & Sons.
Computer Programs
Digital Mapping software
Map Edit
Adobe Photo shop
Visual Terrain and Animator
Netscape Communicator