
ASSUME THE EARTH MODEL TO BE A SPHERE OF CIRCUMFERENCE 25,000 MILES.
QUESTION: WHAT IS THE LENGTH OF A DEGREE OF A MERIDIAN??
All meridians are halves of great circles. So, the length of one degree is 25,000/360 or 12,500/180 = 69.44 (approximately) miles. One degree measured along a meridian tells you how far north or south you are of the equator. So, this also is the length of one degree of latitude. Note that along a single meridian, every point will have different latitude (along a single parallel, every point will have the same latitude).
QUESTION: WHAT IS THE LENGTH OF A DEGREE OF A PARALLEL??
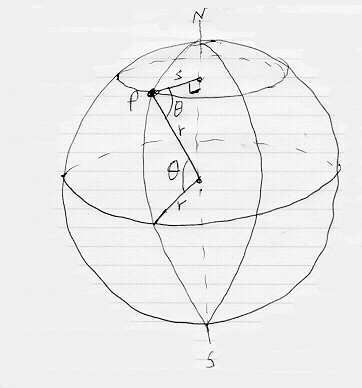
One parallel is a great circle. All other parallels are small circles. So, the length of a degree of a parallel measured along the equator is, as above, 69.44 miles. Along all other parallels, it depends on the size of the small circle. For the following sequence of steps, please refer to the figure below.
A RELATED QUESTION:
AT WHAT LATITUDE IS THE LENGTH OF ONE DEGREE OF LONGITUDE EXACTLY HALF THAT OF ONE DEGREE OF LONGITUDE MEASURED AT THE EQUATOR?
At latitude 60 degrees…the radius s is half the length of the radius r; cos 60 =0.5.
Or, using the calculations above,
Half of 69.44 is 34.72. So, we need to have 2*pi*s/360=34.72; solving for s, s=1989.311144993; but also, s=3979 cos X. So, cos X = 1989.311144993/3979=0.499952537068; X=60.00.
This same strategy would then work not only for "half" but for any other fraction.