THE CENTROID AS A MEASURE OF A SCATTER OF DOTS
Case 1: Suppose the coordinates for all dots in the scatter are known.
(x1, y1), …, (xn, yn).
Then, the centroid is calculated as a point with coordinates:
((x1+…+xn)/n, (y1+…+yn)/n)
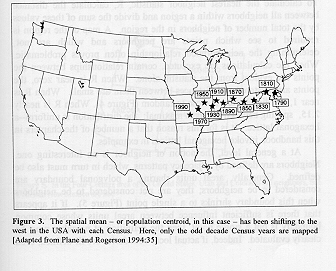
If one has a scatter of dots for a number of different time periods, and wishes to track the migration of the dot pattern over time, it can be useful to map the centroid for each time period and follow changes in the centroid over time.
Case 2: Suppose not all the coordinates for all dots in the scatter are known.
When not all the coordinates are known, assign some other (perhaps nearby) value to the dots. For example, if values for a particular variable are given for each state in a country, but not for the individuals within the state, assign to each individual the value of the geometric centroid of the state (often can be read from a GIS). Then, calculate the centroid as above. This sort of grouping of data is used in various types of statistical measures. People who focus on spatial statistics often refer to this as a "spatial mean". Others might view it as a standard calculation of the centroid using available information, with possible error caused by grouping.
The map below from Practical Handbook of Spatial Statistics (S. Arlinghaus et al., CRC Press), Chapter 2 by Vasiliev, illustrates this idea that can be applied in a variety of different contexts.
