Elementary plane geometry was long a favorite of mathematicians and amateurs alike, but has fallen
a bit into disfavor nowadays. In the nineteenth century it was so popular a subject that
the comprehensive index of scientific papers put out by the Royal Society in London, England, explicitly
excluded over 600 papers on triangles and conic sections from its index volume for Pure Mathematics
which already comprised over 32,000 items.
It is of interest that one can view many of the theorems of plane geometry from a point of view
provided by the Discrete Fourier Transform (DFT) and that this leads on to some other results on
circulant matrices, smooth interpolation of point distributions in the plane, zeroes of polynomials,
and even a connection with quantum bits and the Heisenberg-Weyl algebra
as it turns up in signal processing.
In addition the geometric use of the DFT provides some beautiful diagrams for mechanical problems.
What is plane geometry? Start with the two-dimensional plane, which we'll think of as having
as coordinates complex numbers $x + \ii y \in \cplx$. Since theorems about
intervals defined by their two end-points are perhaps not too interesting, we'll start with the
geometry of triangles. There are several common classes of theorems about triangles.
I'll distinguish three types to begin with: Coincidence, Collinearity and Equilaterality.
To see a note on some new technology behind this document click on
the following up-arrow. To hide it again click on the corresponding down-arrow when it is shown
.
This pairing of up- and down-arrows is used to Show or Hide asides or details of equations
that may be a little long-winded unless a reader wants more detail.
Theorems of Coincidence
Triangle Medians
The first example is a triangle and the lines from the vertices to the bisection points
of opposite sides, which lines are called the medians. Pairwise, they intersect in 3 new points.
The first example theorem says these three points coincide. The point of common
intersection is called the centroid of the triangle, conventionally denoted $G$.
The figure below shows this.
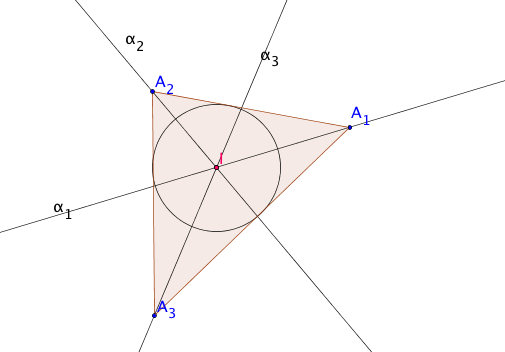
Triangle Angle Bisectors
The second example is a triangle and the lines from the vertices that bisect the angles.
Pairwise, they intersect in 3 points. The second theorem says these three points coincide.
The point of coincidence is the the center of the incircle $I$ of the triangle.
The angle bisectors are the lines labelled $\alpha_1$, $\alpha_2$ and
$\alpha_3$, and the red point $I$ marks the three coincident pairwise
intersections of $\alpha_1$, $\alpha_2$ and $\alpha_3$ at the incenter.
The blue vertices $A_1$, $A_2$ and $A_3$ can be dragged about to change
the triangle in the interactive pop-up version.
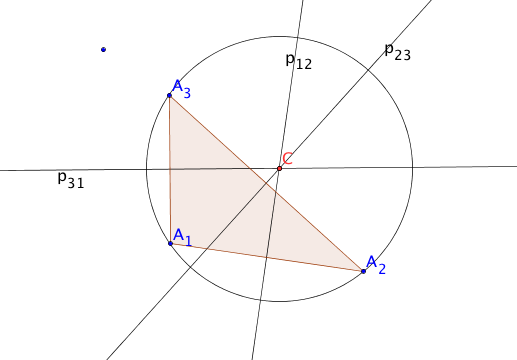
Triangle Perpendicular Bisectors
A third example is a triangle and the lines that perpendicularly bisect the sides.
Again the pairwise intersections coincide, at the circumcenter $C$.
The lines $p_{12}$, $p_{23}$ and $p_{31}$ are the respective perpendicular bisectors
of the triangle sides $A_1A_2$, $A_2A_3$ and $A_3A_1$.
Pairwise, they intersect in 3 points. The theorem says these three points
coincide as the red point $C$, the circumcenter.
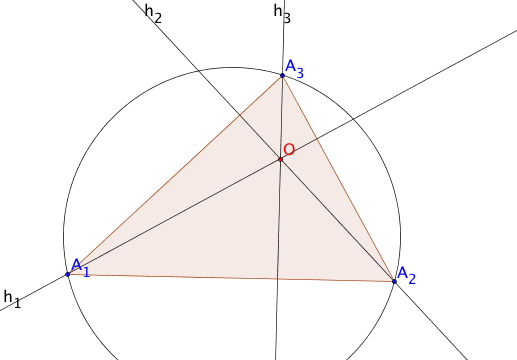
Triangle Altitudes
Again we have a coincidence for the altitudes of a triangle, the lines drawn from the
vertices perpendicular to the opposite sides. The point of coincidence is called the orthocenter $O$.
The lines $h_{1}$, $h_{2}$ and $h_{3}$ are the
respective altitudes from $A_1$, $A_2$ abd $A_3$. Pairwise, they intersect in 3 points.
The theorem says these three points coincide as the red point $O$, the orthocenter.
Note that it is not the center of any particular circle we have already identified,
but it is the intersection of perpendiculars dropped from points on the circumcircle to
the opposite sides of the triangle, which are chords of that circle.
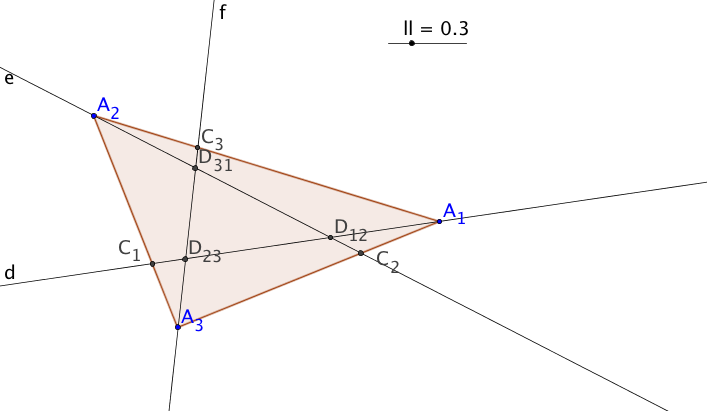
Triangle Cevians
Just to show that not every natural construction leads to a coincidence of pairwise intersetions,
note this is not so for arbitrary Cevians of a triangle, which are lines from the vertices
to points on the opposite sides.
The case illustrated in the diagram is that in which the
point on the opposite side is a constant proportion of the way along from each vertex to the
next one in the cycle $A_1$, $A_2$ , $A_3$. The initial case in the diagram is for the proportion
$\frac13$ but this can be adjusted with the slider at the top right of the diagram by dragging
the point along. Remark that for the value $\frac12$ we are back at the first case above
of Triangle Medians, and we do have coincidence.
Coincidence theorems
The prime example of a coincidence theorem is probably that concerning the Euler line.
The remarkable fact, first noted by Euler, is that the circumcenter $C$, the centroid $G$
and the orthocenter $O$ are collinear for any triangle with vertices $A_1$, $A_2$ and $A_3$.
The medians are in green and the perpendicular bisectors in blue.
The line through them is shown in orange so as to stand out a bit in the figure below.
Equilaterality theorems
Napoleon's Theorem
Napoleon's theorem, though probably not directly due to the emperor
himself, has long been eponymous with him. In its simplest form it
says that if one constructs on each side of a nondegenerate plane
triangle, and external to it, an equilateral triangle of base equal
to the side, and then takes the three centroids of the resulting
triangles, then these points are the vertices of an equilateral
triangle. That is you start with an arbitrary triangle, construct
three new points in a specified way and the resulting points are the
vertices of an equilateral triangle. This is illustrated in the
accompanying diagrams, which actually shows that a similar construction
using triangles on the other sides of the triangle sides also leads
to a different equilateral triangle.
The equilateral triangles constructed externally on the sides of the
triangles are given yellow backgrounds, and have centroids marked in
red. The three centroids make the vertices of an equilateral triangle
given an orange tinge.
The internal triangles constructed externally on the sides of the
triangles are given green backgrounds, and have centroids marked in
red. The three centroids make the vertices of an equilateral triangle
given a green tinge.
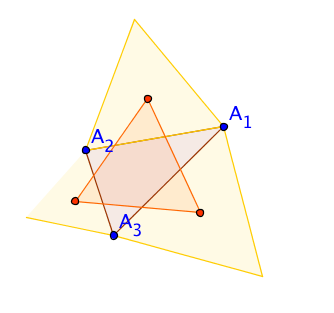
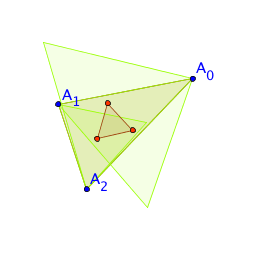
There is a rather more general form of the theorem which
will be seen as a consequence of what will be proved below. It states that
the results of a whole class of constructions which are specified to
be made on the edges of an arbitrary nondegenerate plane $N$-gon
will be a regular $N$-gon of a specific type.
Morley's Theorem
What was hailed when it was discovered as the first really new advance in plane
geometry since the Greeks became known as Morley's Miracle. It was found in about
1900 but not really published by its discoverer Frank Morley until many years
later. Many proofs of it have appeared, a notable recent one of great generality
being due to Alain Connes. It can be thought to be related to the approach
explored below.
Morley's basic concistruction is:
or any non-degenerate triangle consider the internal angle trisectors. Then consider
the pairwise intersections of adjacent ones. The resulting points are the vertices of
an equilateral triangle. Again a diagram shows the remarkable assertion nicely.
There is an equilateral triangle from the internal trisectors shown in green.
The triangle is given a reddish tinge.
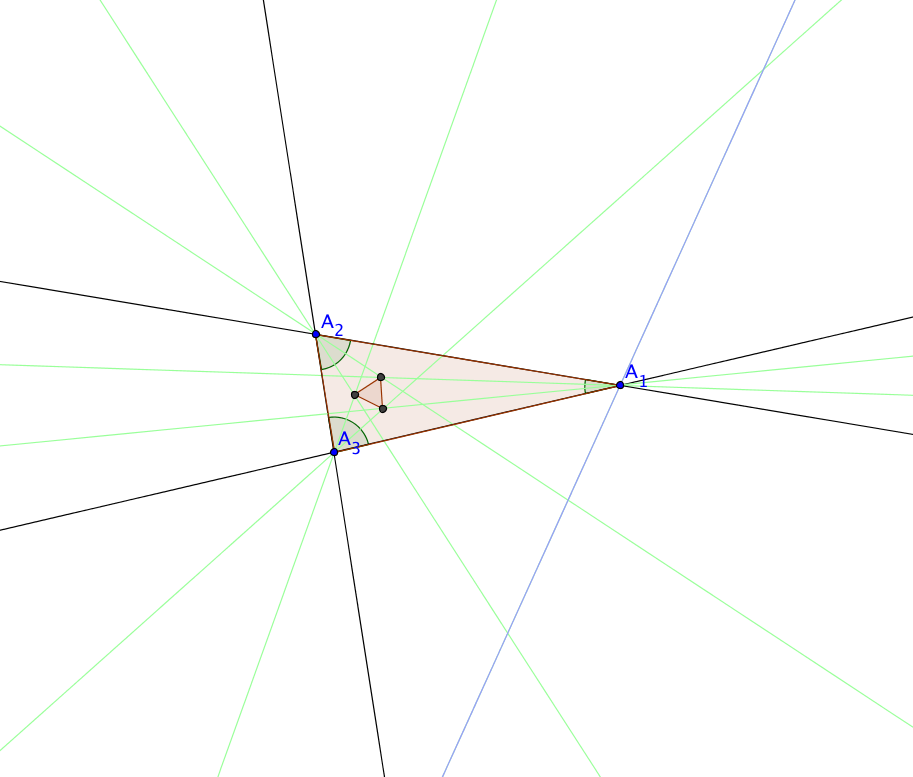
There is even more to be found from considering angle trisectors of
which there are two for each angle; indeed at each vertex there are
two angles the internal and the external. By considering all suitable
combinations of angles and trisectors, in fact one finds $18$ equilateral
Morley triangles assocciated to a given triangle. Liouville and others
later went on to consider other fractions of polygon angles and more
general constructions. Again a diagram can help.
In the case shown there is the equilateral triangle from the internal trisectors, and
another one from external trisectors is show as well. The internal
trisectors are shown in green, the external trisectors are shown in
lilac.
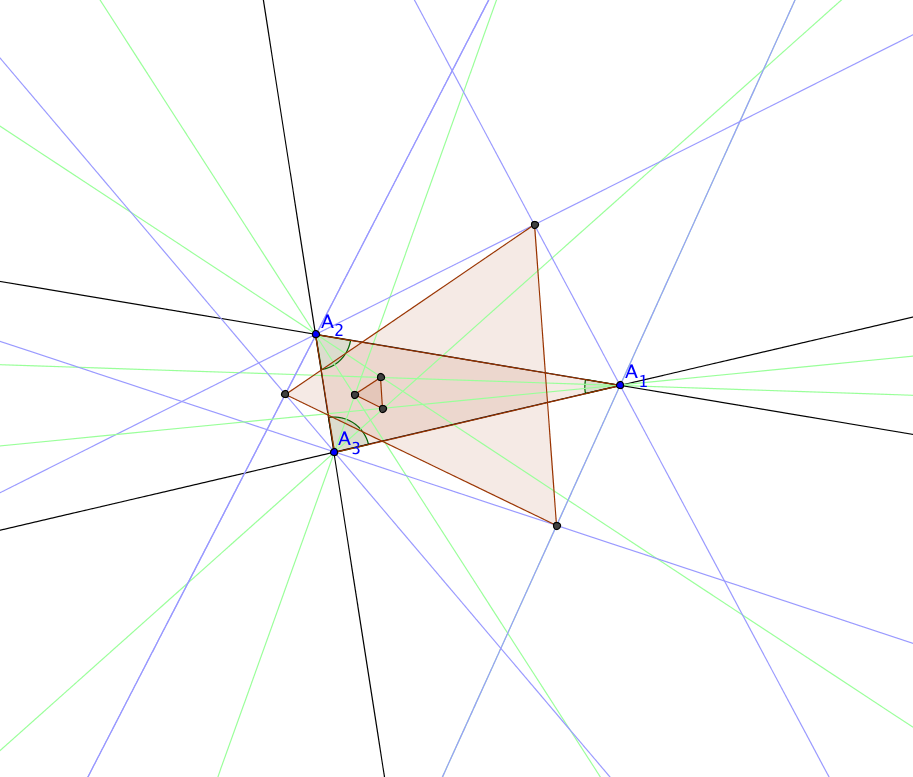
A pentagon construction
A new twentieth-century type of construction, that was devised probably around 1940
but only published in 1960 in a piece in honor of a colleague Jekuthiel Ginsburg, is due to
the American Fields medalist Jesse Douglas. He specifies a fixed construction that from
any pentagon will derive an associated convex pentagon and a pentagram.
Consider a pentagon in the plane. For that matter, we could let the points be in a space of dimension
up to 4, since 5 points can only subtend a space of at most dimension 4. However, the formalism
is simpler for the plane so that's where we'll start. The full situation will be considered later.
We are viewing the 2-dimensional plane as given
by a single complex coordinate $z = x + \ii y$. Suppose the five vertex points are $ p_1$, $p_2$,
$p_3$, $p_4$, and $p_5$; so we are given the complex vector in ${\mathbb C}^5$, a list of points,
$$ p=(p_1,p_2,p_3,p_4,p_5).$$
Since no one point of the five is distinguished, we shall consider the indices $i$
of $p_i$ modulo $5$: sums in the index are cyclic, so that, for instance, $p_{3+4} = p_2$.
Douglas suggests: Join each vertex $p_i$ to the midpoint of the edge opposite between the
points $p_{i+2}$ and $p_{i+3}$ ; then extend that line by an extra piece of length
$(1/\sqrt{5})$ of the original piece to create a new vertex $q_i$. Douglas observed that
the new pentagon $(q_1, q_2, q_3, q_4, q_5)$ is always the affine image of a convex regular
pentagon. He also remarked that if, instead, the lines to the opposite midpoints are shortened
by a similar decrement ratio of $(1/\sqrt{5})$ to give new vertices $r_i$, then
$(r_1, r_2, r_3, r_4, r_5)$ is the affine image of a regular star pentagon, commonly called a pentagram.
We interpret this in coordinates and plot sample results. We start with, say,
$ p=(p_1,p_2,p_3,p_4,p_5)$. The plots are done below using an arbitrarily chosen example, but
as usual the vertices can be dragged about in the interactive pop-up figure.
$$
p=(1.3 + 2.2 \ii, 4.4 + 1.5 \ii, 6 + 5.5 \ii, 1.5 + 4.1 \ii, 5.6 + 6.4 \ii).
$$
We see $$q_i = p_i + \left(1+\frac1{\sqrt{5}}\right)\left({\frac{1}{2}}(p_{i+2}+p_{i+3}) - p_i\right) ,$$
outlined in green in the figure.
and similarly that
$$r_i = p_i + \left(1-\frac1{\sqrt{5}}\right)\left({\frac{1}{2}}(p_{i+2}+p_{i+3}) - p_i\right) ,$$
outlined in red.
Putting all this into a diagram with all the lines drawn, which it is amusing to pull about to see
the effectiveness of the construction, we get
We see that starting from an arbitrary pentagon, a list of five points, we get by a fixed
construction two new pentagons, which are, respectively, an affine image of a standard convex pentagon
and an affine image of a standard pentagram.
Continued by:
