
Atmospheric Dynamics Modeling Group
|
Research
Paul Ullrich, Ph.D.
|
|
|
|
|
|
|
MCore is a high-order upwind finite-volume atmospheric modeling environment which incorporates a shallow-water model on a sphere, a regional weather model with both f-plane and beta-plane configurations and a 3D global non-hydrostatic model. Upwind finite-volume models do not use explicit diffusion to maintain stability, but instead can be configured with a nonlinear implicit diffusion parameterization that significantly improves conservation properties compared to other finite-volume and finite-difference techniques. Further, our global models are implemented on the cubed-sphere in order to maximize parallel performance on large-scale computing systems.
MCore is a fully non-hydrostatic global model, and so can be used for consistent simulation of small-scale flows in a global domain. This functionaltiy is made possible by a Runge-Kutta-Rosenbrock time discretization which allows coupling between the horizontal and vertical spatial operators while maintaining accuracy and efficiency of the underlying method. This model has already been used in several dynamical core intercomparison studies, and shows promise for future development into an operational global model.
Our next goal is to incorporate static and adaptive mesh refinement functionality, which will be provided by the Chombo mesh refinement framework. This will allow us to incorporate regions of very fine resolution in a global modal domain and so reduce errors normally present in coupled models by allowing fully two-way coupling between the fine and coarse domain.
|
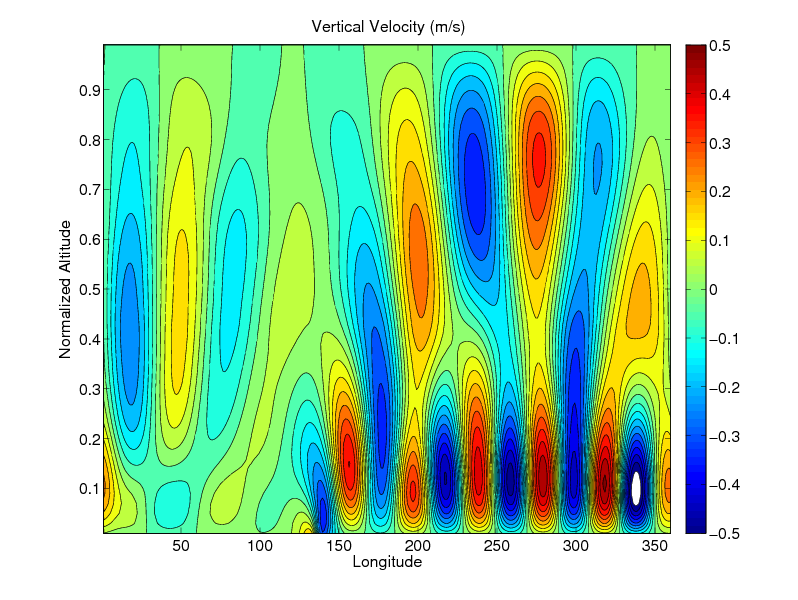
Figure: A simulation of non-hydrostatic waves triggered by a mountain range on a ``small'' planet, showing vertical velocity along the equator. The mountain range is located at 135 degrees longitude, and the atmosphere is capped at 30 km altitude.
|
| |
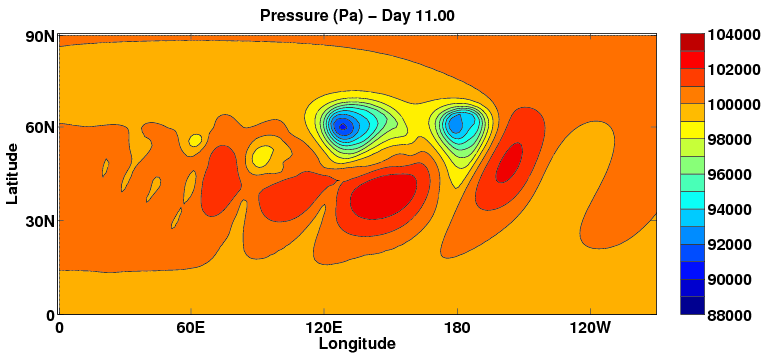
Figure: Surface pressure after 11 days for the Ullrich, Melvin, Jablonowski and Staniforth (2011) baroclinic instability under MCore's deep atmospheric configuration.
|
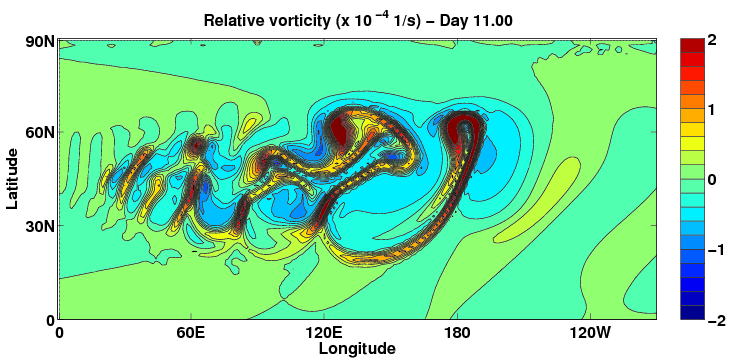
Figure: Surface vorticity after 11 days for the Ullrich, Melvin, Jablonowski and Staniforth (2011) baroclinic instability under MCore's deep atmospheric configuration.
|
Relevant Publications:
- (In Preparation)
Ullrich, P.A., C. Jablonowski and P.H. Lauritzen (2011)
"A high-order `incremental-remap'-based semi-Lagrangian dynamic core." To be submitted to J. Comp. Phys. Nov. 2011.
- (In Preparation)
Ullrich, P.A., T. Melvin, C. Jablonowski and A. Staniforth (2011) "A baroclinic wave test case for deep and shallow atmosphere atmospheric dynamical cores." To be submitted to Q. J. Roy. Met. Soc. Dec. 2011.
- (Under Revision)
Ullrich, P.A. and Jablonowski, C. (2011)
"MCore: A nonhydrostatic atmospheric dynamical core utilizing high-order finite-volume methods."
Submitted to J. Comp. Phys.
- (Link)
Ullrich, P.A. and Jablonowski, C. (2011)
"Operator-Split Runge-Kutta-Rosenbrock (RKR) Methods for Nonhydrostatic Atmospheric Models",
Mon. Wea. Rev.
- (Link)
Ullrich, P.A., C. Jablonowski and B. van Leer (2010)
"High-order finite-volume models for the shallow-water equations on the sphere",
J. Comp. Phys., Vol. 229, Issue 17, pp. 6104-6134, DOI: 10.1016/j.jcp.2010.04.044.
|
|
|
The problem of 2D tracer advection on the sphere is extremely important in modeling of geophysical fluids, and has been tackled using a variety of approaches. A class of popular approaches for tracer advection include `incremental remap' or semi-Lagrangian-type schemes. The upstream version of this scheme consists of a deformation step, where a structured Eulerian grid is tracked upstream to a ``source grid,'' and a remapping step, where tracer fields are remapped onto the source grid to give the updated tracer mass in each cell. These schemes achieve high-order accuracy without the need for multi-stage integration in time, are capable of large time steps and are very efficient when transporting multiple tracers.
Our work on semi-Lagrangian tracer transport schemes has led to the development of the Conservative Semi-Lagrangian Multi-tracer (CSLAM) scheme for efficient and accurate tracer transport. This work will be incorporated in the next iteration of NCAR's spectral element dynamical core. This work has been in close collaboration with Dr. Peter Lauritzen.
|
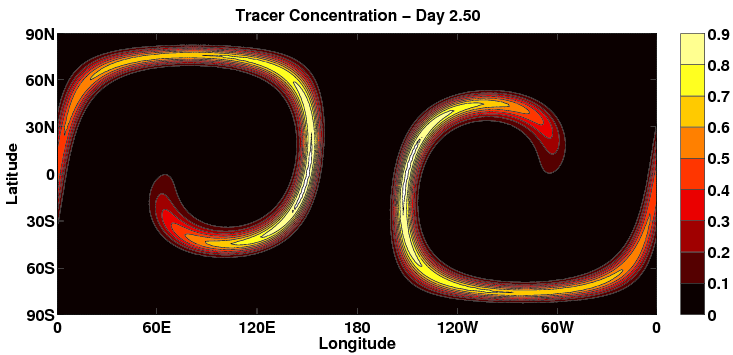
Figure: Tracer advection using quadrature-based flux-form CSLAM (Ullrich et al., 2011) for the deformational flow test of Nair et al. (2010) with Gaussian hills initial conditions after 2.5 days with a shape-preserving filter.
|
Relevant Publications:
- (In Preparation)
Lauritzen, P. H., Andronova, N., Bosler, P. A., Calhoun, D., Enomoto, T., Dong, L., Dubey, S., Guba, O., Hansen, A. B., Jablonowski, C., Juang, H.-M. H., Kaas, E., Kent, J., Muller, R., Penner, J. E., Prather, M. J., Reinert, D., Skamarock, W. C., Sorensen, B., Taylor, M. A., Ullrich, P. A. and White J. B. III, (2011): "A standard test case suite for 2D linear transport on the sphere: results from 17 state-of-the-art schemes." To be submitted to Geoscientific Model Development.
- (In Preparation)
Ullrich, P.A., C. Jablonowski and P.H. Lauritzen (2011)
"A high-order `incremental-remap'-based semi-Lagrangian dynamic core." To be submitted to J. Comp. Phys. Nov. 2011.
- (In Review)
Ullrich, P.A., P.H. Lauritzen and C. Jablonowski (2011)
"Some considerations for high-order `incremental remap'-based transport schemes: edges, reconstructions and area integration"
Submitted to J. Comp. Phys.
- (Link)
Lauritzen, P.H., R.D. Nair and P.A. Ullrich (2010)
"A conservative semi-Lagrangian multi-tracer transport scheme (CSLAM) on the cubed-sphere grid",
J. Comp. Phys. Vol. 229, Issue 5, pp. 1401--1424, DOI: 10.1016/j.jcp.2009.10.036.
Book Chapters:
- (Link) Lauritzen, P.H., P.A. Ullrich and R.D. Nair (2011) "Atmospheric transport schemes: Desirable properties and a semi-Lagrangian view on finite-volume discretizations." Chapter in the Springer book 'Numerical Techniques for Global Atmospheric Models.'
|
|
|
Computing power has increased exponentially over the past decade, stimulating a significant burst of new research focused on developing software that can take advantage of the rapidly advancing hardware. In particular, it has become increasingly important to design atmospheric models which are capable of scaling on systems with tens to hundreds of thousands of processors. Hence, significant effort has been directed to the study and application of modern numerical techniques to simulating the atmosphere.
The most popular modern schemes include discontinuous Galerkin, spectral element and finite-volume methods. These methods all have well known advantages and disadvantages, however the comparative performance and accuracy of these methods for smooth, well-resolved problems is largely missing from the literature. Although the modeling community has pressed forward with the usage of these methods in dynamical models, there remains a significant number of unanswered mathematical problems that remain to be answered. Without a rigorous mathematical foundation, spurious errors are bound to arise in geophysical models which may pollute the solution in unexpected ways.
Our work on numerical analysis aims to close these gaps in the understanding of these methods, and establish a solid mathematical foundation for the development of atmospheric dynamical cores.
|
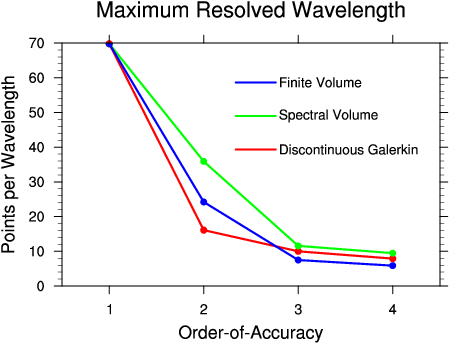
Figure: Shortest wave mode which is resolved to at most 0.5 percent error in the advective dispersion relation of the numerical method. Wave modes below this threshold are considered poorly resolved by the numerical method.
|
Relevant Publications:
- (In Preparation)
Ullrich, P.A., J. Whitehead, C. Jablonowski and M.A. Taylor (2011) "A stability analysis of advection and diffusion in the Community Atmosphere Model Spectral Element (CAM-SE) model." To be submitted to J. Comp. Phys. Dec. 2011.
- (Link)
Ullrich, P.A. and Jablonowski, C. (2010)
"An analysis of 1D finite-volume methods for geophysical problems on refined grids",
J. Comp. Phys., Volume 230, Issue 3, pp. 706-725, DOI: 10.1016/j.jcp.2010.10.014.
|
|
|
Adaptive Mesh Refinement (AMR) techniques provide an attractive framework for atmospheric flows since they allow an improved resolution in limited regions without requiring a fine grid resolution throughout the entire model domain. The model regions at high resolution are kept at a minimum and can be individually tailored towards the research problem associated with atmospheric model simulations.
The climate system is characterized by complex nonlinear interactions over a broad range of temporal and spatial scales. Our research objective is to determine how these multi-scales interact and how to use enabling computational tools to mathematically represent scale interactions in climate models. The research focuses in particular on scale interactions in the so-called dynamical core of Atmospheric General Circulation Models (GCM). The dynamical core refers to the fluid dynamics component of a GCM and encompasses the numerical methods used to solve the equations of motion on the resolved scales. The research explores how Adaptive Mesh Refinement (AMR) and other variable resolution grid techniques allow high resolution meshes in regions of interest like the eye of a tropical cyclone or over mountainous terrain. It thereby suggests pathways how to bridge the scale discrepancies between local, regional and global phenomena, a key frontier in climate modeling.
The variable-resolution approach is focused on cubed-sphere computational meshes that have the potential to become a standard in future GCMs. Cubed-sphere grids offer an almost uniform grid point coverage on the sphere. They deliver high performance and almost perfect scaling characteristics on massively parallel computer architectures. The grid is ideally suited for local grid refinements that are based on DoE's AMR software framework Chombo from the Lawrence Berkeley National Laboratory (LBNL). Chombo is under development by DoE's Applied Partial Differential Equations Center (APDEC) under the leadership of our collaborator Dr. Phillip Colella. Both hydrostatic and nonhydrostatic dynamical core designs are developed, implemented and assessed in our team using high-order conservative and oscillation-free finite-volume numerical schemes. In addition, we investigate the numerical schemes in a 2d shallow-water framework that serves as an ideal testbed for 3d model developments. At a later stage our simulations will also involve an in-depth investigation of the validity of physical parameterizations at different spatial scales. The latter will be done in close collaboration with the National Center for Atmospheric Research (NCAR).
Relevant Publications:
- Check back soon! We expect to submit a manuscript on this topic in early 2012.
|
|
|
The Geometrically Exact Conservative Remapping (GECoRe) package has been developed as a new toolset for high-order conservative remapping of scalar fields between the latitude-longitude and cubed-sphere grid. This work has been in collaboration with Dr. Peter Lauritzen.
|
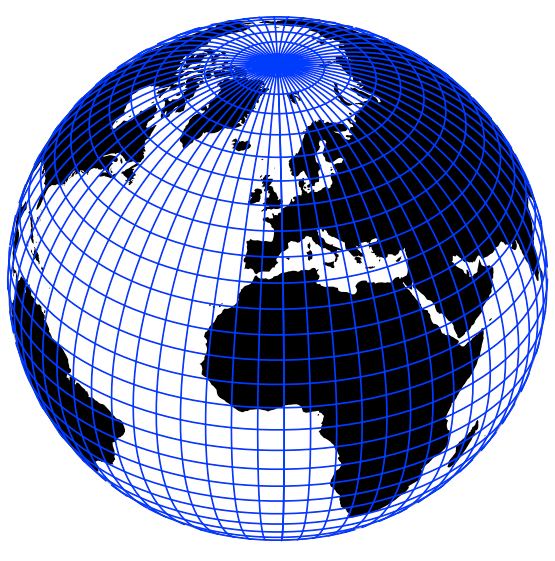 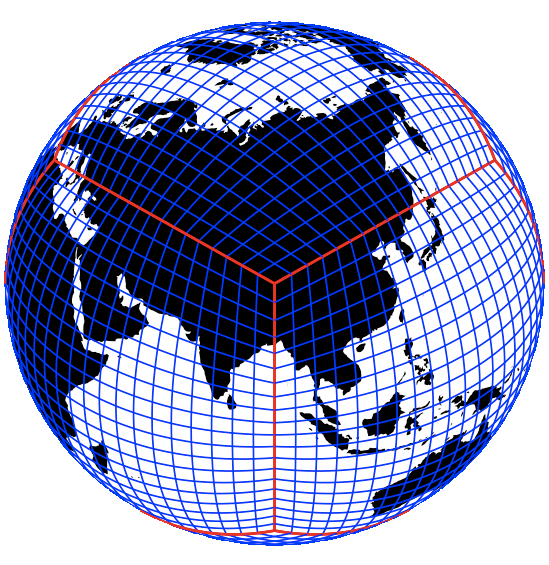
Figure: The cubed-sphere grid is a leading candidate for next-generation global models due to its quasi-uniformity and rectangular grid structure. These properties lead to effective parallelization of models built on the cubed-sphere and eases the implementation of high-order numerical methods.
|
Relevant Publications:
- (Link)
Ullrich, P.A., P.H. Lauritzen and C. Jablonowski (2009)
"Geometrically Exact Conservative Remapping (GECoRe):
Regular latitude-longitude and cubed-sphere grids",
Mon. Wea. Rev. Vol. 137, No. 6, pp. 1721--1741.
|
|

