Postcript Figures are available here:

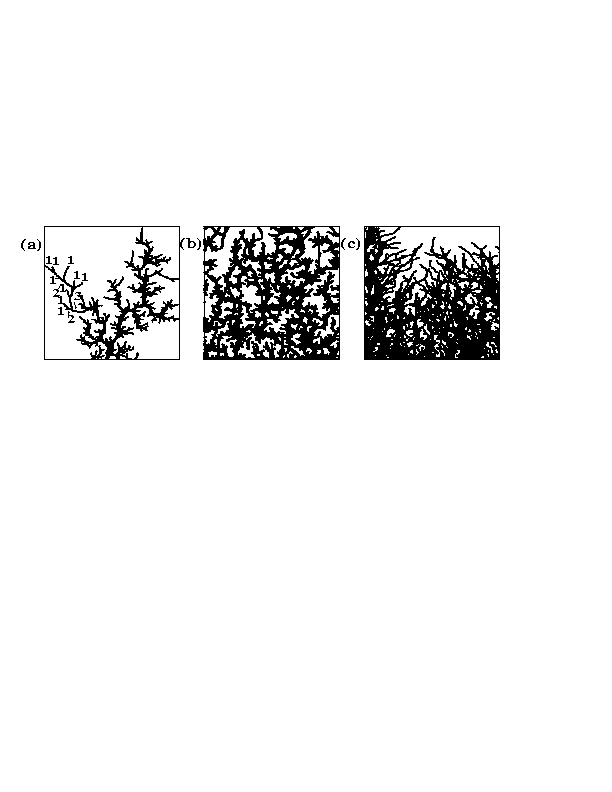
Snapshots of northbound vortex pathways: (a) Hortonian (when the pinning force, f_p, is stronger than the vortex-vortex repulsion f^{vv} ; i.e., at low B and high f_p); (b) braided (when f_p is comparable to f^{vv}: B \approx 3 B_{\phi} / 2 ); and (c) dense (when pinning is much weaker than f^{vv}; i.e., for B > 2 B_{\phi}, or at any field for low f_p). Here, n_p = 0.75 / \lambda^2. Here (a) shows a (low local B) flux-front region and (b) shows an intermediate-B section of the same sample.
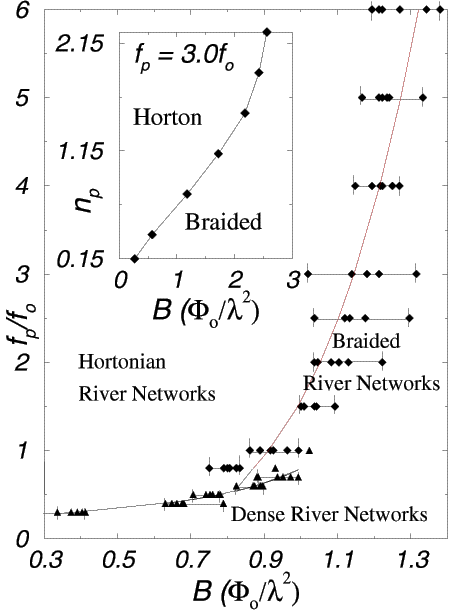
The vortex river network morphological phase diagram for pinning force, f_p, versus magnetic field, B, for n_p=0.75 / \lambda^2 (thus, here B_{\phi} = 0.75 \Phi_0 / \lambda^2). In regions of very low pinning force f_p, dense (space-filling for t \rightarrow \inf) vortex river networks dominate. For higher pinning f_p's, the Hortonian rivers become braided when B grows. For samples with higher pinning, it is the initial front (with low local density of field lines B, B < 3 B_{\phi} / 2, and thus dominant pinning force f_p) which branches out in a Hortonian manner. Behind this initial front follows the (intermediate-B) braided region. Further behind, follows the (large-B) dense-flux regime. The inset shows the shift in the Horton-braided boundary f_p = 3 f_0 as the pinning density, n_p, is changed. As n_p is increased, the Horton-braided boundary shifts towards higher B. The broad crossover boundaries are in the region of triangles and rhombuses. The (power-law fit) lines are just guides to the eye. The dense-braided crossover at high-fields (dashed) is an extrapolation of the power-law fit for low fields; the former is very difficult to compute because it requires a large number of vortices monitored over very long times.
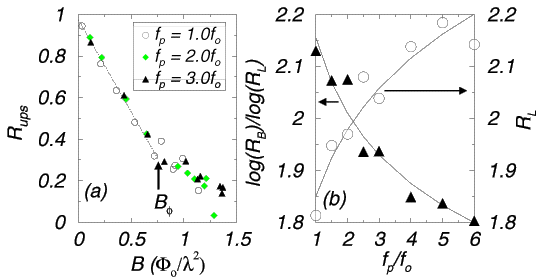
(a) Fraction R_{ups} of unoccupied pinning sites (ups) versus B for six samples with different f_p's. (and five realizations of disorder for each f_p). We find a change in the rate at which pins become occupied with increasing B: it decreases noticeably for B > B_{\phi}. (b) The length ratio R_L and fractal dimension D_F = d_c \log{R_B} / \log{R_L}, versus the pinning force, f_p. Here, the average stream dimension, d_c, is one. Only the trends in R_L and D_F can be observed here because their error bars are +/- 0.05. The lines are power-law best fit curves, which only provide a guide to the eye. The formula for D_F, namely D_F / d_c = \log{R_L} / \log{R_B}, gives values slightly above the space-filling value of 2, because it assumes that Horton's laws hold at all length scales, while our vortex basins only span a very limited range of length scales. Open circles: The length ratio R_{L} versus the pinning force f_p. Filled triangles: The ratio D_f / d_c versus f_p. The lines are best fit curves.
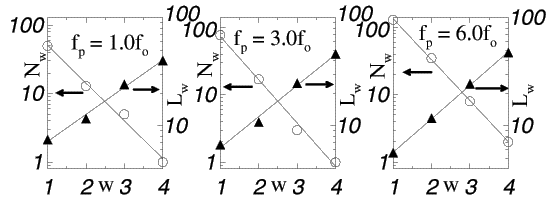
The number of streams N_w of order w, and their lenghts L_w, for vortex river networks with three different pinning forces f_p. Six different f_p's gave virtually identical plots---all obeying Horton's laws. Open circles indicate the number N_w of streams with order number w. Filled triangles indicate the average length L_w of streams with order number w.