Phase Locking, Devil's Staircases, Farey Trees, and
Arnold's Tongues in Driven Vortex Lattices with Periodic Pinning
C. Reichhardt and Franco Nori,
Physical Review Letters, 82, 414 (1999).
Using numerical simulations, we observe phase locking,
Arnold tongues, Farey trees, and Devil's staircases
for vortex lattices driven at varying angles with respect
to an underlying superconducting periodic pinning array.
This rich structure should be observable in transport measurements.
The transverse V(I) curves have a Devil's staircase structure,
with plateaus occurring near the driving angles
along symmetry directions of the pinning array.
Each of the plateaus corresponds to a different dynamical phase
with a distinctive vortex structure and flow pattern.
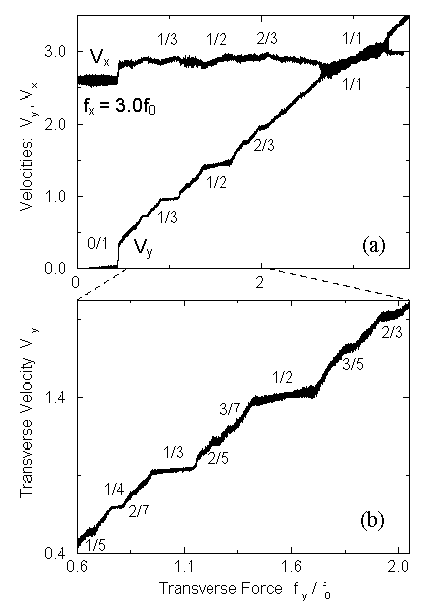 (a)
Average longitudinal V_x (upper curve) and transverse V_y
velocities versus the transverse driving force f_y
for a 36 \lambda \times 36 \lambda sample with
a square pinning array,
density of field lines B satisfying B/B_{\phi} = 1.062,
matching field B_{\phi} = 0.4 \Phi_0 / \lambda^2,
density of pinning sites n_p = 0.4 / \lambda^2,
f_p = 2.5 f_0, a = 1.57 \ lambda, and r_p = 0.3 \ lambda.
f_x is fixed at f_x = 3.0 f_0. Plateaus are seen in
V_y near values where f_y / f_x = p/q, where p and q
are integers. The largest plateaus
(at 0/1, 1/3, 1/2, 2/3, and 1/1) are clearly seen.
(b)
shows a blow up of V_y from (a), for f_y = 0.6 f_0
to 2.1 f_0, where additional plateaus at 1/5, 1/4, 2/5, 3/7, and
3/5 can be seen more clearly.
The overall structure in V_y
is that of a Devil's staircase.
(a)
Average longitudinal V_x (upper curve) and transverse V_y
velocities versus the transverse driving force f_y
for a 36 \lambda \times 36 \lambda sample with
a square pinning array,
density of field lines B satisfying B/B_{\phi} = 1.062,
matching field B_{\phi} = 0.4 \Phi_0 / \lambda^2,
density of pinning sites n_p = 0.4 / \lambda^2,
f_p = 2.5 f_0, a = 1.57 \ lambda, and r_p = 0.3 \ lambda.
f_x is fixed at f_x = 3.0 f_0. Plateaus are seen in
V_y near values where f_y / f_x = p/q, where p and q
are integers. The largest plateaus
(at 0/1, 1/3, 1/2, 2/3, and 1/1) are clearly seen.
(b)
shows a blow up of V_y from (a), for f_y = 0.6 f_0
to 2.1 f_0, where additional plateaus at 1/5, 1/4, 2/5, 3/7, and
3/5 can be seen more clearly.
The overall structure in V_y
is that of a Devil's staircase.
 Vortex trajectories for a subset of the system used in Fig. 1
at the plateau regions
(a) f_y / f_x = 0,
(b) f_y / f_x = 1/2, and
(d) f_y / f_x = 1/1, and at the non-plateau region
(c) f_y / f_x = 2 \pi / 11 = 0.571...
At the plateau regions, the vortices move in 1D channels,
periodically along the pinning rows; while at the non-plateau
regions the vortices exhibit quasiperiodic trajectories.
Vortex trajectories for a subset of the system used in Fig. 1
at the plateau regions
(a) f_y / f_x = 0,
(b) f_y / f_x = 1/2, and
(d) f_y / f_x = 1/1, and at the non-plateau region
(c) f_y / f_x = 2 \pi / 11 = 0.571...
At the plateau regions, the vortices move in 1D channels,
periodically along the pinning rows; while at the non-plateau
regions the vortices exhibit quasiperiodic trajectories.
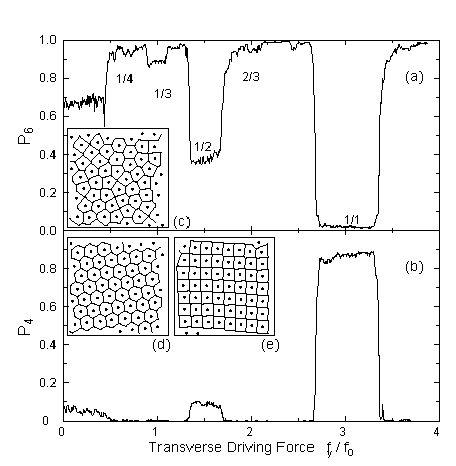 The fraction of (a) six-fold P_6 and (b) four-fold P_4
coordinated vortices versus transverse driving force
f_y, for the same system as in Fig. 1.
Large drops in P_6 can be seen at f_y^c,
as well as at the 1/2 and 1/1 locking regions.
Smaller dips in P_6 can be seen at the
1/4, 1/3, and 2/3 plateaus regions.
At the 1/1 transition P_4 rises to approximately 0.9
indicating a transition to a square VL.
In (c,d,e) both the vortex positions and Voronoi polygons
for a subset of the VL can be seen for:
(c) the 1/2 locking region, where a disordered VL is observed;
(d) right before the 1/1 plateau, with a triangular VL; and
(e) at the 1/1 plateau, with a square VL.
The fraction of (a) six-fold P_6 and (b) four-fold P_4
coordinated vortices versus transverse driving force
f_y, for the same system as in Fig. 1.
Large drops in P_6 can be seen at f_y^c,
as well as at the 1/2 and 1/1 locking regions.
Smaller dips in P_6 can be seen at the
1/4, 1/3, and 2/3 plateaus regions.
At the 1/1 transition P_4 rises to approximately 0.9
indicating a transition to a square VL.
In (c,d,e) both the vortex positions and Voronoi polygons
for a subset of the VL can be seen for:
(c) the 1/2 locking region, where a disordered VL is observed;
(d) right before the 1/1 plateau, with a triangular VL; and
(e) at the 1/1 plateau, with a square VL.
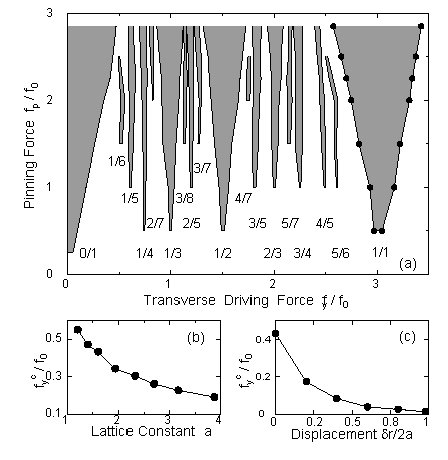 (a) Phase diagram, for the system in Fig. 1,
showing Arnold tongues (shaded);
i.e., the widths of the locking regions versus f_p.
As f_p decreases, the tongues (locking regions with
periodic trajectories) shrink. In (b,c) the width of the
first locking region
(known as f^c_y, the critical transverse force)
is shown versus pinning lattice constant a
(b) and disorder \delta r/2a (c).
(a) Phase diagram, for the system in Fig. 1,
showing Arnold tongues (shaded);
i.e., the widths of the locking regions versus f_p.
As f_p decreases, the tongues (locking regions with
periodic trajectories) shrink. In (b,c) the width of the
first locking region
(known as f^c_y, the critical transverse force)
is shown versus pinning lattice constant a
(b) and disorder \delta r/2a (c).
Postcript Figures are available here:
Manuscript is available here:
Several Java movies are available:
(These videos only deal with the case when the driving
current is along a symmetry axis (theta=0). The case
with variable theta will hopefully be updated soon)
Return to main page. 



