Flux Behavior in the Bose Glass Regime near the Mott Transition
We present molecular dynamics simulations of superconducting vortices
interacting with columnar pinning sites as an external field is
quasi-statically swept through the commensurate field B_{phi}.
We analyze the local flux profile and magnetization and find a sharp
transition in the flux profile as the local flux density passes B_{phi}
when the vortices pass from the strong pinning at individual pinning sites
to a weaker interstitial pinning. We also analyze the
voltage fluctuations and coordination number as functions of H
which characterizes the change over from strong to weak
pinning regimes.
Cross-platform QuickTime vortex movies.
- Sample with strong pinning (interstitial flow)
- Defect sites are indicated by open circles, vortices are shown as
filled dots, and the paths followed by the vortices are indicated
by lines. As the magnetic field outside the sample is increased,
vortices enter the sample from the left edge of the frame. The
vortices follow interstitial paths which move around regions with
flux lines that are strongly pinned at defects.
- Intermediate pinning strength movie
- The weaker pinning in this sample produces a different manner of
vortex transport. Pin-to-pin vortex motion, as well as interstitial
motion, is possible and the previously narrow vortex trails become
considerably broader.
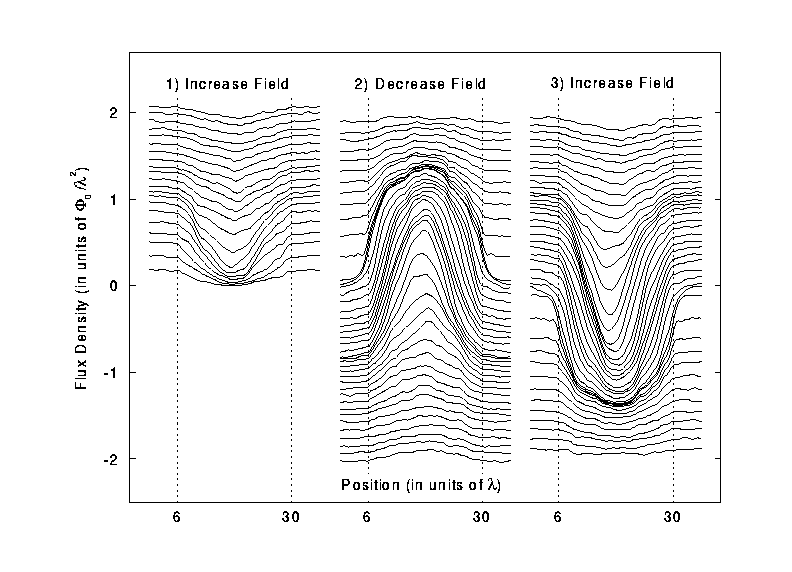
Fig. 1 - Magnetic flux density profiles. Here,
B_[\phi]=1.0. For the initial rampup phase in (1), a total of 2600 vortices
are added so the external field is 2.0. In (2), the field is ramped down and
reversed to a final value of -2.0. Finally, in (3), the field is brought back
up to 2.0. A large gradient in B can be seen for |B|<B_{\phi}.
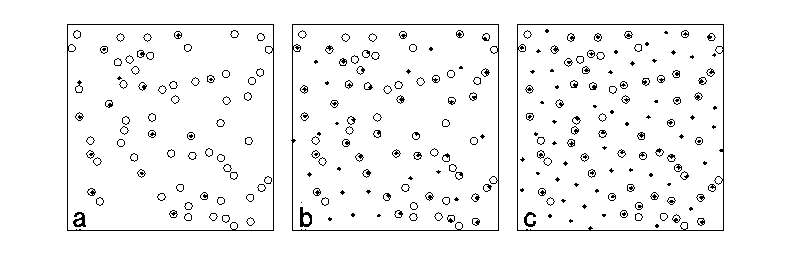
Fig. 2 - An x8 region of a 24*36 sample studied in Fig.
1. The vortices enter the left edge of each frame (which corresponds to the
sample edge. Panels A, B, and C correspond to B/B_{phi}=.31 and 1.6
respectively, of the ramp-up phase in Fig. 1. Pinning sites are indicated by
open circles, while vortices are shown as filled dots.
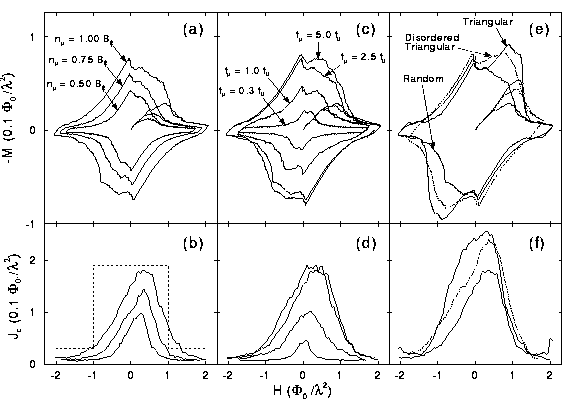
Fig. 3 - Magnetization loops (top panels) and the
corresponding critical currents (bottom panels) for several samples. The
J(B)'s are taken directly from the B(x) during the "ramp-down" (e.g., stage
(2) in Fig. 1). In (a,b), f_{p} is held fixed at 2.5 and the density of
pinning sites n is varied: B_{phi}=0.5, 0.75, 1.0. In (c,d), n remains fixed,
(B_{phi}=1.0) and the pinning strength f_p remains changed. In (e,f),
B_{phi}=1.0, f_p=2.5, and the location of the pinning sites is varied. (f)
shows the significant enhancement of J(B) that results from defects placed in
a regular triangular array, as opposed to random placement. The results show
that even a distorted triangular array of pinning sites significantly enhances
J(B) over the case with a random location of sites.
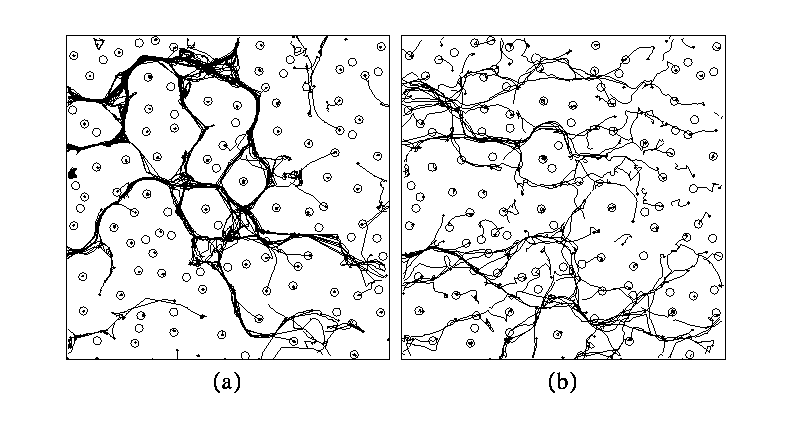
Fig. 4 - (a,b) show the trajectories of vortices while
the external field is raised from 0.95 to 1.4. (a) A x10 region of the sample
used in Fig. 1. The strength of the pinning force is 2.5 for the strong
pinning case (a), and 0.3, for the weak pinning case (b). In (a), the vortex
transport is characterized by vortex trails of interstitial vortices which
move around regions with flux lines that are strongly pinned at defects. In
(b), vortex transport proceeds in a different manner: pin/to pin vortex motion
is possible, the previously narrow vortex trails become considerably
broader.
C. Reichhardt, C. J. Olson, J. Groth, Stuart Field, and Franco Nori.
Published in Phys. Rev. B 53, R8898 (1996)
(Rapid Communications)
A copy of the paper is available here.
Go to QuickTime movie page
Return to main page.
Created by: Jared Groth and Bartholomew Hsu
Last modified: 1/5/97



