|

| Where: | |
| n | number of nodes on inductor: 1/2, 2/2, 3/2, ... |
| <turns> | number of turns in full-wave inductor |
| <area> | area of each turn (meters2) |
| H | height of full-wave inductor (meters) |
| C | Capacitance (farads) |
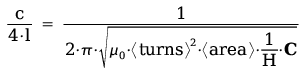
| Where: | |
| length of wire in 1/4-wave inductor |
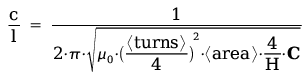
| Where: | |
| length of wire in full-wave inductor |
| 1/4 | at one wavelength |
| 1/8 | at two wavelengths |
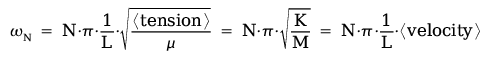
| Where: | |
| N | number of nodes on rope; 1,2,3... |
| L | total length of rope |
| <tension> | tension on rope |
| μ | linear mass density of rope |
| K | spring constant of rope |
| M | total mass of rope |
| <velocity> | wave velocity along rope |