
|

|
The classical hydrodynamic instability theories of Landau and Rayleigh-Taylor,
used in conjunction with a model of the early growth of spherical vapor bubbles
developed by the authors, predict that the early growth should be stable.
These theories do not consider the effects of heat transfer at the interface,
which is believed responsible for the observed instability of the evaporating
surface. This was confirmed by the mechanisms proposed by Prosperetti and
Plesset which, although including the effects of heat transfer, required that
the unperturbed liquid temperature distribution be known at the moment of onset
of the instability. This is generally unknown, so that no comparisons with
experiments were possible up to this point. The present pool boiling experiments
conducted in microgravity, some of which result in the explosive vapor bubble
growth referred to, permit the precise determination of the unperturbed liquid
temperature distribution using a model of the early vapor bubble growth along
with the measurement of heater surface temperature at nucleation. The limited
results to date provide good agreement with the mechanisms proposed by
Prosperetti and Plesset.

As is well known, conventional growing vapor bubbles have a smooth interface. However, under certain conditions with pool boiling in microgravity, the interface took on a rough appearance, accompanied by rapid growth rates. Figure 2 shows a typical roughened hemispherical vapor bubble 17.5 milliseconds after nucleation. This type of roughened surface has not been observed with boiling in earth gravity, most likely due to natural convection.
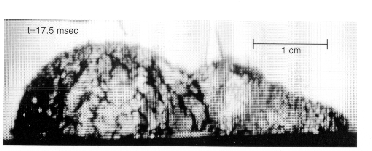
Two typical growth sequences are presented in the Figure 3 together with the operating conditions. The differences in the wall superheats at nucleation are particularly noteworthy, and are associated with the dramatic differences in the growth rates, especially obvious by comparing the bubble sizes at 7.5 milliseconds. It is of interest that the very first picture A in in the figure below already exhibits a roughened surface, which implies that the onset of the interfacial instability is somewhere between 0 ~ 2.5 milliseconds. It is also to be noted that the bulk liquid is slightly subcooled in Figure 3(a) and considerably subcooled in Figure 3(b).

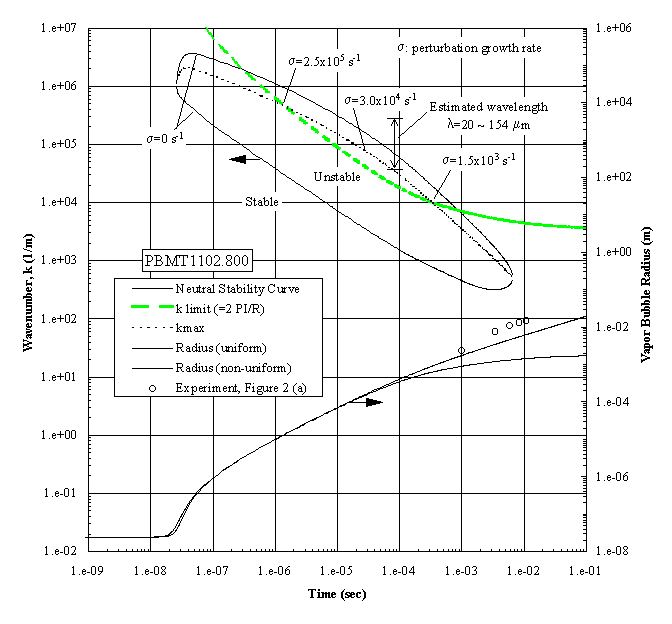
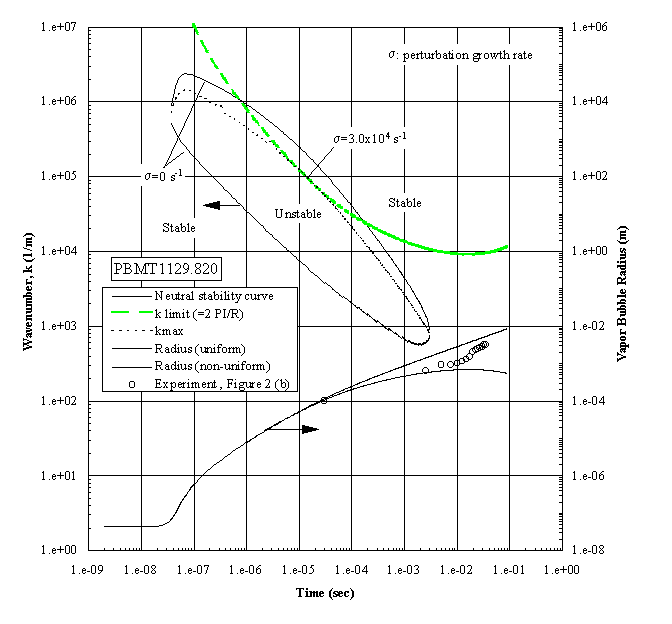
The growing bubble radius is included, together with the corresponding measurements, all of which have unstable interfaces, as shown in Figure 3(a). The apparent unstable regime exists over a wide interval of time. However, a constraint must be imposed within this regime in that the wavelength cannot exceed the bubble diameter. This is called the ‘k limit’, defined as , for practical reasons as discussed previously by Sturtevant and Shepherd (1982), and is included in Figure 4. The "most unstable regime" is determined by the intersections between the ‘k limit curve’ and the maximum wavenumber curve, giving a range of times between 1.2x10-6 and 3.0x10-4 seconds as the interval of instability. The radii measurements indicated are beyond this interval, demonstrating that the onset of the instability occurred earlier. The corresponding computations were carried out for the case shown in the Figure 3(b), which demonstrated a distinctive stable bubble growth, and the results are presented in Figure 5. The conditions required for the "most unstable regime" are satisfied only marginally, which indicates that the probability for instability will be low, considering that the ‘ k limit’ curve is the lower bound. The result is in fair agreement with the measurements, in which the measured bubble radii are between the computational limits.
The occurrence of extremely rapid evaporation at a vapor bubble interface has been demonstrated with superheats far below the superheat limit. This occurred with pool boiling in a microgravity environment, and is attributed to the growth of an interfacial instability. Such a process can produce an abrupt pressure rise and be quite destructive if a sufficiently large surface area is present.
Sources of perturbation growth other than an instability can arise at the liquid-vapor interface of a bubble. The present plane instability model including heat transfer reasonably predicts not only the occurrence of explosive bubble growth, but also the wavelength of the unstable interface. Local heat transfer at the interface is an essential mechanism to the instability, where the heat transfer increases at a trough while it decreases at the crest, which can produce differential vapor recoil. This can lead to the distortion of the crests such that liquid particles become entrained with the vapor, departing the interface, and which can then serve to further increase the evaporative flux.

For questions or comments, email pfahey@engin.umich.edu