by
Larry
"Harris" Taylor, Ph.D
This is an electronic reprint and expansion of an article that appeared in Sources (July/August, 1992, 49-52.) This material is copyrighted and all rights retained by the author. This article is made available as a service to the diving community by the author and may be distributed for any non-commercial or Not-For-Profit use.
All
Rights Reserved.
Go To: Home About "Harris" Articles Slides War Stories Editorials Links Fini
Jump To: Kinetic Absolute Values Charles Guy-Lussac Boyle General Dalton Henry Real VanDer Waal
The behavior of gases in the physical world is a major influence on the diver. Since the changes in gas volume related to pressure and temperature effects buoyancy, as well as the amount of breathing gas available to the diver, understanding some basic principles of gas characteristics can dramatically increase diver comfort and safety.
All
gases, irrespective of chemical composition, demonstrate similar behavior in
response to physical changes of composition, temperature, and pressure. This
uniformity of physical behavior was of great interest to early scientists. It is
one of the dogmas of science that the behavior of a material is a reflection of
the particles that make up the substance. In other words, the differences between a solid,
liquid, and gas reflect the movement of the small particles (atoms) that compose
all matter. This assumption is part of the Kinetic Theory Of Gases (Kinetic is
from the Greek word for motion). Historically, the description of gas properties has been summarized by
the mathematical equations describing the relationships between gas volume,
pressure and temperature. These equations, named after the scientist who first
demonstrated their validity, have been labeled the "gas laws." These gas
laws are best understood within the framework described as the kinetic theory of
gases:
1. Gases are composed of molecules.
2. These molecules are in constant motion. This is why gases mix to
uniformity and fill all portions of the containment vessel.
3. Molecules of a gas collide frequently with each other and with the walls of the containment vessel.
4. Under ordinary circumstances, the distance between gas molecules is far greater than the size of the individual molecules. This is why gases can be compressed.
5. The molecules of a gas move in all directions with an average velocity at a given temperature. At a given temperature, the average energy of molecules in the gaseous state is the same for all substances.6. Molecules are perfectly elastic; thus they lose no energy when they collide with another molecule. (If they lost energy on collision, the temperature of a gas mix would always decrease with time.)
These six assumptions are the basis for understanding gas behavior. For example, the measurement of the "intensity" (force per unit area) of the collisions of the gas molecules with the walls of the containment vessel is termed pressure. As we increase the kinetic energy (by raising temperature) the molecules will have more velocity and will collide with more force more often on the vessel walls. This is why pressure increases in a closed container as temperature is raised.
One way of conceptualizing this is to think of gas molecules like little metal pellets (bb's). As they move about in containment, they will strike the walls of the container. In the illustration below, these gas "pellets" are randomly moving inside a cylinder. At the right end of the cylinder in the illustration is a piston, held in place by some spring mechanism within the brown box. As the gas molecules strike the flat plate of the piston, the combined force of all the impacts will move the piston backwards until the force of the gas molecules (bb's) striking the flat plate of the piston balances a spring device contained within the brown box. A measurement of this impact is displayed on a mechanical gauge. If we increase the temperature, we increase the average velocity of the gas molecules. This means they will strike the flat plate faster (with more force) and the plate will move within the cylinder to indicate a higher pressure.
GAS LAW FUNDAMENTALS
The relationship between temperature, pressure, and volume has been extensively studied. Historically, the behavior of gases was evaluated by measuring the temperature, pressure and volume of the material under study. Because of the complexity of attempting to simultaneously measure and predict all values, typically, one of the values (P (Pressure) , V (Volume) or T (Temperature) ) was held constant. Then another value was changed to determine that change on the third parameter.. For example, an experimenter would hold pressure constant (stay at same altitude above sea level) and measure the gas volume change (in a flexible container) as the temperature was varied. In turn, over time, all of the possible combinations were examined and each situation has been given a name for the scientist who firmly established the validity of the particular relationship that is now called a gas law. Association of scientist's name with the mathematical relationship describing gas behavior under some set of specified conditions is one way of remembering these gas laws.
The magnitude or behavior of gases is best illustrated by looking at some numerical examples. It is important to remember that in all gas law problems, the relationships are valid only when ABSOLUTE UNITS for pressure and temperature are used. In other words, to make the equation describe reality, absolute values must be used. Absolute temperature was originally defined when the linear relationship between temperature and volume was discovered (See Charles Law, below). So, not using absolute temperature most likely means you are not in a range where the relationship between temperature and volume is linear and any solution will be incorrect.
Since we live under a gaseous blanket (and this gas has weight and thus exerts a force called pressure), the weight of this volume must be considered because gases behave according to the TOTAL pressure acting on them. We typically label our pressure gauges 0 because for many applications (measuring pressure within a container) we are NOT CONCERNED with the behavior of gases; we simply want to know if the pressure measure on the gauge is less than the tolerated pressure (to prevent an explosion) of the container or, as in scuba diving, we use the pressure gauge as a measure of remaining gas (see Estimating Gas Consumption).. However, when we choose to examine or predict the behavior of gases, we MUST consider all the forces involved. So, absolute pressure is defined as the pressure we measure (on the gauge) plus the pressure exerted from the weight of the atmosphere. This takes the form of this equation:
Pa = Pg + P atm where
|
Pa = Absolute pressure |
|
Pg = Gauge pressure |
|
Patm = Atmospheric pressure |
All of these measurements must be in the same units. Typically, in diving, we use atmospheres as a measure of pressure because this makes the pressure of the atmosphere defined as 1.0. Thus, when using atmospheres, the above equation becomes
Pa = Pg + 1.0
It is very important that measurements be in the same units. Mixing units (gauge pressure in psi or bar and atmospheric pressure as 1) will lead to the wrong numerical value for your solution. One of the most common sources of error is NOT USING absolute pressure and temperature values. So, get into the habit of converting to absolute units whenever you enter the realm of solving gas related problems. Finally, when the weight of the atmosphere changes (as in going to altitude where there is less overhead weight of the atmosphere) the numerical value for P atm will change (See Altitude Arithmetic ).
NOTE: It makes no difference if the units of pressure are expressed in psi, mm Hg, cm H2O, bars, kilopascals, g/sq cm, kg/sq m, etc. However, it is necessary to use absolute measurements and to keep the units the same in both starting and ending conditions being considered.
The French scientist, Jacques Charles, in 1787, studied the relationship between temperature and volume at constant pressure. This study was prompted by an attempt to understand how hot air balloons worked. He noted that in the vicinity of zero degrees Celsius, the volume of a gas decreased by a factor of 1/273 for each degree Celsius decrease. If one theoretically continued this decrease in temperature, then a gas would have zero volume at -273 degrees C. This value is termed Absolute Zero. (If a gas has zero volume, then there will be no molecular motion (velocity = zero in the kinetic energy equation) and thus no kinetic energy). Measurements of temperature based on this absolute zero point are termed Absolute Temperature. (Since gases will liquefy before absolute zero is reached, the "zero volume" state is not obtainable.) Since this 1/273 change in volume corresponds to one degree change on the absolute temperature scale, absolute temperatures are used when using "the gas laws" described below to predict variations in pressure, temperature, and volume. Charles' observations have been formalized into Charles' Law:
The volume of a gas at constant pressure is directly proportional to the absolute temperature.
A practical example of Charles law involves the effect on the volume (size) of any flexible container with change in temperature. Inner tunes, surface floats, etc. will increase in volume when heated and decrease in volume when chilled. So will the volume of gas in a buoyancy compensator when passing through thermoclines. So, the effect of buoyancy from slight changes in pressure when moving through water column zones with dramatically different temperatures will be exacerbated by this temperature effect on volume. Thus, as the gas chills after entering a thermocline, buoyancy will continue to decrease until the temperature of the gas in the bc is the same temperature as the ambient water. Likewise, on ascent out of the thermocline, the movement into warmer water will cause an increase in buoyancy from the expansion of the gas in the bc related to this temperature effect.
ENGLISH
EXAMPLE: If a scuba cylinder is capable of delivering 40 ft3 of air to a
diver at 78 oF, how much air is available at 55 oF?
ANSWER: Using Charles' Law
First, determine absolute temperature (T) at the two conditions (1 and 2) being considered:
T1 = 78 oF + 460 = 538 oR
T2 = 55 oF + 460 = 515 oR
NOTE: The subscripts are mathematical conventions for keeping track of conditions. The small one and two refer to temperature, pressure or volume in the first case considered or the second case considered, It is generally NOT important which set of situations is one or two. What is important is that all three variables (T, P, or V) for the same set of conditions have the same subscript.
Charles
Law:
V1 / T1
= V2
/ T2
|
V = Volume at conditions 1 and 2 |
|
T = Absolute temperature at conditions 1 and 2 |
Substituting:
40 ft3
/ 538 oR
= V2
/ 515 oR
Solving:
V2
= 38.3 ft3
COMMENT:
The temperature 55 oF is typically the temperature of the first thermocline of a
fresh water lake. Charles' law explains why divers have less air available to
them in colder water.
METRIC
EXAMPLE: A scuba cylinder is capable of delivering 1000 l of air at 25 oC.
If this cylinder is used at 18 oC. how much air will be available to
the diver?
ANSWER:
Using Charles' Law:
V1 / T1 = V2 / T2
Determine absolute temperature:
T1 = 25 oC + 273 = 298 K
T2 = 18 oC + 273 = 291 K
NOTE:
By international convention, there is no degree symbol used for temperature
defined on the Kelvin scale.
Substituting:
1000 l / 298 K = V2 / 291 K
Solving
V2 = 976.5 l
COMMENT:
This demonstrates a reduction in available air to the diver if the gas in the
cylinder is cooled.
In 1699, French physicist Guillaume Amontons developed a device for measuring temperature based on the change in gas pressure with temperature. He used this thermometer to point out that water always boiled at the same temperature. He also measured (in a non-rigorous way) increase/decrease in gas pressure with temperature. For some reason, his work was ignored by the scientific community and references to him are minimal. Within the scientific community, the relationship between pressure and temperature has been associated with the French scientist, Joseph Guy-Lussac. Since Guy-Lussac collaborated with Jacques Charles, some have associated this principle with Charles. However, Charles, the mentor, gave credit for this relationship to his student, Guy-Lussac, because Guy Lussac was the first to build an apparatus to demonstrate the validity of the linear mathematical relationship between pressure and temperature at a constant volume. In science and technology, credit is generally assigned for "reduction to practice" and since Guy Lussac built the apparatus to demonstrate the validity of this law, it is appropriate to give him the credit. The bottom line, however: is that the principle, not the name, is important to you as a diver! Use whatever name is easiest to remember.
Near the turn of the 19th century, Guy-Lussac investigated the relationship between pressure and temperature while the volume was held constant. He did his measurements using a fixed volume, gas filled sphere. He measured the temperature and pressure of the gas in the sphere while ascending in a hot air balloon. His published observation (known as Guy-Lussac's Law) states:
The pressure of a gas at constant volume is directly proportional to the absolute temperature.

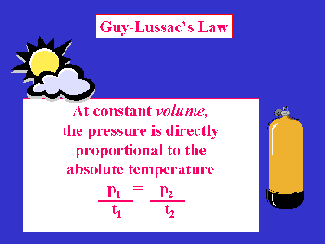
ENGLISH EXAMPLE: A scuba cylinder contains 3000 psig (3014.7 psia) at 78 oF. It is left in the trunk of a car on a hot summer day. If the temperature of the trunk is 115 oF, what will be the gauge pressure of the cylinder?
ANSWER: Using Guy-Lussac's Law (Remember absolute temperature and pressure)
P1 / T1 = P2 / T2 where
|
P = Absolute pressure at conditions 1 and 2 |
|
T = Absolute temperature at conditions 1 and 2 |
First, Determine absolute temperature
T1
= 78 oF + 460
= 538 oR
T2 = 115 oF + 460 = 575 oR
Substituting into Guy-Lussac's Law
3014.7 psia / 538 oR = P2 / 575 oR
Solving:
P2 = 3222 psia
Converting to gauge pressure (gauge reads zero when absolute pressure is one)
3222 psia - 14.7 psi = 3207.3 psig
COMMENT: There is an increase in pressure associated with heating a scuba cylinder. To prevent this increase in pressure (and possible rupture of the safety disc), it is especially important to store full scuba cylinders in a cool place.
METRIC EXAMPLE: A cylinder at 25 oC (298 K) contains gas at a gauge pressure of 200 bar (201.01 bar absolute). Predict the pressure at 42 oC (315 K).
ANSWER:
Using Guy-Lussac's Law (Remember Absolute Temperature and Pressure)
Substituting:
201 bar / 298 K = P2 / 315 K
Solving:
P2 = 212.5 bar
Converting
to gauge pressure:
P2
= 212.5 bar - 1.01 bar
P2 = 211.5 bar
Thus,
a scuba cylinder with a gauge pressure of 200 bar at 25 oC heated to 42
oC will
show a gauge pressure of about 212 bar.
NOTE: A scuba cylinder is a constant volume device. As kinetic energy increases with temperature, the molecules travel faster. They hit the vessel walls harder and more often. This means pressure, NOT volume, within the cylinder increases as the temperature is raised
In
1660, Sir Robert Boyle published the classic "The Spring Of Air And Its
Effects" in which he measured the relationship between pressure and volume
at constant temperature. He measured the volume of air trapped at the small end
of a J-shaped tube. The tube was filled with mercury and the volume of the air
space was measured. Adding mercury, (increasing the height of mercury in the
J-tube) decreased the volume of air trapped at the small end of the J-shaped
tube. He noted that the product of the pressure (as determined by the height of
the mercury column) and the volume was constant.
Expressed mathematically:
P V = k where
|
P =
Absolute pressure
(height of mercury in tube) |
|
V =
Volume (of air
space in tube) |
|
k =
Constant |
This
relationship, PV = k, held for a variety of P, V combinations. In mathematics,
products equal to the same value can be set equal to each other. This gives us
Boyle's Law:
|
P = Absolute pressure at conditions 1 and 2 |
|
V = Volume at conditions 1 and 2 |
Boyles' Law states
The volume of a gas at constant temperature, varies inversely with the pressure.
A corollary to this law states that density (mass/volume) increases directly with the pressure.

ENGLISH EXAMPLE: What is the physical volume (in cubic feet) of an aluminum "80" scuba cylinder?
ANSWER: An aluminum 80 delivers 80 cubic feet of air at one atmosphere (14.7 psia) when filled to a pressure of 3000 psig (3014.7 psia). Thus, the physical volume of the tank will be the volume at 3000 psig (3014.7 psia)
Substituting into Boyle's Law:
Solving
for V2:
V2 = 0.39 ft3
This
physical volume represents how much water the cylinder would hold if the valve
were removed and the cylinder were filled with water. This is the value that
Europeans refer to as the "water capacity" of a scuba cylinder.
NOTE: Scuba divers carry a small physical volume on their back (0.39 cubic feet, in this case), but have large volumes of available, breathable air (80 cubic feet at sea level) because the air is stored at high pressure and released at ambient pressure by a mechanical device, the regulator.
METRIC EXAMPLE: A scuba cylinder is rated at 2400 l with a pressure of 200 bar. What is the physical volume (water capacity) of the cylinder.
ANSWER:
The cylinder delivers 2400 l if all the air is released at 1 bar. The physical
volume (water capacity) of the cylinder is the volume of gas compressed to 200
bar. The volume can be found by using Boyle's law:
P1 V1 = P2 V2
Determine absolute pressure: gauge + atmospheric
200 bar + 1 bar = 201 bar
Substituting into Boyle's law
:
P1 V1 = P2 V2
(1 bar) x (2400 l) = (201 bar) V2
Solving:
V2 = 11.9 l
ENGLISH EXAMPLE: A scuba cylinder has a rated capacity of 80 ft3 on the surface. Determine the volume of air from this cylinder that will be available to the diver at 33, 66, 99 and 132 fsw.
ANSWER:
Boyle's law allows calculation of decreasing volume of air with increasing
depth.
Determine
absolute pressure: (Hydrostatic pressure + Atmospheric pressure):
For 33 feet
33 fsw x 33 fsw/atm = 1 atm
1 atm + 1 atm = 2 ata (ata = absolute pressure in units of atmospheres)
For 66 feet:
66 fsw x 33 fsw/atm = 2 atm
2
atm + 1 atm = 3 ata
For 99 feet:
99 fsw x 33 fsw/atm = 3 atm
3
atm + 1 atm = 4 ata
For 132 feet:
132 feet x 33 fsw/atm = 4 atm
4 atm + 1 atm = 5 ata
Substituting into Boyle's Law:
P1 V1 = P2 V2
For 33 fsw:
(1 ata)(80 ft3) = (2 ata) V2
V2
= 40 ft3
For 66 fsw:
(1 ata)(80 ft3) = (3 ata) V2
V2 = 26.7 ft3
For 99 fsw
(1 ata)(80 ft3) = (4 ata) V2
V2 = 20 ft3
For 132 feet:
(1 ata)(80 ft3) = (5 ata) V2
V2 = 16 ft3
The answers are summarized in the following table:

The volume shown is the volume calculated for a 80 ft3 cylinder. The fraction represents the proportional amount of the surface volume at that absolute pressure available from ANY size scuba cylinder. The % change represents the difference in volume between each successive 1 ata pressure change.
METRIC EXAMPLE: The corresponding Metric Table for a 2000 liter cylinder:

The
volume shown is the volume calculated for a 2000 liter cylinder. The fraction
represents the proportional amount of the surface volume at that absolute
pressure available from ANY size scuba cylinder. The % change represents the
difference in volume between each successive 1 bar pressure change.
Remember
- as pressure increases, volume decreases. Since breathing is basically a
constant volume operation, this is the equivalent of saying that the deeper you go,
the less breathing gas will be available to you and thus, the sooner you will consume the
air contained in your scuba cylinder. (See Estimating
Gas Consumption
) Likewise,
as pressure decreases (as on ascent on scuba), the volume of gas in the lungs
and other air spaces will increase. Since the physical size of the body cavity
(lungs. ears, sinus, etc.) containing the air is limited, the volume of
expanding gas either properly vents through open unobstructed passages or
increases by damaging or rupturing tissue. (Analogous to increasing the size of a
chewing gum bubble by exhaling into it until it bursts.). As the table clearly
shows, the greatest volume change per unit of pressure is in the vicinity of the
surface. This means the most risk of a pressure-volume type injury
("Squeezes" and barotraumas) is near the surface.
Any
two of the three gas laws of Boyle, Charles or Guy-Lussac can be combined into a
relationship termed the General or Combined Gas Law:
( P1
V1
)
/
T1
= (P2
V2 )
/
T2
This relationship can be used to predict pressure, volume, and temperature relationships where any five of the six variables are known.
ENGLISH
EXAMPLE: The gas in a scuba cylinder occupies a volume of 72 ft3
at 78 oF on the surface. What volume of gas is available to
the diver at a depth of 126 ffw and a temperature of 40 oF?
ANSWER:
Determine pressure:
On the surface:
P1 = 1 ata
At 126 ffw
: P2 = 126 ffw x 1 atm /34 ffw = 3.7 atm
(In fresh water; 34 ffw = 1 atm)
3.7 atm + 1 atm = 4.7 ata
P2 = 4.7 ata
Determine
absolute temperature:
T1
= 78 oF + 460 =
538 oR
T2
= 40 oF + 460 =
500 oR
General
Gas Law:
( P1 V1 ) / T1 = (P2 V2 ) / T2
Substituting:
Solving:
V2 = 14.2 ft3
This demonstrates the decrease in available breathing gas volume associated with descent to deep, cold fresh water that might be encountered in the Great Lakes of the United States.
METRIC EXAMPLE: Calculate the volume of gas available to a diver when a cylinder having a volume of 2000 l with a gauge pressure reading of 200 bar at 25 oC (298K) is used at a depth of 20 msw (3 bar) and a temperature of 30 oC (303K).
ANSWER:
Substituting into General Gas Law:
(1 bar) (2000 l) / 298 K = (3 bar) V2 / 303 K
Solving:
V2 = 678 l
Since
it is most likely that both temperature and resultant pressure will vary between
the filling of a scuba cylinder and its use, the General Gas Law will give a
slightly more realistic evaluation of volume available at depth than a
relationship that only examines two of the three pressure- temperature-volume
variables.
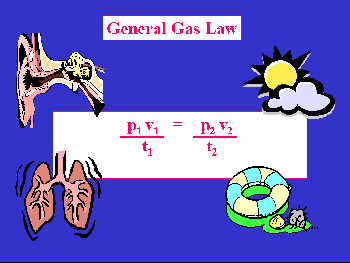
The English chemist John Dalton with collaborator William Henry (of Henry's Law) observed in 1810 the pressures obtained when gases were mixed n the same container. He concluded that when gases were mixed in a container, each gas behaved as if it were the only gas present. Thus, the total pressure in a closed system can be obtained by summing the pressures of each individual component. The pressure of each individual component is termed the partial pressure. Expressed mathematically:
p(total) = p1 + p2 + p3 + .pn
where n = maximum number of components in the gas mixture
.
The total pressure of a gas mixture is the sum of the partial pressures of all the components.
Since the distances between gas molecules are so vast, each gas molecule behaves as if it were alone. So, even though components being mixed have pressures of their own, when combined in a container at near atmospheric pressures, the total pressure will be simply the sum of the individual components. However, under high pressure, the volume of gas molecules, compared to the total volume of space available, become significant and this simple summing of pressures no longer applies.


Again, this concept is best illustrated with numerical examples.
EXAMPLE: A one cubic foot (28.3 l) container contains 500 psig (34 bar) of nitrogen gas. Into the container, an additional 346 psig (23.8 bar) of oxygen gas is introduced. Determine the final pressure.
ANSWER:
Using Dalton's Law:
p(total) = p1 + p2
Substituting:
p(total) = 500 psi + 346 psi
METRIC:
p(total)
= 34 bar + 23.8 bar
Solving:
ENGLISH:
p(total) = 846 psi
METRIC:
p(total) = 57.8 bar
Another way of viewing Dalton's Law
pn = P(total) x fraction gas(n) by volume
EXAMPLE: Determine the partial pressure of oxygen in compressed air at a depth of 88 fsw (26.8 msw)
ANSWER:
Using Dalton's Law
pn = P(total) x fraction gas(n) by volume
Remembering
that Air = 21 % O2
Determine absolute pressure
ENGLISH:
P (Hydrostatic) = 88
fsw x 1 atm / 33 fsw
METRIC:
P (Hydrostatic) = 26.8 msw x 1
atm / 10.1 msw
P (absolute) = 2.7 atm + 1 atm = 3.7 ata
Substituting:
p O2 = 0.77 ata
EXAMPLE: Determine the partial pressure of nitrogen (78% of air) at the same depth.
p
N2 = 3.7 ata x 0.78
p N2 = 2.89 ata
NOTE: The large partial pressure of nitrogen at depth is one of the reasons for the accumulation of nitrogen within the diver. Since nitrogen is physiologically inert (not consumed by metabolism), this nitrogen accumulation can be detrimental to the diver.
Whenever a gas is in contact with a liquid, gas will dissolve in the
liquid. There is a continual movement of gas molecules which are simultaneously
moving out of solution into the gas phase and moving from the gas phase into
solution within the liquid phase. Although it is impossible to predict the
behavior of an individual gas molecule, the net movement of gas will equilibrate
such that the partial pressure of the gas going into solution is the same as the
partial pressure of the gas coming out of solution. When the gas reaches the
state where the amount of gas going into solution is the same as the amount of
gas molecules coming out of solution, the solution is said to be saturated with
gas. This state is termed equilibrium. At this point, although individual gas
molecules will move at random into and out of solution, there will be no net
change in gas concentration within the solution.
Henry's Law states
The amount of gas that will dissolve into a solution is directly proportional to the partial pressure of that gas and inversely proportional to the absolute temperature.
The greater the partial
pressure of the gas, the greater the driving force for solution and the greater
the amount of gas that will dissolve into solution. As the temperature
decreases, more gas will dissolve into solution. It is very important to realize
that Henry's law is concerned with the amount of gas in solution when
equilibrium is reached. It specifically does not address how rapidly that state
is reached!
The dissolution of nitrogen within body tissues is approximated by
Henry's Law. The deeper one dives, the greater the partial pressure of nitrogen
(and any gas in the gas mix) and the greater the gas load each tissue must bear.
Upon ascent, the partial pressure in the gas phase decreases. The gas in
solution will then escape from solution in an attempt to obtain equilibrium. If
this escape from tissue is too rapid for the body to handle, decompression
sickness is the result. This is discussed in more detail in the physiology and
decompression chapters of this text.


An adiabatic system is one in which no heat is added or removed. For an ideal gas (See section on Real vs. Ideal) the following relationship:
Cv ln ( T2 / T1 ) = -R ln (V2 / V1) where
| Cv = Heat capacity at constant volume |
| ln = Natural logarithm |
| T = Absolute temperatures at condition one or two |
| R = Universal Gas Constant (see below) |
| V = Volume |
Thi This equation can be used to calculate the temperature change following an adiabatic change in volume. The mathematics indicates an increase in temperature during compression and a decrease in temperature on expansion of an ideal gas. Thus, the diver notices the scuba cylinder gets hot when filled (The air has been compressed, has less volume, so temperature goes up.) This increase in temperature can be substantial, as much as 1500 oF during rapid compressions. In the presence of hydrocarbon (greases and most lubricants) contaminants, this heat can serve as an energy source for fire and/or explosion in an oxygen enriched atmosphere. When air is rapidly released from a scuba cylinder, either from directly opening the valve to release its contents prior to inspection or by using the purge valve, the volume of the gas increases, so temperature must go down. (The adiabatic cooling associated with gas movement driven by high pressure through a tiny orifice is called the Joule-Thompson effect.) Likewise, as offshore wind moves up a mountain slope, it expands from the decrease in pressure, and cools. Eventually, the cooling will result in the temperature falling below the dew point and clouds or fog then form.
ADDITIONAL TOPICS RELATED TO GASES
The following discussion on real and ideal gas laws is beyond the scope
of recreational diving. The differences between real and ideal gas behavior is,
for the most part, insignificant for the diver using compressed air within the
traditional recreational diving standards. However, these differences can be
substantial when using gas mixtures different from air. Since some within the
recreational diving community are beginning to explore the realm of breathing
mixes other than air. For that reason, this expanded discussion of real and
ideal gas behavior is furnished as a reference.
EXPANDING ON BOYLE: THE REAL GAS LAW
Remember that Boyle measured the product of pressure and volume and
always got the same number:
PV
= k
Scientists wanted a single equation that would, without having to measure
multiple volumes, temperatures, and pressures give reliable pressure,
temperature, volume, AND quantity measurements on gases. This led to an
investigation of this constant k. It turns out that temperature and the quantity
of a gas can be added to this equation. This new generalized gas equation takes
the form:
PV = nRT where
|
P = Absolute pressure |
|
V- Volume |
|
n = Number of moles present |
|
R = Universal Gas Constant (see below) |
T = AbsT = Absolute temperatures at condition one or two |
A Mole is a chemical measurement of quantity. It is used to relate compounds of different molecular weights. One mole (a mass equal to M grams, where M is the molecular weight of a substance) contains Avagadros' Number (6.024 x 1023) of molecules. For example: one mole of O2 (molecular weight of 32) is 32 grams; this mole of oxygen contains the same number of atoms as 28 grams, one mole, of N2 (molecular weight of 28). Chemists use moles because physical and chemical properties are determined by the numbers of molecules present. Using moles allows chemists to compare substances that have different molecular weights and densities. The mole is also important because it turns out that one mole (the molecular weight (MW) of a gas expressed in grams) at so-called standard temperature and pressure (STP; 0 oC, 1 atm absolute) always has the same volume, 22.414 liters. Thus, using this equation, it is possible to derive not only pressure, temperature, and volume relationships, but quantities of a substance as well.
R is the "universal gas constant" - i.e., it's a number that has been placed into the equation so that the numbers calculated are similar to the numbers observed. (A common trick in science is to add "constants", or fudge factors, to make equations reflect observed reality.) R has been determined from numerous physical measurements. It is equal to the value of PV/nT. (Note: the numeric value of R will vary dependent on the units chosen to measure pressure, volume, and temperature.)
EXAMPLE:
How many liters would 5 moles of any gas occupy at 25 oC (298 K) and 2 atm
absolute pressure.
ANSWER: Using:
PV = nRT; R = 0.082 l-ata
Substituting:
(2
ata) V = (5 moles) (0.082 l-ata
) (298 K)
Solving:
V =
61.1 l
This, 5 moles of gas would correspond to:
5 moles x 32 g / mole = 160 g O2 (Oxygen, MW = 32)
5 moles x 28 g / mole = 140 g N2 (Nitrogen,
MW = 28)
5 moles x 4 g / mole = 20 g He (Helium, MW = 4)
NOTE: 20 g of He occupies the same volume as 160 g of O2. This is because 20 g of Helium (5 moles) contains the same number of molecules as 160 g (5 moles) of Oxygen. This is why moles, not grams (or any other mass units), are used in chemical equations.
EXAMPLE:
Predict the volume of one mole of gas at 5.1 ata and 3 oC (276 K).
ANSWER: Using Ideal Gas Law
PV = nRT
Rearranging:
V = nRT / P
Substituting:
V =
(1 mole) (0.082 l-ata)
276 K
5.1
ata
V = 4.44 l
The following material is beyond the scope of most recreational diving. It does have some relevance in so-called "technical diving" where pressures and gas mixes create situations that are not reliably addressed with the simplistic linear curves of the ideal gases.
REAL & IDEAL
The equation: PV = nRT is called the ideal (or perfect) gas law. It is
used to predict the behavior of so-called Ideal Gases. An ideal (or perfect) gas
is a gas that exactly behaves according to the laws of Charles and Boyle. In
other words, for an ideal gas, the product of PV is always constant (the k in
Boyle's law is always equal to nRT) In reality, NO GAS IS IDEAL! This means the
product PV does not always remain a constant value. It turns out that most
gases, at conditions near STP (standard temperature and pressure; 0 oC, 1 ata)
behave according to Boyle's and Charles' Law. As temperature and pressure move
away from STP, values calculated by the ideal gas laws, including Boyle's and
Charles', are different from the values measured experimentally. The ideal gas
situation is best suited to high temperatures and low pressure (when the
distances between individual gas molecules is the greatest, so molecular volume
is insignificant compared to the container volume).. At scuba cylinder pressures,
gases no longer are ideal and as such, ideal equations no longer accurately
predict volume and pressure measurements. This deviation from ideal behavior has
been explained by the fact that molecules do occupy space. ( An ideal gas
molecule occupies zero volume.) Since moving molecules cannot freely move
unhindered in all directions, the volume appears larger than predicted by ideal
behavior. Also, slight forces of attraction (Van der Waals forces) exist between
molecules so that individual molecules truly do not act totally independent of
each other. This makes the volume appear smaller than predicted for ideal
behavior.
The proximity of molecules to each other will depend on both temperature
and pressure. Low pressures and high temperatures keep molecules apart and allow
gas behavior to be close to that predicted by the Ideal equations. However, low
temperatures and high pressures (like that found in a scuba cylinder) tend to
decrease molecular distance and significant difference from Ideal behavior is
observed. Such behavior is termed real behavior and equations that predict gas
behavior in regions where the simple ideal laws are inadequate are termed real
equations.
Under ordinary conditions, the deviation between real and ideal gas behavior is of little concern to divers. However, at scuba cylinder pressures, the difference between real and ideal calculations can be substantial. This difference is particularly important when calculating components for a breathing mixture other than air.
Since measurement of the pressure and volume of a number of gases at different conditions clearly demonstrated that the simple ideal gas law was inadequate to predict observed behavior, it became necessary to "modify" the ideal gas equation. Near the end of the 19th, a Dutch chemist, Johanns Van Der Waals, examined the ideal gas equation and made the following assumptions:
1.
At low pressures, the intermolecular attractive forces act to cause a decrease
in pressure. This causes the product PV in the Ideal gas equation to be lower
than expected.
2.
At high (scuba-cylinder) pressures, the volume occupied by individual molecules
is significant with respect to the total volume occupied by the gas. (At high
pressures, the density of the gas is greater. Thus, there will be more molecules
per unit volume and the percent volume occupied by gas molecules will increase.)
Since the term V in the Ideal gas equation should represent only free space
available for gas movement, a correction would be needed to account for the
volume of space occupied by gas molecules. Since this correction factor is not
present in the Ideal gas law, values calculated for PV at high pressures are
larger than measured.
In order to make the ideal gas law more closely conform to observed parameters, Van Der Waals introduced the following modifications:
1. The ideal pressure could be represented as:
P (ideal) = P + (an2 / V2 ) where
|
P = Absolute pressure measured |
|
V = Volume |
|
a =
Constant, characteristic of each gas |
|
n =
Number of moles present |
The constant a represents the attraction between molecules; it is different for each gas and has been determined from empirical observations.
2. The ideal volume could be represented as:
P (ideal) = V -nb where
|
V
= Volume measured |
|
b =
Constant,
characteristic of each gas |
|
n =
Number of moles |
The constant b represents the excluded volume of the molecules that make up the gas; it is different for each gas and it has been determined from numerous measurements. Tables of a and b values for various gases are available. One of the most common of such data can be found in the CRC Handbook Of Chemistry And Physics. Values can also be located in almost any chemical engineering textbook. The constants a and b are for pure compounds only and values for mixtures, except air, are commonly not found.
Adding these new P & V terms to the ideal gas law gives rise to the Van Der Waals' equation for real gases. This equation has also been called the real gas law:
(P + an2)/V2
) (V
- nb) = nRT
This equation can be used to derive pressure, temperature, volume, and
REAL
VS. IDEAL CALCULATIONS
The difference between real and ideal is best illustrated by numeric example.
EXAMPLE: Determine the pressure in a scuba cylinder filled with air using both real and ideal gas laws.
ANSWER:
Assume a scuba cylinder has a volume of 0.4 cubic feet (from Boyle's Law problem
above.) This corresponds to a scuba cylinder volume of:
|
0.4 ft3 x
(12 in)3
x (2.54 cm)3 x
1
l
= 11.3 l |
| cylinder ft3 in3 1000 cm3 |
Assume this scuba cylinder contains 80 cubic feet (about 2266 l) of gas at atmospheric pressure. Since one mole of gas occupies 22.4 liters at STP, we can approximate the number of moles at STP:
2266 l
To simplify our arithmetic, we will assume a scuba cylinder contains about 100 moles of air.
We will also use 25 oC (298 K) as our temperature.
R is 0.0821 l-ata/ K mole)
IDEAL GAS LAW SOLUTION:
Using
the Ideal Equation:
PV
= nRT
Rearranging:
P = nRT / V
Substituting:
P
= (100 moles) (0.0821 l-ata/deg K moles) (298 K)
11.3 l
P = 216.5 ata (This corresponds to 3182.5 psia or 3168 psig)
Now, let's compare this to the pressure
predicted from Van Der Waals' real gas equation. The values for a and b were
obtained from Table 3.3 in the chemical engineering chapter on gas calculations
by Himmelbau cited in the reference section. When working gas law equations with
R or other constants, it is important that the values used have consistent
units. (For example, it is common for R to be listed in units of l-ata/K-mole.
This means pressure must be in ata and volume must be in liters for the obtained
solution to be correct. The units for constants a and b in the Van Der Waals'
equation must be consistent with the units chosen for R, pressure, and
temperature. Tables listing values for R, a, and b with a variety of units are
available.)
REAL (VAN DER WAALS' EQUATION) SOLUTION
Using:
Van Der Waals' Equation of State:
(P + an2/V2) (V -nb) = nRT
Rearranging:
P = nRT
- n2a
(V-nb) V2
Substituting:
P = (100 mole)(0.0821 L-ata/K moles)(298 K) - (100 mole)2 (1.33 L2-atm/mole2)
(11.3 l - 0.036 L/mole (100 mole))
(11.3
L)2
P
= 213.58 ata (This corresponds to
3139 psia or 3124 psig)
NOTE: There is a difference between the pressure obtained from the real relationship (3124 psig) and the ideal equation (3168 psig) for the pressure exerted by the same physical quantity (100 moles) in the same volume scuba cylinder. For most recreational scuba diving, this difference (about 1.4% for air) is insignificant. However, when pressures of gases are used to determine the composition of breathing gases other than air, then the difference between the real gas composition and the gas composition predicted from the simpler, ideal gas behavior can be life threatening. This difference is particularly true for helium containing mixtures.
COMPRESSIBILITY
Another approach to resolving the dilemma between ideal and real behavior
is the concept of compressibility. In this scheme, the formula for predicting
gas behavior is
PV = znRT where
z =
compressibility factor
Once
again, science introduces a constant (an empirically derived measurement) to
make an equation fit reality. The value z is different for each gas and varies
with the pressure and temperature. Tables and graphs to find the appropriate
"z-factor" at needed conditions are available. Note that for an ideal
gas, z = 1 and the real "compressibility" equation reduces to the
ideal gas law.
BEYOND REAL
The
Ideal gas equations adequately predict gas behavior at conditions near STP. As
conditions move away from STP, more terms have to be added to the equations so
that the predictions are close to observed values of pressure, temperature,
volume, and composition. These new terms gave rise to the real gas law. The real
gas equation of Van Der Waals provides enough correlation with observed values
to be used at scuba cylinder pressures. However, as the pressure continues to
increase, the so-called real gas law begins to deviate from observed values and
additional terms must be added to this real equation in order for calculated
values to correlate with observed gas behavior. These equations are well beyond
the scope of recreational diving.
CONCLUSION
Lou Fead, the "Easy Diver," said it best with "Dive with your brains, not your back!" Understanding the physical principles that govern the environment in which you have chosen to play will enhance both your enjoyment and your safety as you emerge yourself in Planet Ocean.
ADDITIONAL READING
Ames,
JS, The Free Expansion Of Gases: Memoirs of Gay-Lussac, Joule and Joule and
Thompson, Harper and Brothers Publishers, New York, 1898
Barus,
C Harper's Scientific Memoirs: The Laws of Gases, Harper & Brothers
Publishers, New York, 1899
Blake.
W & Mossman, Matheson Gas Data Book, Matheson Gas Products, Milwaukee, 1971,
p 273
Boyle, R. New Experiments Phyiomechanical Touching The Spring Of The Air And Its Effects, a chapter in Runes D (Ed) Treasury of World Science, Littlefield Adams& Co, Patterson, NJ. 1962, 73-94.
Calhoun,
F Physics For Divers, NAUI, Colton, 1978
Carlucci,
P Pletzke, T. & Peuglar, R. Gas Mixtures: Facts & Fables, Matheson Gas
Products, Secaucus,1991
Dickens,
R The Physics And Engineering Of Diving, D.L.S. Enterprises, Jacksonville,1981
Hammelblau,
DM Basic Principles and Calculations in Chemical Engineering, Prentice-Hall,
1982, p. 224
Parbrook,
G Davis, P & Parbrook, E Basic Physics And Measurement In Anesthesia,
Butterworth-Heinemann Ltd, Boston, 1990
Scornavacca,
F Gas-Mixtures: Facts & Fables, Matheson Gas Products, Secaucus, 1975
Snider,
E (Ed.) V1: Introduction & Computations For Gases, 1980:
V4:Ideal Gas Law, Enthalpy, Heat Capacity, Heats Of Solution And Mixing,
American Institute Of Chemical Engineers, New York, 1984
Tucker,
D & Gazey, B Applied Underwater Acoustics, Pergamon, New York, 1977
Weast,
RC Handbook of Chemistry and Physics, CRC Press, Boca Rotan, 1973a, pp. F-11,
B-16
Weast,
RC Handbook of Chemistry and Physics, CRC Press, Boca Rotan, 1973b, D-157
Webb,
.P Thermal Problems, A chapter in Bennett, P & Elliot, D The Physiology and
Medicine of Diving, Best Publishing, San Pedro, 1982, p. 302
Wienke,
B Basic Diving Physics And Applications, Best Publishing, Flagstaff, 1994
Wienke, B Basic Technical Diving In Depth, Best Publishing, Flagstaff, 2001
Jump To: Kinetic Absolute Values Charles Guy-Lussac Boyle General Dalton Henry Real VanDer Waal
Go To: Home About "Harris" Articles Slides War Stories Editorials Links Fini
Credit:
Portions of this article were used in my chapter on Dive Physics appearing in:
Bove and Davis' Diving Medicine (4 th Edition), published by Saunders (Elsevier)
About
The Author:
Larry "Harris" Taylor, Ph.D. is a biochemist and Diving Safety Coordinator at the University of Michigan. He has authored more than 200 scuba related articles. His personal dive library (See Alert Diver, Mar/Apr, 1997, p. 54) is considered one of the best recreational sources of information In North America.
All rights reserved.
Use of these articles for personal or organizational profit is specifically denied.
These articles may be used for not-for-profit diving education