
Archimedes, A Gold Thief and Buoyancy
by
Larry "Harris" Taylor, Ph.D.
This
is an electronic reprint and expansion of an article that appeared in SOURCES
(July/Aug. 1993, p. 27-30). This material is copyrighted and all rights retained
by the author. This article is made available as a service to the diving
community by the author and may be distributed for any non-commercial or
Not-For-Profit use.
All rights reserved.
Go To: Home About "Harris" Articles Slides War Stories Editorials Links Fini
Once upon a time (the 3 rd century B.C.) there was a very wealthy king. Like most kings, Hiero of Syracuse (on the island of modern day Sicily) wore a crown as a symbol of his authority. Over the years, Hiero was made aware that his Royal Goldsmith (who made his crown from Hiero's treasury) was living a lifestyle that was beyond his means. Hiero suspected that the Royal Goldsmith was using royal gold, intended for the royal crown, to augment his personal wealth. The goldsmith was rumored to be preparing the crowns with a cheaper alloy (using a silver-gold mix) than pure gold. No one using 3 rd century B.C. technology knew how to prove or disprove the speculation that the Royal Goldsmith was "stealing from the crown."
The problem of determining the
gold content of the royal crown was given to Archimedes, a noted Greek
mathematician and natural philosopher. Needles to say, this was not a trivial
problem! Archimedes knew that silver was less dense than gold, but did not know
any way of determining the relative the density (mass/volume) of an irregularly
shaped crown, The weight could be determined using a balance or scale, but the
only way known to determine volume, using the geometry of the day, was to beat
the crown into a solid sphere or cube. Since Hiero had specified that damage to
the crown would be viewed with less than enthusiasm, Archimedes did not wish to
risk the king's wrath by pounding the crown into a cube and hoping that
post-analysis it could be made all better again.
While in the public baths,
Archimedes observed that the level of water rose in the tub when he entered the
bath. He realized this was the solution to his problem and supposedly, in his
excitement, he leaped up and ran naked through the streets back to his
laboratory screaming "Eureka, Eureka!" (I've got it!).
Later, he demonstrated to Hiero
and his court how the amount of water overflowing a tub could be used to measure
a volume. His calculations indicated the goldsmith was, indeed, an embezzler.
History does not record the fate of the unscrupulous artisan.
Archimedes observation has been
formalized into Archimedes Principle:
"An object partially or wholly immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object."
Translation: objects more dense
than water (like lead) will sink; objects less dense than water (like cork) will
float; objects of the same density will remain at the same level (hover) and
neither sink nor float. Objects that sink are frequently termed negatively
buoyant. Objects that float are termed positively buoyant. Objects that stay
stationary at depth are said to be neutrally buoyant.
Buoyancy is easiest understood
by the application of "force arrow" principles or vectors. Vectors are
mathematical constructs that have magnitude (like mass) and direction (towards
or away from the surface). Weight is a downward force (gravity acting on mass);
buoyancy is an upward force. If these two forces are balanced, then so-called
neutral buoyancy (object hovers) is achieved. If they are not balanced, the
object immersed will either sink (weight greater than upward buoyant force) or
float (weight less than upward buoyant force).
NOTE: As with weight and
mass, divers commonly are imprecise in the use of the term buoyancy. Rigorously,
buoyancy is defined as ONLY an upward force directed against the force of
weight. Although commonly used in the diving community, the terms
"neutrally buoyant" and "negatively buoyant" are rigorously
improper; the term "positively buoyant" is redundant. Buoyancy is much
easier to understand if one only considers balancing an upward force (buoyancy)
and a downward force (weight). In this scheme, there is no positive or negative.
We will use the term "hover" to refer to the so-called "neutrally
buoyant" state. Thus, an object will float, hover or sink. If weight is
greater than buoyancy, the object sinks. If buoyancy is greater than weight, the
object rises. If weight and buoyancy are identical, then the object hovers
("is weightless")
EXAMPLE: When a helicopter
"hovers." (Remains stationary and neither rises or sinks) the
helicopter has exactly balanced the downward force of weight with the upward
force of lift supplied by the turning rotor. A diver "hovers" by
balancing the downward force of weight with the upward force of buoyancy.
For the diver, the force of buoyancy (yellow arrow, below) ALWAYS acts to move the diver (immersed object) towards the surface. Weight (red arrow, below) ALWAYS acts to move the diver (immersed object) towards the bottom. These forces are either balanced (identical) or unbalanced. If they are NOT balanced (the ideal "hovering" or weightless condition), then the diver MUST expend energy to maintain a horizontal steady state.

Buoyancy Largest = Ascend
Forces Balanced = Hover
Weight Largest = Sink
Most buoyancy issues (either solving buoyancy physics problems or in-water diving) can be understood by simply determining the relationship between forces acting either up or down.
Buoyancy-type problems involve
three factors: the weight of the object being submerged, the volume of the
object submerged, and the density of the liquid involved in the problem. Any two
of these factors can be used to determine the third. Let's study some
representative numeric examples.
ENGLISH EXAMPLE:
What is the buoyancy in seawater of a piece of wood that weighs 2000 pounds
& measures 6 ft x 2 ft x 3 ft?
ANSWER: Determine
forces involved:
a. The weight of wood
= 2000 pounds
b. The volume of wood
= 6 ft x 2 ft x 3 ft = 36 ft3
c. The corresponding
weight of an equal volume of seawater
36 ft3
x 64 lb / ft3
= 2304 lb
At this point, we know that the
wood object weighs less than the corresponding volume of water (the volume of
seawater that would be displaced if the entire object were to be submerged),
thus it will float.
Applying "force
arrows:"
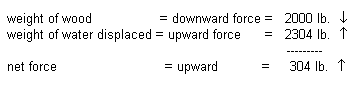
The object will float with a
buoyant force of 304 pounds. In order to sink the object, the object would have
to weigh more than an additional 304 pounds (without changing volume.) This is
the amount of "push" you would have to exert on this log for it to
sink. Although the object is buoyant (i.e., there is a net force of 304 pounds
pushing up on this log), it will not be completely out of the water. The density
of the log can then be used to determine how much of the log will be
submerged.
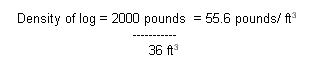
Since this log is less dense
than seawater, it will float. The amount of the volume that is submerged will be
determined by the ratio of the density of the log and the density of the
seawater. In general:
Ratio: Volume Submerged =
Density Object / Density Liquid
Substituting the value of this
log & seawater:
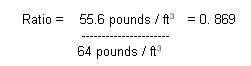
So,
about 87% of the log's volume will be submerged.
ENGLISH EXAMPLE:
A fully suited diver weighs 200 pounds. This diver
displaces a volume of 3.0 cubic feet of seawater. Will the diver float or sink?
ANSWER:
Determine forces involved:
a. weight of equal volume of
seawater:
3.0
ft3 x 64
lb / ft3. =
192 lb.
b. applying force arrows:
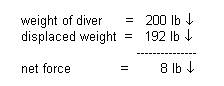
The diver will sink. This diver
weighs 8 pounds in the water and is severely over-weighted. Removal of eight
pounds will allow the diver to hover (which means the diver will have to do less
work while diving; see the trim discussion.) Since the object of recreational
diving is to enjoy the environment, less work translates into more bottom time
and more fun!
ENGLISH EXAMPLE:
A fully geared diver in a wet suit weighs 210 pounds. In fresh water, this diver
with a scuba cylinder containing 500 psig needs 18 pounds of lead to hover. How
much lead will this diver need when diving in a wet suit in seawater?
ANSWER: Using
Force Arrows:

To hover, the volume of water
displaced by the diver must exert a buoyant force upward equal the total weight
of the diver plus gear (downward force). This is the buoyant force exerted by a
volume of fresh water (density = 62.4 lb./cubic foot) that weighs 228
pounds.
Determine Volume of
diver:
Density = Mass / Volume
Rearranging:
Volume =
Mass / Density
Substituting:
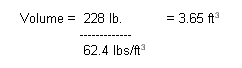
Now that we know the volume of
the diver, we can determine (with the assumption the volume of the weight belt
is negligible) the buoyant force from the seawater (density 64 lb./ cubic foot)
the diver would displace:
3.65 ft3 x
64 lb / ft3
= 233.6 lb.
Applying force arrows:

So, the diver that was
comfortable with eighteen pounds of lead on the weight belt in fresh water must
add 6 more pounds (for a total of 24 lb.) on the weight belt to dive in
seawater.
ENGLISH EXAMPLE:
A fully geared diver in a wet suit weighs 210 pounds. In seawater, this diver
needs 18 pounds of lead to hover. How much lead will this diver need when diving
in a wet suit in fresh water?
ANSWER: Using
Force Arrows:

To hover, the volume of water
displaced by the diver must exert an upward buoyant force equal the total weight
of the diver plus gear (downward force). This is the upward buoyant force
exerted by the displaced volume of seawater (density = 64 lb./cubic foot) that
weighs 228 pounds.
Determine Volume of diver:
(Divers use weight and mass as equivalent terms)
Density = Weight / Volume
Rearranging:
Volume =
Weight / Density
Substituting:
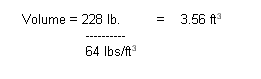
Now that we know the volume of
the diver, we can determine the upward buoyant force from fresh water (density
62.4 lb./ cubic foot) the diver would displace:
3.56 ft3 x
62.4 lb / ft3
= 222.1 lb.
Applying force arrows:

So, the diver that was
comfortable with eighteen pounds of lead on the weight belt in seawater must
remove 6 pounds (for a total of 12 lb.) from the weight belt to dive in fresh
water. The difference in density between fresh and seawater is the reason why
different amounts of weight must be used when diving in different environments.
When moving from fresh to seawater (with the same equipment configuration),
divers must add weight. When moving from seawater to less dense fresh water,
divers should remove weight.
METRIC EXAMPLE:
A log weighing 6000 kg measures 1 m x 3 m x 2 m. Will this object sink or float
in seawater (density = 1.0256 kg/l)?
ANSWER: Determine
volume of object:
Volume = 1 m x 3 m x
2 m = 6 m3
Convert cubic meters to
liters:
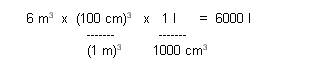
Determine weight of the
displaced water:
6,000 l x
1.0256 kg/ l =
6,154 kg
Using force arrows:

Now we know that this object
will float
METRIC EXAMPLE:
How much of the log will be submerged?
ANSWER:
Determine density of object:
Density = Weight / Volume

The amount that will be
submerged is the ratio of densities:
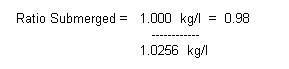
So, about 98% of this object will be submerged in seawater.
METRIC EXAMPLE: A wet suited diver weighs 74 kg with gear. The diver has a volume of 80 l. How much lead should the diver wear for diving in seawater (density = 1.026 kg/l)?
ANSWER:
Determine weight of seawater displaced:
80 l x 1.026 kg / l
= 82.1 kg
Using force arrows:

Since there is a resultant
buoyant force of 8 kg, the diver will have to wear 8 kg to compensate.
Divers wearing wet or dry suits
have an additional factor to consider. Within the wet suit are trapped bubbles
of gas; a dry suit diver has air spaces between the diver and the suit. This gas
(in fact, all air spaces) is subject to changes in volume as a result of changes
in pressure (See Boyle's Law). This means that as the diver moves up or down in
the water column, the volume of these gas spaces changes. This change in gas
volume affects the diver's buoyancy. As a diver descends, the volume of the gas
decreases. Thus, less water is displaced. The diver is less buoyant and sinks.
On ascent, the pressure on the diver decreases. The gas expands and occupies a
larger volume. This displaces more water and increases the buoyant (upward)
force.
Archimedes principle points out
that if we are not hovering, we MUST be either floating (moving up) or sinking.
So, unless our buoyancy and weight are equal, we must expend energy to hover in
the water column. However, if the buoyant force exactly matches the downward
force contributed by the weight of the object submerged, then a
"weightless" state is achieved. This is why NASA uses underwater
training for its astronauts. By finely tuning the buoyancy of a space-suited
astronaut underwater, the weightless environment of space can be simulated. This
allows astronauts the opportunity to practice (using the philosophy that
"Perfect Practice and Prior Planning Precedes Perfect Performance!) their
mission on earth to ensure success in space.
The lift associated with air
spaces can be used to raise objects from the bottom. Since air weighs very
little compared to the weight of the displaced water, it can be assumed that the
lifting capacity is equal to the weight of the volume of water that is displaced
by the air volume of the lifting device.
ENGLISH EXAMPLE:
You wish to lift a 300-pound anchor from the bottom of a lake bed. The bottom is
hard and flat (so no excess lift will be needed to overcome the suction
associated with being immersed in the bottom muck). You have access to 55 gal
drums (weighing 20 pounds each) that have been fitted with over-expansion vents.
How many 55 gal drums will it take to lift the anchor?
ANSWER: Determine
forces involved:
a. Determine weight of
water displaced:
Weight = Density x
Volume
Lake implies fresh water: density = 62.4 lbs/ft3
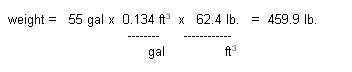
Applying force arrows:
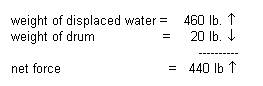
Since the object to be lifted
weighs less than the 440-pound lifting capacity of a 55 gal drum, a single 55
gallon drum should be sufficient to lift the 300 pound anchor. In practice,
large lifting objects (like a 55 gal drum) have a large surface area and will
generate considerable drag (which decreases lifting capacity). Without getting
mathematically rigorous and calculating drag coefficients, a safe rule of thumb
is to assume about 0.75 of the calculated lifting capacity for the lifting
device in an actual lifting operation.
PROBLEM:
Which weighs more underwater: a pound of lead or a pound of concrete?
ANSWER:
Although both weigh the same on the surface, lead will weigh more while
totally submerged. Rationale: Lead is more dense than concrete, thus an equal
weight will displace less volume of water. Lead will therefore have less
buoyancy counteracting its weight and thus its underwater weight will be
greater.
TRIM
As a diver moves in the water
column, the diver is subject to a number of forces. In the vertical plane,
gravity (weight) tends to make the diver descend and buoyancy (from too little
weight or too much air in the b.c.d.) makes the diver ascend. In the horizontal
plane, the diver moves forward propelled by the force of the kick. The thrust,
or forward motion, must overcome drag (or friction) that the diver and equipment
present to the water. A good diver tries to adjust diving style to balance the
forces involved.
Part of the unique exhilaration
of diving is the ability to glide, weightless, under the surface of the water.
It is the most efficient and enjoyable way to dive. If the diver is over
weighted (a too common occurrence), then s/he must continually expend energy to
overcome gravity and remain at constant depth. If the diver is under weighted,
s/he must also continually expend energy in an attempt to overcome buoyancy with
leg power. (In battles with the forces of buoyancy and weight, these forces
always overcome leg power and fatigue is certain.) The way to maximize
efficiency (decrease work load and thus increase enjoyment) in the water is to
balance weight and buoyancy so that the thrust from the fins can be directed
towards forward movement, not towards overcoming buoyancy errors.
Assuming a horizontal position in the water can reduce drag. The more horizontal the diver, the less drag (resistance to movement caused by friction between the diver and the dense water environment) will occur and the easier underwater swimming will be! In general, cutting the cross-sectional area by a factor of two requires four times less energy to go the same distance. A more horizontal position presents a smaller area to the path of movement and thus lessens resistance.
Bottom
line:
Understanding the interaction of the forces of weight and buoyancy will help a diver achieve weightless diving. The concepts associated with buoyancy control are a superb example of the Easy Diver's principle of "Dive with your brains, not your back!"
Go To: Home About "Harris" Articles Slides War Stories Editorials Links Fini
Credit:
Portions of this article were used in my chapter on Dive Physics appearing in:
Bove and Davis' Diving Medicine (4 th Edition), published by Saunders (Elsevier)
This
article has been translated into Russian: ru-archimedes
About
the author:
Larry
"Harris" Taylor, Ph.D. is a biochemist and Diving Safety Coordinator
at the University of Michigan. He has authored more than 200 scuba related
articles. His personal dive library (See Alert Diver, Mar/Apr, 1997, p. 54) is
considered one of the best recreational sources of information In North America.
All rights reserved.
Use of these articles for personal or organizational profit is specifically denied.
These articles may be used for not-for-profit diving education