Current Navigation

River Diving: The Vector Approach To Navigation

Larry "Harris" Taylor, Ph.D.

This is an electronic reprint and expansion of the article that appeared in NAUI News (Mar/Apr. 1988, 18-21). This material is copyrighted. All rights are retained by the author. This article is made available as a service to the diving community by the author and may be distributed for any non-commercial or Not-For-Profit use. All rights reserved

Go To: Home About "Harris" Articles Slides War Stories Editorials Links Fini

Many diving students are intimidated by the art of navigation. After all, most navigational texts are filled with seemingly complex and rigorous mathematical equations. When one adds to this the wizardry and rituals often associated with at-sea navigation, it is easy to understand why students are so intimidated by the subject of navigation, that they fail to see how simple much of practical navigation can truly be.

Historically, there was a reason to make navigation appear complex and beyond the realm of all but the most gifted of sailors. The reason for the deception of those practicing the navigational arts was simple: survival. The conditions of early sailing vessels were often less than humane and the ritual of navigation prevented many a mutiny. As a matter of fact, many ship's masters often went to great lengths to ritualize the art of navigation in an effort to convince ordinary seaman that they could never master the art. No matter how distastefully the sailors felt they had been treated, rebellion against the captain and mate was a mutiny against those who were the only ones capable of finding the way home. Thus seaman endured, rather than dispose of the way home. For the most part, scuba instructors are not worried about such open rebellion and there should be no need to perpetuate the myth that navigation is exceedingly complex and difficult.

First of all, navigation by any technique, is not foolproof! Navigation (the art of safely going from one place to a second desired location) really boils down to the art of estimating and correcting errors. Navigational techniques apply certain assumptions such as:

1. the diver swims at a constant rate of speed in a straight line and

2. currents are constant in both speed and direction.

However, since Mother Nature, the Diver and "Murphy's Law" do not really operate in such a manner, all navigation techniques should be viewed as a "best guess" estimate. The trick is to make that guess come close to reality. Experience with self in the water environment, Mother Nature and Murphy will allow one to know the conditions under which the various navigational techniques will be useful.

In order to estimate a diver's position in a current with time, one must first know the speed at which the diver swims. Typically, this is determined by having the diver swim 100 ft along a measured line with no current influences. (My students swim 3 separate 100 ft. lengths and determine the average number of kicks, the time taken, and the air consumed.) Next, one must know the speed and direction of the current. In coastal situations this can be estimated by consulting tide tables. There are procedures and separate tables for estimating both horizontal and vertical water movement in a tidal zone. In the absence of instrumentation, a commonly employed in a river situation method involves trailing a float on a 100 ft. line behind an anchor point or, more simply, marking a 100 foot segment on land and having an observer note the taken to float the length of the measured line. The current speed can then be calculated or estimates can be made from a current speed table as shown below.

Speed As a Function of Time Taken To Travel 100 Feet

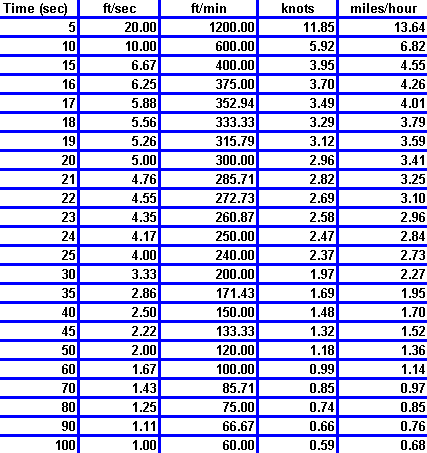
A bearing from the anchor point to the float gives the direction to which the current is moving. The current direction is this value. (Wind directions are reported from where they originate, current directions are reported in the direction to which they are moving.) We will examine two different approaches to dealing with currents. The first (and by far, the most common ) is to assume that there is no effect and that the diver need not concern himself with them. 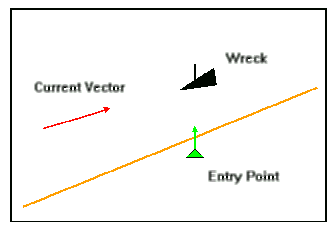Let us assume a macho diver wishes to explore an old river steamer that lies due north (course 000) of his convenient entry point 500 ft offshore. There is a current of 50 ft/min (about 1/2 knot) moving towards true bearing 075 (the current direction is thus 075; current directions are given as the direction to which they move). The situation is shown below:

The diver just finished a scuba class and thus we know that he swims a 100 ft. distance in 1.5 minutes. This diver is a very powerful person on land and thus he assumes that his physical prowess will allow him to swim directly to the wreck. So, he enters the water. Let's see what effect the current will have on this macho diver. We estimate his speed:

1.5 min / 100 ft => 100 ft / 1.5 min = 66.7 ft/ min

We estimate his travel time to the wreck:

500 ft / 66.7 ft/min = 7.5 min

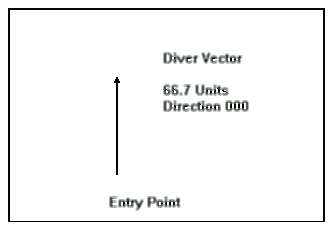
We now resort to vectors. A vector is merely a line that is drawn to scale that conveys information of both magnitude (how much?) and direction (to where?). Although it is possible to do our estimations using simple or not-so-simple trigonometric equations, drawing lines with a ruler and protractor on graph paper (or better yet, the actual nautical chart) is simpler and for the most part faster. We begin by drawing a line which represents the diver moving through the water. This line is drawn in the direction the diver swims (due north, course 000) and is 66.7 units long. The actual size of a unit is unimportant; what is important is that all additional lines are of the same scale and units. (For example one does not plot mph with ft / min.) Our line is 66.7 units long because our macho diver is swimming at a rate of 66.7 ft / min. We place an "arrow head" on the "northern" end because this is the direction our diver is moving.

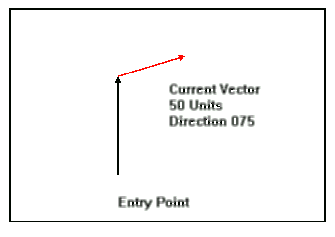
Next, we draw a line representing the effect of the current on our diver. This line is 50 units long (for 50 ft / min ) and is drawn heading in the direction 075. Note that we place the "tail" of the current vector on the "head" of the diver speed vector. (We are actually performing vector addition.)

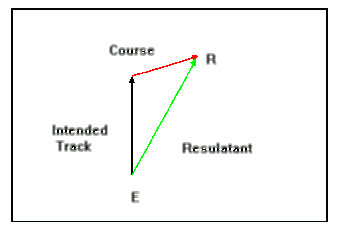
Then, we draw a "resultant" (connect point E, the entry point, to R, the result). This line represents the effect of the current on the path the diver will swim. In other words, a diver swimming at a heading of 000 at a constant speed of 66.7 feet per minute under the influence pf a 50 feet per minute current directed towards true course 075 will swim along a path approximated by the resultant line.

Since we very cleverly chose our units so that each separate vector was one minute in time, we can estimate the macho diver's position after swimming 7.5 minutes by using dividers (or a ruler). We measure the distance E to R and then measure 7.5 times this distance from E along an extended resultant line. This position (D, for disaster) represents where macho man will be when he thinks he should be at the wreck. Measuring (to scale) the distance from the wreck to D indicates the macho man to be about 380 ft. from the wreck.

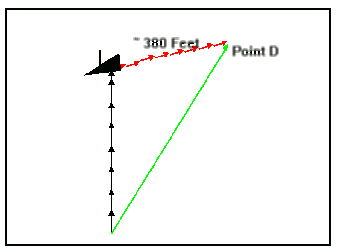
This explains why macho diver surfaced so far from the wreck.

Fortunately, his great physical prowess made the walk back to the entry point with his gear no big deal.

Another diver, Wimpy, decides to make this dive. He knows it is possible to partially counteract the force of the current by swimming at an angle into the current. He uses a ruler, protractor, and a drawing compass to determine his course. First, he draws a long line in the direction he wants to swim. In this case, course 000 or due north. This line is called the intended track. He labels the entry point E.

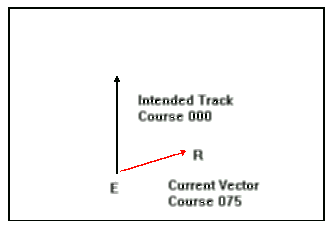
Next, he draws a current vector 50 units long (for 50 ft/ min) FROM THE ENTRY POINT, E, towards true direction 075. This point, R, represents the effect of the current on the diver with the diver doing no swimming.

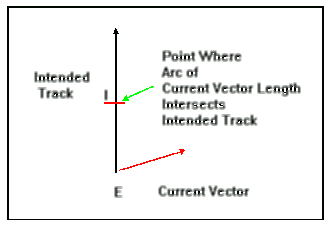
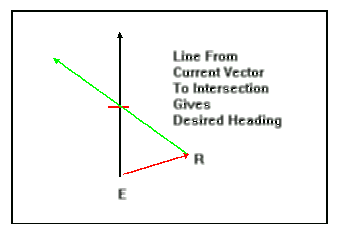
Using a drawing compass, Wimpy draws an arc of radius 66.7 units representing his speed of 66.7 ft / min. (Fortunately for this example, Wimpy and macho man swim at the same speed; Wimpy just uses 1/3 the air!) using point R as the center point. This arc intersects the intended track at point I.

Now, he draws a line from point R to the intersection point, I. This line represents the course needed to follow at a constant speed of 66.7 ft/min in order to counteract the effect of the current and to swim along the intended track. In this case, the line corresponds to a true course of 315. Although he will be swimming facing heading 315, his actual path will be along the intended track. The last navigating step before the dive is to determine the compass course to be used. Since Wimpy lives in an area where the variation is 003 E, he sets his compass bezel for a course of 312.

Summary: In order to swim to a wreck that lies 500 ft due north in a constant current of 50 ft/ min moving toward a true direction of 075, it is necessary for a diver to swim at a compass course of 312 at a constant speed of 66.7 ft / min. Wimpy and his buddy made the dive and discovered that the rumors of gambler's gold aboard the wreck were based on fact. Wimpy now is driven to the dive site and does his plotting with platinum dividers.

Several weeks later after spring rains, both divers returned to the same spot. However, the current is now 300 ft / min (about 3 knots). Macho man entered the water, figuring that by swimming straight into the current, he would manage to find the wreck. Wimpy, using his platinum dividers analyzed the situation using vectors.

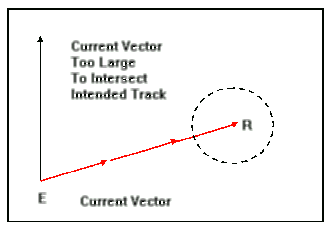
In this case, the diver speed radius does not intersect the intended track. This means that it is not possible for the diver to make the intended dive under the conditions specified. Thus, there is no way (without mechanical assistance) for this dive to be made from this entry point. Wimpy decides he wants to dive and uses vectors to help determine a new entry point. Starting from the wreck, he draws the reciprocal of the current vector (300 units in direction 255). To this, he adds the reciprocal of his speed vector (66.7 units in direction 180). He then extends the resultant line to shore on the chart.

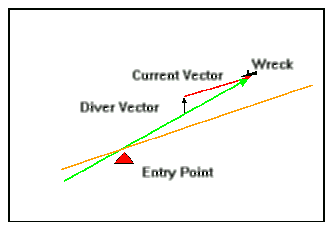
Here, the line crosses shore about 1080 feet upstream from the point where macho man was last seen. This is his new entry point. Although Wimpy has calculated that the dive was possible (on paper), he decides he has not yet had enough experience to make a dive in this current.

If there would have been no intersection of the resultant line with shore, then other options must be considered:

a. swim faster to increase the diver's speed vector

b. use a DPV

c. convince someone to lay cable guidelines to the wreck

d. buy a boat

e. dive from someone else's boat

f. abort the dive.

Conclusion

The vector method of estimating a diver's position in current is not perfect. It assumes that factors stay constant when we live in a universe of constant variability. However, it does provide a basis for reasonable estimation. In fact, as long as the distance involved is short, this method provides excellent correlation with reality. Lou Fead (The "Easy Diver") said it best, "Dive with your brains, not your back!" If you dive in current, using graph paper, a compass, a protractor, and a few drawn lines can save you hours of frustration in the water, as well as eliminating some very long walks back to entry points.

This is one portion of series of articles on river diving. Others are

River Diving: Reading Rivers River Diving: Equipment River Diving: Technique

Lecture Slides for the river diving course at River

Top

Go To: Home About "Harris" Articles Slides War Stories Editorials Links Fini

About The Author:

Larry "Harris" Taylor, Ph.D. is a biochemist and Diving Safety Coordinator at the University of Michigan. He has authored more than 100 scuba related articles. His personal dive library (See Alert Diver, Mar/Apr, 1997, p. 54) is considered one of the best recreational sources of information In North America.

Use of these articles for personal or organizational profit is specifically denied.

These articles may be used for not-for-profit diving education