Chapter 0 of "Classical and Connectionist Models of Cognition"
MIT Ph.D. Dissertation, 1991
Much of the philosophical interest of cognitive science stems from its potential relevance to the mind/body problem. The mind/body problem concerns whether both mental and physical phenomena exist, and if so, whether they are distinct. In this chapter I want to portray the classical and connectionist frameworks in cognitive science as potential sources of evidence for or against a particular strategy for solving the mind/body problem. It is not my aim to offer a full assessment of these two frameworks in this capacity. Instead, in this thesis I will deal with three philosophical issues which are (at best) preliminaries to such an assessment: issues about the syntax, the semantics, and the processing of the mental representations countenanced by classical and connectionist models. I will characterize these three issues in more detail at the end of the chapter.
0.1.1 Functionalism and Token Physicalism
From a highly abstract but useful perspective, cognitive science is a kind of test for a particular philosophical theory of mental phenomena, namely, functionalism (see the related articles in Block, 1980). While functionalism can be cast as a general claim about all mental phenomena, it is most usefully introduced as an account of particular types of mental states or events. What is it to be a functionalist about a type of mental occurrence<1> M, such as thinking that sugar is white, wishing that one's teeth were as white as sugar, planning to eat more sugar, having a toothache, or being in a bad mood? A functionalist identifies M with a particular functional state or event type. Functional types are those which are individuated solely by considerations of causal relations. A state or event token f belongs to a functional type F if and only if f participates in causal relations of the sort which define F; in this case we may say that f has an "F-role". This means that a functionalist about a mental state or event M must specify the causal relations-- the M-role--taken to be necessary and sufficient for a state or event token m to be of type M. This is standardly done by specifying causal generalizations or laws which relate tokens of type M (under certain conditions) to external occurrences (e.g., through sensory or motor processes), and to other internal occurrences (e.g., through inferential or computational processes). Functionalists typically hope that as cognitive science develops, they will be better able to specify these generalizations and laws, and so will be able to specify in greater detail which functional types are identical with which mental types.
How can this be worked into a solution to the mind/body problem (at least for those mental occurrences to which functionalism is applied)? The standard hypothesis is that there are physical state or event tokens which satisfy the functionalist's causal generalizations and laws, and are therefore tokens of mental types.<2> Given this hypothesis, then, it is possible to adopt the position known as "token physicalism" (about M): each token mental state or event m of type M is identical to a token physical state or event b.<3> The token physicalist answer to the mind/body problem, then, is that both mental and physical phenomena exist, but that (at least in certain cases) they are not distinct.
The functionalist and token physicalist approach to the mind/body problem can only work if token physical states or events can enter into the causal relations specified by functionalism. This raises what might be called (not the mind/body problem but) the "mental-body problem": how is it possible for a physical system to implement the requisite processes of sensation, motor control, inference, memory, and so on?<4> To answer this question, we need to formulate specific claims about the nature of the token physical occurrences located by functionalism (e.g., b in the previous paragraph).
A useful way to highlight issues about mental representations is to focus only on functionalist theories of "propositional attitudes"--certain mental states, such as thoughts, wishes, and plans, which have propositional content.<5> It seems likely from a functionalist standpoint that some inferential relations are components of propositional-attitude-roles (although it is notoriously difficult to specify these relations). To explain how physical states can implement these inferential processes, cognitive scientists have traditionally appealed to an analogy with the ways computers implement algorithms. Several philosophers have tried to extract from this analogy specific, substantive claims about the physical embodiments of propositional attitude types. The two most important claims for my purposes are representationalism and the language-of-thought (LOT) hypothesis, as formulated in a number of works by Jerry Fodor. These claims characterize what is common to classical models in cognitive science.
It is an intuitively obvious but theoretically striking fact that a person can have many different attitudes with the same propositional content. We can perceive that toothpaste is white, believe (to various degrees) that it is, and hypothesize, imagine, or desire (to various degrees) that it is. Indeed, it seems that we never find people who are able to have one of these attitudes toward a given proposition, but are unable to have another one of these attitudes toward the same content. Furthermore, there seem to be widespread, regular, and important causal relations between different attitudes to the same proposition: for example, perceiving that p tends to cause believing that p, while doubting that p tends to interact with wishing that p to generate action. Whatever the ultimate details, these causal and presuppositional relations are likely factors in any functionalist account of propositional attitudes. We can therefore formulate a special case of the mental-body problem: how is it possible for these special relations to be implemented in a physical system?<6> This question is raised, but not answered, by functionalism and token physicalism about propositional attitudes. Representationalism seeks to supply an answer to this question (among others--see Fodor, 1981).
Understandably, representationalism is sometimes simply put as the claim that there are mental representations--entities with content mediating between sensation and motor control-- and that these representations are (by token physicalism) physical. However, this formulation does not reveal any claim stronger than token physicalism about propositional attitudes. Any such token physicalism postulates physical states which, as token mental states, mediate between sensation and motor control, and which, as token attitudes with propositional content, are representations. If representationalism is to yield an explanation of how physical systems can implement special relations among attitudes toward the same content, we need a construal which specifies in more detail the nature of token propositional attitudes.
The standard strategy is to treat propositional attitudes as computational relations between thinkers and physical representations. It will help to formulate this idea if we consider an arbitrarily chosen propositional-attitude type, say, the attitude A with the content that p. Also, let t be a variable ranging over the thinkers (i.e., potential A-ers that p) to which representationalism is applied (i.e., representationalism about A-ing that p). The claim (to be modified shortly) is as follows:
(At least typically) t's A-ing that p is identical with t's having a certain computational relation to a physical representation r with the content that p.
Since (as explained in the previous paragraph) token physicalism, even without representationalism, "already" postulates physical representations that p, any extra force of this claim must stem from its appeal to "a certain computational relation".
Unfortunately, the notion of a computational relation is typically left unclear, and the specification of which relations are appropriate for which attitudes is typically left to the development of cognitive science. This leads back to the worry that the standard formulation of representationalism fails to add any substance to functionalism and token physicalism (about A-ing that p). By functionalism, any token occurrence of A-ing that p has a particular inferential role. It follows from this that any such occurrence stands in some computational relation to its thinker t.<7> Without specific constraints, then, t's A-ing that p satisfies the requirements for r. As a result, the current formulation of representationalism fails to require the postulation of any representations other than those "already" postulated by functionalism and token physicalism.
To strengthen representationalism, we might simply add to the formulation the clause that r is distinct from t's A-ing that p. However, this is compatible with r's being identical to some other propositional attitude, and so this revision would not insure that representationalism is stronger than functionalism and token physicalism about propositional attitudes in general. For this reason, I am inclined to take representationalism as claiming that r is not a propositional attitude at all. This may be puzzling at first, since r is supposed to be a mental representation that p. How can something be a mental representation that p without being a propositional attitude that p? So far as I know, there is only one way for this to happen: r must be a propositional idea--an idea with the content that p.<8> So representationalism comes to the claim that propositional attitudes that p are typically computational relations to propositional ideas that p. It is incumbent upon the representationalist, then, to give an account of the difference between propositional ideas and propositional attitudes.
Having an idea that p is akin (i.e., presumably identical) to what philosophers sometimes call "grasping" the proposition that p. Since representationalism is a species of functionalism about attitudes, it seems natural for the representationalist also to adopt a functionalist stance about ideas. Given this, the task is to display the respects in which the roles of ideas and attitudes differ. We can begin with a few natural claims which, though strictly speaking circular in this context, may bring out what is meant by "idea". A token idea that p (i.e., a particular thinker's idea that p) typically persists through changes in token attitudes that p. One's idea that p (i.e., one's grasp of the proposition that p) doesn't vanish when one's belief or desire that p vanishes, and indeed one can have an idea that p (and not merely in a dispositional sense) without having any attitudes that p. Second, a token idea that p is typically involved in many different token attitudes that p.<9>
What can be said by way of giving a more principled distinction between propositional attitudes and propositional ideas? My suggestion is that propositional attitudes are those mental representations which standardly function as units of reasoning. Such representations have rationality values, i.e., degrees of rationality or irrationality, which can influence the rationality values of other representations or actions, or at least be influenced by other representations or perceptions. A belief that Paris is pretty--or a wish that it were--has a rationality value. By contrast, a mere idea of Paris' being pretty is neither rational nor irrational. Beyond drawing this connection between propositional attitudes and rationality values, I have very little to say about the proper conception of rationality values. I imagine that, at a minimum, having rationality values is corequisite with having a role as a (potential) premise or conclusion of inference.<10>
However the distinction between ideas and attitudes is ultimately to be spelled out, another way to see the theoretical bite of representationalism is to display its promise as an explanation of how physical systems can implement special causal relations among different attitudes that p. The details of such an explanation vary according to the nature of the physical realization of ideas. A possibility at one extreme is that one's idea that p is realized as a token physical structure which is part of the physical structures realizing all of one's (specially related) token attitudes that p. In such a case, I will say that all of these token attitudes are relations to the same token "symbol". The special relations between these attitudes might then be explained by the fact that they literally share an ingredient, a token symbol that p. For example, if we postulate that a thinker has the capacity to have beliefs and desires at all, this explains why his ability to have beliefs that p presupposes his ability to have desires that p. A possibility at the opposite extreme is that one's idea that p is realized as a mechanism which can reproduce physical structures each of which is part of only one token attitude that p. In this case, I will say that each token attitude is a relation to a distinct token symbol of a single physical kind (defined by reference to the reproduction mechanism). Although the token symbols are distinct, if we postulate processes which can match symbols of the given physical kind, then we can also begin to understand how to implement the special relations among attitudes with the same content.<11>
0.1.3 The Language-of-Thought Hypothesis
Just as there appear to be special causal relations among different attitudes with the same content, so there appear to be special causal relations among attitudes of the same kind with different contents. For a wide variety of things we can think about (e.g., sugar, toothpaste, and teeth) thoughts that such a thing is white typically bear special causal relations not only to desires that it be white, but also to thoughts that it is not yellow, that it is white or blue, that something is white, and so on. Again, whatever the ultimate details, such causal relations are widespread, regular, and important enough to be likely factors in any functionalist account of propositional attitudes. Fodor and Pylyshyn have provided a useful characterization of similar relations in terms of what they call "systematicity" (Fodor and Pylyshyn, 1988). I will focus on the details of their treatment in chapter 1. For now, as before, we can appeal to the special causal relations to formulate another aspect of the mental-body problem: how is it possible for these systematic relations to be implemented in a physical system? The language-of-thought (LOT) hypothesis, unlike token physicalism or representationalism, is intended to serve as an answer to this question (among other questions--see Fodor, 1975; Fodor, 1987a).
The LOT hypothesis goes one step beyond representationalism, just as representationalism goes one step beyond token physicalism. According to the LOT hypothesis, the physical symbols postulated by representationalism admit of syntactic complexity. What is it for a symbol to be complex?<12> Although this is a very difficult question, we can operate with an intuitive idea, leaving technicalities aside. The prototypical complex symbols are written sentences and phrases in natural language. Each complex sentence and phrase has two or more symbols--e.g., words--as spatiotemporally proper parts, where parthood is taken quite literally (that is, as the phenomenon studied in mereology). Accordingly, syntactically complex mental symbols are thought to have other mental symbols as literal parts.<13> The parthood may be spatial, as with written sentences, or temporal, as with spoken sentences, or a mixture of the two.<14>
In addition to the requirement of symbolic parts, a semantic requirement is standardly placed on syntactic complexity. Not only do sentences and phrases have other phrases and words as parts, but they also bear some sort of close semantic relation to these parts. Fodor and Pylyshyn express this relation by saying that "the semantic content of a [complex] representation is a function of the semantic contents of its syntactic parts, together with its constituent structure" (Fodor and Pylyshyn, 1988, p. 12). In other words, without delving into too many technicalities, the content of the complex symbol must depend on the contents of its parts, as the content of "Mary loves John" depends on the content of "loves", but not, intuitively, on the content of "neighbor" or "weigh".
The LOT hypothesis helps to explain how a physical system can implement systematic relations among attitudes, in much the same way that representationalism helps to explain the relations among different attitudes with the same content. For example, on the assumption that symbols have syntactic parts, it might be that two systematically related token attitudes physically overlap, i.e., share some of the same token parts.<15> Alternatively, such attitudes might contain tokens of a physical kind such that they can easily be reproduced from or matched against one another. This would allow the implementation of inferential processes such as variable-introduction and variable-binding which are sensitive to the syntactic structure of symbols, and are thereby sensitive to some of the semantic dependencies of the attitudes the symbols help to realize.<16>
In the mid-seventies, Fodor focused philosophical attention on the fact that nearly all existing models in cognitive science satisfy the language-of-thought hypothesis (and so, by implication, representationalism). Models of this sort have since become known as "classical" models. Although such models continue to dominate the field, from the earliest days of cognitive science various philosophers and scientists have found themselves dissatisfied with the classical framework as a whole. We can understand some of the phenomena which have seemed to cast doubt on classical models by focusing on a few striking facts about a certain sort of skill acquisition.
Novices at many activities (driving, playing basketball, delivering speeches, etc.) usually operate by deliberating-- by applying memorized rules and recipes (or, at least, rough, partial ones). Often, the novice's rules are of limited reliability and scope, and are applied slowly and haltingly, consciously and self-consciously. With routine practice, however, performance often improves dramatically. One can recognize more of the relevant aspects of what's happening, settle on better decisions in a wider range of situations, and execute those decisions more fluently even under duress. It therefore appears that the expert's inferential processes are somehow sensitive to vastly more conditions than are the novice's inferential processes. Paradoxically, these increases in what might be called "holistic sensitivity" are also accompanied by great increases in speed--the expert can do far more than the novice, but can do it far more quickly. This paradox has seemed to many to lead to a difficulty for classical models.
I have been portraying the classical framework as being motivated by a specific aspect of the mental-body problem: how can inferential processes be realized physically? The analogy with computers--as enshrined in the LOT hypothesis, for example--does appear to be a promising answer to this question. However, as the inferential processes are considered to be sensitive to more and more conditions, and to operate more and more quickly, critics of the classical framework have felt less and less sure of the computer analogy as an account of how such processes are to be implemented.<17> The worry needs to be formulated more carefully. Certainly present-day computers can store large numbers of symbols, and quickly access and transform them all. Similarly, classical theorists can appeal to analogies with ever-larger and ever-faster computers.
Since computers are physical, this strategy is relevant to the mental-body problem. Seen in a larger philosophical context, however, such a solution to the mental-body problem would be unsatisfying. We don't merely want to know how some physical system can implement mental processes (such as holistically sensitive inference). We want to know how we can do so, i.e., how it is possible for these processes to be implemented in brains. Call this the "mental-brain problem". We are especially interested in this problem not simply because we have a parochial interest in human cognition, as we might be especially interested in news from the old hometown. Rather, the special interest derives from the philosophical interest in assessing the fate of functionalism and token physicalism as answers to the mind/body problem. The mind/body problem is a problem about existing mental phenomena, including at the very least human mental phenomena. If functionalism and token physicalism cannot furnish answers to the mental-brain problem, then they cannot be general solutions to the mind/body problem.
Why should the mental-brain problem seem any more difficult than the mental-body problem? The worry only begins to take shape when we notice relevant differences between brains and supercomputers. Without entering into needless detail, the important point is that neurons are extremely slow in relation to the symbol-manipulating processes of familiar computers (even setting aside imaginary improved computers).<18> As a result, the aspect of the mental-brain problem having to do with the implementation of rapid, holistically sensitive inferential processes seems especially challenging. This is one of the central challenges the connectionist framework is meant to address. We will be better able to understand the potential difficulty for the classical framework if we introduce an alternative connectionist approach.
0.2 The Connectionist Framework
Before entering into a direct description of connectionist approaches to this issue, it is best separately to introduce a few key notions, and to consider standard sorts of connectionist models which are not centrally concerned with explaining holistically sensitive inference. Fortunately, the issues of present concern can be described without focusing on the fine details of connectionist networks. The most important idea is that of a node. Nodes are simple energy-transmitting devices which, in the simplest case, are characterized at a given time by their degree of activation, or propensity to affect other nodes. Nodes are connected to one another by stable energy conduits, by means of which active nodes tend to alter the activation of other nodes. (Finer details about these connections will turn out to be of no concern.) Although some nodes may have direct connections only to other nodes, others may interact with sensory or motor mechanisms, or (perhaps) with nonconnectionist cognitive mechanisms.
This specification of connectionist models makes no mention of mental phenomena, and so is silent on the question of functionalism and token physicalism about propositional attitudes. Indeed, it is possible to be a connectionist and deny that any propositional attitudes (whether of a sort familiar to common sense or of a sort to be discovered by scientific psychology) are realized in the models one adopts. Presumably, such a position would not respond to our latest outbreak of the mental-body problem--the question of how (rapid, holistically sensitive) inferential processes can possibly be implemented in brains. For this reason, there is special interest in connectionist theories which are coupled with a functionalist and token physicalist approach to propositional attitudes; I will limit my discussion to such versions of connectionism.
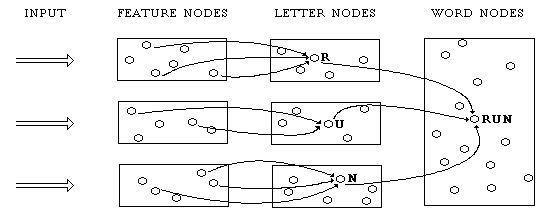
Where are the representations in connectionist models? On one conception, individual nodes are representations.<19> Perhaps the most famous example is the "interactive activation model" of reading (Rumelhart and McClelland, 1982). It may be pictured in part as in Figure 1. The network contains "word nodes" each of which standardly becomes activated as a result of the presentation of a particular word, and each of which represents the presence of that word. These word nodes are activated by "letter nodes" each of which represents and standardly responds to the presence of a particular letter at a particular position in the word. Finally, each letter node is activated by "feature nodes", each of which represents and standardly responds to the presence of a certain feature of the shape presented at a particular position: a horizontal bar, a curved top, etc.
Figure 1: Rumelhart and McClelland's (1982) interactive-activation model of reading.
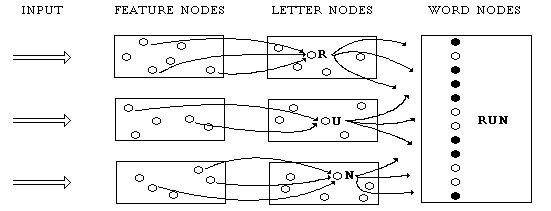
Individual nodes which serve as representations are called "local" representations, in contrast with "distributed" representations, which are patterns of activity of many nodes. For example, we can imagine a modification of the interactive activation model of reading, in which the presence of each word is represented not by an individual node, but by several nodes, as in Figure 2. Here the connections between the letter nodes and the nodes in the word patterns are arranged so that, for example, the letter nodes "R", "U", and "N" tend to activate all and only the nodes in the pattern which represents the presence of the word "RUN" (those darkened in Figure 2). On most distributed schemes of representation, representations overlap, that is, share nodes. In the present example, the word "ANT" might be represented by a pattern of activation which includes some of the same nodes as those in the pattern which represents "RUN". Similarly, we might imagine further modifications of the model in which the letter nodes are replaced by letter patterns, the feature nodes are replaced by feature patterns, and perhaps even the extreme case in which all the representations--for features, letters, and words--are patterns of activation defined over all the nodes in the model.
Figure 2: The interactive-activation model of reading modified to include distributed representations for words.
0.2.2 Connectionism and Representationalism
While it is clear that the most common and interesting sorts of connectionist networks are supposed to contain token propositional attitudes,<20> it is a tricky question whether any of these representations qualify as symbols rather than token attitudes, in the sense required by representationalism (see section 0.1.2). While the situation is bound to vary from model to model, reflection on certain fairly standard features of the (real and imagined) reading models seems to suggest that most familiar connectionist models are supposed to adhere to representationalism.
As a preliminary consideration, connectionists normally attribute content to (groups of) nodes in such models. Since (groups of) nodes are ordinary objects rather than occurrences, they cannot be token attitudes, and so (by a process of admittedly nondemonstrative elimination) must be ideas or symbols. Of course, it is possible to object that this talk is merely sloppy, and that the only representations are states of activation of the nodes, which do stand a chance of being identical to token attitude states. Intuitively, the models "cognize" that the word "RUN" is present only when the appropriate nodes are activated, so there is support for the view that only activation states are representations. Nevertheless, I think there is a point to considering the nodes themselves to be representations. The point is that these nodes appear to play the functional and explanatory role of ideas, and so (by functionalism) they must be ideas.
Consider first that the models are capable of entering into a variety of attitudes with the same content, e.g., that the word "RUN" is present. Some states of the "RUN" nodes play a functional role akin to that of forming a hypothesis, while other states of the same nodes play a role akin to that of concluding. There are a wide range of intermediate attitudes as well. The nodes themselves are common parts of these various attitudes, just as a token idea is typically involved in many different token attitudes with the same content. The nodes therefore afford a physical explanation of the special causal relations among these different attitudes, in precisely the sense in which ideas are supposed to explain these relations. Furthermore, like token ideas, the nodes persist through changes in the corresponding attitudes, and may exist without the presence of any corresponding attitude. I suggest that these considerations make plausible the claim that standard connectionist models adhere to representationalism, and that typically (groups of) nodes are token ideas and symbols. If this is right, the relation of connectionist models to the classical framework appears to turn on whether they adhere to the language-of-thought hypothesis, and in particular on whether they support syntactically complex symbols.<21> This will be the main focus of chapter 1.
0.2.3 Connectionism and Holistically Sensitive Inference
We are now in a position to consider how the connectionist framework affords strategies for solving our specific version of the mental-brain problem: how can rapid, holistically sensitive inferential processes be realized by physical relations between slow (at least by current technological standards) neuron-like elements? Recall that an inferential process is holistically sensitive to the extent that it depends on a wide range of conditions. Experts at various skills--auto racing, basketball, conversation, etc.--appear to engage in processes which are sensitive to an indefinitely wide range of conditions, and do so in "real time", even in fractions of a second. A cognitive system with an unimaginably fast processor might duplicate this performance by considering each condition in turn, assessing the relevance of each to the inferential task at hand (possibly making several "passes"), and then drawing the appropriate inferences. However, this strategy is unavailable for us, on the assumption that our processors are (relatively slow) neurons.
The connectionist framework makes available two strategies for minimizing the time necessary to engage in holistic processes within the limits of neuron-like processors. The first strategy is massively parallel processing. If many conditions relevant to an inference can be considered at the same time, by separate processors, the total time needed for the inference may be decreased substantially. The second strategy is the avoidance of syntactic complexity. It appears likely that syntactically complex representations place a heavier computational burden on processors than syntactically simple representations do. For this reason, if conditions relevant to an inferential process can be adequately represented by syntactically simple representations, the time it takes to consider each condition is reduced.
These ideas are illustrated in a partial connectionist theory of skill due to Philip Agre (Agre, 1989). On Agre's theory, well-practiced, routine activity is guided by an enormous "dependency network", each node of which corresponds to a potential belief, desire, or other propositional attitude of the agent. The agent has the attitude when the node is activated, and doesn't have it when the node is inactivated. The network is connected in such a way that the nodes activate and deactivate each other in "mimicry" of inferential arguments which were previously generated (presumably) by the relatively long, drawn out calculations of a more flexible mechanism (e.g., the novice's conscious trial-and-error search). The circuitry allows hundreds or thousands of these "arguments" to take place in massive parallel and at blinding speed. As Agre describes the system, it "is continually redeciding what to do insofar as the circuitry produces a fresh set of decisions about action many times a second" (Agre, 1989, p. 139).<22>
Like many others, I find models within both the connectionist framework (such as dependency networks) and the classical framework (such as production systems--see section 0.2.3) attractive in accounting for inferential processes. One underlying aim of my thesis is to get us closer to the goal of deciding between these models, or between their relatives (although I regret to say that my conclusions leave us very far from this goal). The thesis addresses three specific issues raised by philosophers interested in the emerging debate between the classical and connectionist frameworks.
Fodor's contention in The Language of Thought (Fodor, 1975) was that, whatever the fate of particular existing models of cognition, the language-of-thought hypothesis must be satisfied by any adequate model. Those who wished to resist this conclusion were especially hampered by the fact, repeatedly stressed by Fodor, that no serious alternatives to LOT models had ever been proposed. Today, however, with the advent of connectionist models, many people at last see promise of a plausible way to avoid commitment to the LOT hypothesis. This is where the fun starts. Fodor stands his ground; along with Zenon Pylyshyn, he argues that connectionist models which fail to implement a language of thought also fail to account for certain fundamental aspects of cognition, and in particular "systematic" relations among propositional attitudes akin to those with which I began section 0.1.3. Some critics, most notably Paul Smolensky (1989), have tried to provide counterexamples to this conclusion.
In chapter 1, I will display the failings of Fodor and Pylyshyn's argument which make these counterexamples initially plausible, but I will also argue that Fodor and Pylyshyn's conclusion withstands the alleged counterexamples. This issue is relevant to whether models of skill such as Agre's dependency networks can be modified so as to account for systematic relations among attitudes without adopting the LOT hypothesis and falling within the classical framework.
My concern in chapter 2 is to address a puzzle about the content of representations in certain connectionist models, such as the interactive activation model of reading and Agre's dependency networks. The puzzle arises within particular philosophical views of content, versions of what I will call the "fine-grained theory". According to these views, contents admit of degrees of complexity. Even the simplest propositions (e.g., the proposition that a is F) are thought to be complexes of constituent concepts (e.g., the concepts a and F). What is required for a representation r to have a complex content, say, the proposition that a is F? On the fine-grained theory, as I will construe it, r must display "semantic dependence" on other representations of the concepts a and F, i.e., the constituent concepts of the proposition. What sort of relation between representations counts as semantic dependence? The most familiar examples are syntactic relations: the content of the English sentence "sugar is white" depends on the content of its syntactic parts "sugar" and "white". Another example of semantic dependence might loosely be termed "abbreviation": a syntactically simple representation "p" in a logical formalism may have a complex, propositional content in virtue of being treated (by convention or otherwise) as "standing in place of" a sentence such as "sugar is white", and so depending semantically on the parts of that sentence.
Although virtually all nonconnectionist models in cognitive science, as well as many connectionist models, postulate relations such as syntactic complexity and abbreviation, many connectionist models, including dependency networks and the reading model, appear not to support these relations. Nevertheless, for reasons I will describe there is at least an appearance that representations in these models do have propositional contents. This generates a philosophical puzzle, at least for those sympathetic to the fine-grained theory of content: how it is possible for a representation to have propositional content without displaying semantic dependence on other representations (e.g., without being either syntactically complex or an abbreviation)? My goal in chapter 2 is to explain how.
In my discussion of holistically sensitive inference, I have considered a kind of brute-force approach: that such inferential processes do access a large number of representations, and that the main problem is to show how a system can maximize the number of representations which can be accessed in a short amount of time. While massive parallelism and avoidance of syntactic complexity are effective techniques for increasing speed, they (especially the latter) suffer from serious computational deficiencies (of the sort described in chapter 1). It therefore appears that we need an alternative to the brute-force approach; in particular, we need to develop processing strategies which minimize the number of representations which need to be accessed in implementing a given inferential process.
We can begin by noticing two senses in which an inferential process can be sensitive to a condition, and so two senses of "holistically sensitive inference". An inferential process can be sensitive to a condition in the sense that it always operates by accessing a representation of that condition, or it can be sensitive in the sense that it has potential access, when necessary, to the representation. Although it is clear that expert activity is sensitive to a wide range of conditions, it is unclear in which sense this is so.
If the expert's increased holistic sensitivity consists of accessing far more representations than novices access, then the increased speed associated with expertise is paradoxical, and a brute force approach involving connectionist technology may appear inevitable. If, instead, the increased holistic sensitivity consists in an increased range of representations which the expert can access only when necessary, then we can even begin to explain the increased speed. Perhaps the expert can avoid continually accessing representations which the novice continually has to access, because the expert has a better ability to "tell" when they are irrelevant to the activity. While cognitive scientists, particularly those studying artificial intelligence, have tried to develop algorithms for modeling such an ability, several philosophers have tried to portray one or another version of the "frame problem" as principled objections to these strategies.
The frame problem is widely reputed among philosophers to be one of the deepest and most difficult problems of cognitive science. Chapter 3 discusses three recent attempts to display this problem: Dennett's problem of ignoring obviously irrelevant knowledge, Haugeland's problem of efficiently keeping track of salient side effects of occurrences, and Fodor's problem of avoiding the use of "kooky" concepts. In a negative vein, I argue that these problems bear nothing but a superficial similarity to the frame problem of AI, so that they do not provide reasons to disparage standard attempts to solve it. More positively, I argue that these problems are easily solved by slight variations on familiar AI themes. Finally, I devote some discussion to more difficult problems confronting AI. If the arguments I provide are correct, then we may not need to abandon classical models (or abandon classical features in connectionist models) in explaining how rapid, holistically sensitive inference can be implemented with processors as slow as neurons.
In this chapter I have tried to do two things: (1) display classical and connectionist models as responses to questions raised by a functionalist and token physicalist approach to the mind/body problem, and (2) display a substantive dispute between classical and (certain) connectionist models of inferential processes in skills. When I have completed my discussions of the language-of-thought hypothesis, fine-grained theories of content, and the frame problem, how will the models appear to stand with respect to skills and the mind/body problem? I don't know, to be honest. I will not be presenting an argument to the effect that one of the models is better than the other with respect to skills. At best, I will be trying to remove certain difficulties with interpreting these models, and trying to locate the theoretically interesting differences between them, so that we have a better chance of testing them against facts about skills. Nor will I be presenting an argument to the effect that either framework is likely to solve the mental-brain problem, and so I will not be taking a stand on the likelihood that functionalism and token physicalism solve the mind/body problem. At best, I will have cleared away some apparent difficulties for these models, and will have brought other difficulties into sharper focus.
NOTES
<1>I will usually use the term "occurrence" as a general term for anything that occurs or happens, including events and states (and also facts, situations, conditions, etc.). From the standpoint of functionalism, the interesting feature common to all occurrences is that they may enter into causal relations. I mean to abstract away from more detailed claims about the individuation of these phenomena, e.g., that a token event of stabbing Caesar can be identical to a token event of killing Caesar, or that a token state of stabbing Caesar cannot be identical to a token state of killing Caesar (for discussion, see Davidson, 1969).
<2>Unless otherwise mentioned, I follow the standard practice of construing "physical" broadly, to cover not only the entities mentioned in the theories of physics, but also any natural (as opposed to supernatural), nonmental, spatiotemporal phenomena.
<3>This position is distinguishable from (though compatible with) "type physicalism", which identifies M with some physical state or event type B to which all tokens of M belong. For discussion, see the related articles in Block, 1980.
<4>This should not be confused with the problem of "interaction": how is it possible for physical states or events to enter into causal relations with mental states or events? Interaction is only a problem for theories which, unlike token physicalism, treat token mental occurrences as nonphysical. In short, the question is not about how it is possible for a body to interact with the mental, but is instead about how it is possible for a body to be mental. Hence the name "mental-body problem" (with a dash) rather than "mind/body problem" (with a slash). It bears emphasis that the mental-body problem must be solved in order for functionalism and token-physicalism to work as a solution to the mind/body problem.
<5>I do not make the assumption that all propositional attitudes are familiar to common sense, since scientific psychology may well discover new sorts.
<6>It matters that the attitude-types listed above are such that we can have a token of any one type without also having a token of another type. By comparison, presumably there is no mystery as to how a physical system which can know that p can also manage to believe that p.
<7>This inference depends on certain assumptions about what it is for a thinker to stand in a computational relation to a representation, but these assumptions are natural and (as far as I know) never called into question by representationalists. To a near-enough approximation, we may understand computation as a process of using representations as premises or conclusions of inferential processes. In this way, it appears, we can at least make sense of a representation's bearing a computational relation to other representations--namely, those for which it is used as a (co)premise or (co)conclusion. By a slight extension, we may imagine that representations also stand in computational relations to the inferential processes which act upon them. But what is it for a representation to stand in a computational relation to a thinker? The only natural account I can think of is that a thinker has a computational relation to a representation if and only if that representation has a role in the thinker's inferences. Given this, the inference in the text is correct.
<8>Strictly speaking, r can be the having-of-an-idea that p, i.e., a certain kind of representational state or event with the content that p. I will use "idea" in a broad sense, namely, as being neutral with respect to the object/occurrence distinction. It is sometimes suggested that representationalism requires representations to be ordinary objects (things that exist but do not happen) rather than occurrences (things that do happen). For reasons given below, I want to reject this proposed requirement. Although "idea" seems to be the best word for expressing representationalism, it may misleadingly bias one towards the requirement. While I admit that it seems unnatural to say that ideas happen, I am inclined to treat this as having minuscule ontological import. To take an analogous case, it seems equally unnatural to say that representations happen, although it is proper to say that representational occurrences (e.g., an assertion that sugar is white) are representations.
The proposed requirement of representational objects has other, nongrammatical sources of support. First, it would be sufficient to distinguish representationalism from token physicalism, since token physicalism about propositional attitudes is committed only to the existence of representational physical states or events, and not to the existence of representational physical objects. The requirement also derives some plausibility from the claim that propositional attitudes are realized as relations between thinkers and representations; it is most natural to think of relations as holding between ordinary objects. An analogy with natural language also lends support to the requirement, since languages include representational objects such as sentences.
Nevertheless, the requirement is too strong. It is perfectly possible for there to be computational relations between thinkers and occurrences. Just as a speaker can draw a conclusion from a sentence (a kind of ordinary object), so can he draw a conclusion from an utterance (a kind of occurrence). For analogous reasons, little of computational interest seems to hang on whether mental representations are realized as, say, neurons (objects) or as, say, the firings of neurons (occurrences). Indeed, any apparent importance of the object/occurrence distinction vanishes when we compare treating an object as a representation with treating the existence of the object as a representational state. Finally, we can insure the distinction between representationalism and token physicalism by simply denying that ideas are propositional attitude occurrences, without denying that they are occurrences of some other sort.
<9>As I will explain in a moment, it is this claim, coupled with token physicalism about ideas, which advances us toward the goal of solving the special case of the mental-body problem with which we began this section, namely, the problem of explaining how a physical system can implement systematic causal relations among different attitudes that p.
<10>What is less clear is whether there is any way to distinguish inferential relations from non-inferential relations among representations (e.g., association of propositional ideas), short of appealing to the rationality values of the representations. I will return to this point in section 2.2.1, where I will also criticize alternative accounts of the difference between attitudes and ideas.
<11>Since I will often employ the notion of symbols illustrated in this paragraph, I would like to call attention to a few features of my use of the word. Although there is a perfectly useful sense in which anything with content is a symbol, I will usually subject this term to a number of restrictions. First, unless otherwise clear from the context I will usually reserve the word "symbol" for mental symbols--i.e., symbols which help to realize propositional attitudes--rather than natural-linguistic or other nonmental symbols. Furthermore, when there is a danger of confusion between token attitudes and token ideas (and there usually is), I will reserve the word "symbol" for physical structures related to the latter (either by identity or by reproduction, as illustrated in the text). Given this usage, although functionalism and token physicalism about propositional attitudes are committed to the existence of mental representations, they are weaker than representationalism in not being committed to the existence of mental symbols. (While this distinction can be expressed in terms of ideas, "symbol" emphasizes the physical nature of the structures involved, and also allows me to ignore differences between the two sorts of physical realizations of ideas mentioned in the text.) Finally, "symbol" (like "idea" and "representation") is neutral with respect to the object/occurrence distinction (see note <8>).
<12>To avoid repeated use of the modifier "syntactic", I will often speak of "complexity" and "simplicity" intending the modifier to be understood.
<13>Although there may be viable but weaker conceptions of syntactic complexity according to which syntactic constituents do not need to be parts of complex symbols, Fodor is emphatic that parthood is required for a language of thought. He insists repeatedly that the LOT hypothesis claims that "(some) mental formulas have mental formulas as parts" (Fodor, 1987a, p. 137), and that this notion of parthood is literal:
Real constituency does have to do with parts and wholes; the symbol 'Mary' is literally a part of the symbol 'John loves Mary'. It is because their symbols enter into real-constituency relations that natural languages have both atomic symbols and complex ones. (Fodor and Pylyshyn, 1988, p. 22)
<14>If (some) mental symbols are physical occurrences rather than ordinary physical objects, then the LOT hypothesis demands a notion of spatiotemporal parthood for (token) occurrences as well as for (token) individuals. There is some leeway in the construction of such a notion. I will illustrate the tactics available for the case of states, conceived of as instantiations of properties by objects. (I will have to leave open the question of whether a similar account can be given for other sorts of occurrences, such as events.) One intuitively plausible idea is that a state P is a part of a state W iff P is a logically necessary condition of W. This might serve to capture the intuitively important fact that parts, taken together, constitute wholes, so that the existence of a whole depends upon that of its parts. For example, let S be the state of neuron n's firing at t, and let S' be the state of n's firing and having a high threshold at t. On this account of parthood for states, S is a part of S'.
While this may seem roughly right as an account of state-parthood in general, the notion of syntactic complexity which it generates is, I think, too weak. As I will explain in section 1.2.4, given this notion of a syntactic state-part, one can literally prove the existence of syntactic complexity (and so, nearly enough, the truth of the LOT hypothesis) from the nearly indisputable premise that there is some explanation or other which is common to one's ability to engage in a range of semantically related inferences (see Davies, 1990). This would make the LOT hypothesis virtually impossible to reject (without also rejecting, say, token physicalism about propositional attitudes).
To avoid this result, we need to motivate a stronger constraint on syntactic parthood than that suggested by the current account of state-parthood. I think that this account leaves out the spatiotemporal aspects of syntactic parthood which are intuitively important for the LOT hypothesis. Suppose, as seems natural, that a state is where the individuals which "participate" in the state are. (Where did Mary hug John? Wherever Mary and John were, of course. But see section 1.2.4 for criticism of this as a general account of state-locations.) Then state S is not a spatiotemporally proper part of state S', since their spatiotemporal locations coincide. If, as I am suggesting, a reasonably strong LOT hypothesis postulates that some mental symbols are spatiotemporally proper parts of other mental symbols, then I don't think we should count such conjuncts as candidate syntactic parts. Rather, a state P is a spatiotemporally proper part (and so a candidate syntactic part) of a state W only if (i) P is a necessary condition for W and (ii) P's location is properly within W's location. For example, state S is a spatiotemporally proper part of the following two states: (a) neuron n and neuron m's firing at time t, and (b) n's firing at t and t'.
I will return to these points in section 1.2.4, where I attempt to show that fully-fledged spatiotemporal complexity is necessary to explain the range of phenomena typically taken to be explained by the LOT hypothesis.
<15>This is the case with certain semantic (or propositional) networks of the sort often contained in traditional cognitive-scientific models (for a review, see Johnson-Laird, et al., 1984). In such a network, nodes are symbols for objects and properties (among other things), and pieces of the network (i.e., groups of nodes along with their connections) are symbols which help to realize attitudes. Groups of attitudes (thought to be) about the same thing (e.g., toothpaste) typically share a node representing that thing. This allows mechanisms easily to implement inferential relations among these attitudes.
<16>This sort of matching occurs, for example, in "production system" models (see Anderson, 1983; Holland, et al., 1986). In these models, a thinker's thoughts and goals are realized by storing syntactically complex symbols in various buffers, including long-term and working memory, where they may be acted upon by inferential processes. Some of these inferential processes are realized by special kinds of "IF...THEN..." rule-symbols called "productions". Although details vary from theory to theory, a production may be thought of as a rule-symbol with a (tiny) processor. The processor's task is to watch out for the presence of a symbol matching its "IF" part (modulo differences between variables and constants), and to perform some simple action corresponding to its "THEN" part, such as forming a copy of the "THEN" part in working memory (perhaps with variables bound or introduced). It is as if one could write a conditional sentence in a book, give it tiny eyes and arms, and give it one reflex: when you see a copy of your "IF" part written somewhere, write down a (possibly modified) copy of your "THEN" part (or do something comparably simple). With the use of variables, a single production (e.g., "IF x is white, THEN x is not yellow") can implement systematic causal relations among a wide range of pairs of token attitudes which have parts of a single physical type (e.g., the beliefs that toothpaste is white and that toothpaste is not yellow, the desires that teeth are white and that teeth are not yellow, etc.).
<17>These objections to the classical model should not be confused with considerably weaker objections which appeal to unconscious processing or processing without rule-symbols. Notoriously, the expert's improvements over the novice with respect to holistic sensitivity and speed coincide with--and seem to require--a reduction in the conscious application of rule-symbols. But it is not a necessary feature of classical models that processes should be conscious, nor even that they should be realized by rule-symbols.
<18>Here are the numbers as reported by a trio of highly influential connectionists:
Neurons operate in the time scale of milliseconds whereas computer components operate in the time scale of nanoseconds--a factor of 106 faster. This means that human processes that take on the order of a second or less can involve only a hundred or so time steps. (Rumelhart, et al., 1986, p. 75)
The appeal to neurons is necessary to motivate the worry, since a classical theorist can point out that some physical processes in brains-- e.g., quantum-mechanical ones--are fast even in relation to the symbol-manipulating processes in present-day computers. It is an interesting question why physicalists are loathe to postulate that token mental occurrences are much "smaller" than neurons. Robert Cummins offers the plausible argument that doing so would deprive us of an explanation of the biological inheritance of mental properties, since (as far as we know) it is only roughly cell-sized features which are determined by genes (Cummins, 1983, pp. 63-65).
<19>Connectionists often fail to be explicit about whether the representations are nodes themselves, or rather states of nodes (such as activation levels). I will discuss this distinction in the next section, while discussing the relation between connectionism and representationalism. For now, when I speak of a node as a representation, this can be taken as a simplified way of speaking of a node or one of its states as a representation. The same simplification applies to talk of groups of nodes as representations.
<20>This is only "clear" if we do not limit the class of propositional attitudes to those which are familiar from commonsense, and if we ignore claims of the sort that genuine propositions can only be represented by (say) syntactically complex representations. The latter sort of claim receives extended discussion in chapter 2.
<21>At any rate, most connectionist critics of the classical framework set up the issue specifically in terms of syntactic complexity.
<22>Although Agre's dependency networks rely almost exclusively on local schemes of representation (one representation per node), analogous models are possible which make more use of distributed symbols. Such alternatives can decrease the number of nodes required of a network, and can increase its reconfigurability (ability to change which symbols affect which other symbols), but at the cost of decreased speed.
REFERENCES
Agre, P., 1989: "The Dynamic Structure of Everyday Life", Ph.D. thesis, MIT A.I. Lab.
Anderson, J., 1983: The Architecture of Cognition, Harvard University Press, Cambridge.
Armstrong, D., 1983: What Is a Law of Nature?, Cambridge University Press, Cambridge.
Barr, A., and E. Feigenbaum, ed., 1981: The Handbook of Artificial Intelligence, vol. I, William Kaufmann, Inc., Los Altos, CA.
Barwise J., and J. Perry, 1981: Situations and Attitudes, MIT Press, Cambridge.
Benacerraf, P., 1965: "What Numbers Could Not Be", Philosophical Review.
Block, N., ed., 1980: Readings in Philosophy of Psychology, Harvard University Press, Cambridge.
Block, N., 1986: "Advertisement for a Semantics for Psychology", in Midwest Studies in Philosophy, vol. 9.
Carnap, R., 1947: Meaning and Necessity, University of Chicago Press, Chicago.
Chalmers, D., 1990: "Why Fodor and Pylyshyn Were Wrong: The Simplest Refutation", manuscript.
Clark, A., 1989: Microcognition, MIT Press, Cambridge.
Cresswell, M., 1985: Structured Meanings, MIT Press, Cambridge.
Cummins, R., 1983: The Nature of Psychological Explanation, MIT Press, Cambridge.
Cummins, R., and G. Schwarz, 1987: "Radical Connectionism", Southern Journal of Philosophy (supplement).
Cummins, R., 1989: Meaning and Mental Representation, MIT Press, Cambridge.
Davidson, D., 1969: "The Individuation of Events", in Essays on Actions and Events, Oxford University Press, Oxford, 1980.
Davidson, D., 1975: "Thought and Talk", in Inquiries into Truth and Interpretation, Oxford University Press, Oxford, 1984.
Davies, M., 1989: "Concepts, Connectionism, and the Language of Thought", Proceedings of the International Colloquium on Cognitive Science.
Dennett, D., 1984: "Cognitive Wheels: the Frame Problem of AI", in Pylyshyn, ed., 1987.
Dennett, D., 1983: "Styles of Mental Representation", in The Intentional Stance, MIT Press, Cambridge, 1987.
Dretske, F., 1977: "The Laws of Nature", in Philosophy of Science.
Dreyfus, H., 1979: What Computers Can't Do, Harper Books, New York.
Dreyfus, H. and S. Dreyfus, 1986: Mind Over Machine, Free Press, New York.
Evans, G., 1983: The Varieties of Reference, Oxford University Press, Oxford.
Fikes, R., and N. Nilsson, 1971: "STRIPS: A New Approach to the Application of Theorem proving to Problem Solving", Artificial Intelligence.
Fodor, J., 1968: "The Appeal to Tacit Knowledge in Psychological Explanations", in Fodor, 1981.
Fodor, J., 1975: The Language of Thought, Harvard University Press, Cambridge.
Fodor, J., 1981: Representations, MIT Press, Cambridge.
Fodor, J., 1983: The Modularity of Mind, MIT Press, Cambridge.
Fodor, J., 1987a: "Why There Still Has to be a Language of Thought", in Psychosemantics, MIT Press, Cambridge.
Fodor, J., 1987b: "Modules, Frames, Fridgeons, Sleeping Dogs, and the Music of the Spheres", in Pylyshyn, ed., 1987.
Fodor, J. and Z. Pylyshyn, 1988: "Connectionism and Cognitive Architecture", in Cognition.
Goodman, N., 1965: Fact, Fiction, and Forecast, Bobbs-Merrill, Indianapolis.
Haugeland, J., 1985: Artificial Intelligence: the Very Idea, MIT Press, Cambridge.
Haugeland, J., 1982: "The Nature and Plausibility of Cognitivism", in The Behavioral and Brain Sciences.
Haugeland, J., 1987: "An Overview of the Frame Problem", in Pylyshyn, ed., 1987.
Hayes, P., 1987: "What the Frame Problem Is and Isn't", in Pylyshyn, ed., 1987.
Holland, J., K. Holyoak, R. Nisbett, and P. Thagard, 1986: Induction, MIT Press, Cambridge.
Janlert, L., 1987: "Modeling Change--The Frame Problem", in Pylyshyn, ed., 1987.
Johnson-Laird, P., D. Herrmann, and R. Chaffin, 1984: "Only connections: A critique of semantic networks", Psychological Bulletin.
Lewis, D., 1972: "General Semantics", in Philosophical Papers, v. 1, Oxford University Press, Oxford.
McCarthy, J., and P. Hayes, 1969: "Some Philosophical Problems from the Standpoint of Artificial Intelligence", in B. Meltzer and D. Michie, eds., Machine Intelligence 4, Edinburgh University Press, Edinburgh.
Preston, E., 1988: "Representational and Non-Representational Intentionality", Ph.D. thesis, B.U. Philosophy Dept.
Pylyshyn, Z. (ed), 1987: The Robot's Dilemma: the Frame Problem in Artificial Intelligence, Ablex, Norwood, NJ.
Rumelhart D., and J. McClelland, 1982: "An interactive activation model of context effects in letter perception", in Psychology Review.
Rumelhart D., G. Hinton, and J. McClelland, 1986: "A General Framework for Parallel Distributed Processing", in J. McClelland and D. Rumelhart, ed., Parallel Distributed Processing, v. 1, MIT Press, Cambridge.
Searle, J., 1983: Intentionality, Cambridge University Press, Cambridge.
Schwarz, G., 1987: "Explaining Cognition as Computation", M.A. Thesis, University of Colorado Philosophy Dept.
Shoham, Y., 1988: Reasoning about Change, MIT Press, Cambridge.
Singley, M., and J. Anderson, 1989: The Transfer of Cognitive Skill, Harvard University Press, Cambridge.
Smolensky, P. 1988: "On the Proper Treatment of Connectionism", in The Behavioral and Brain Sciences.
Smolensky, P. 1989: "Connectionism, Constituency, and the Language of Thought", manuscript.
Stabler, E. 1983: "How Are Grammars Represented?", in The Behavioral and Brain Sciences.
Stalnaker, R. 1984: Inquiry, MIT Press, Cambridge.
Stich, S. 1984: From Folk Psychology to Cognitive Science, MIT Press, Cambridge.
Tooley, M. 1989: Causation, Cambridge University Press, Cambridge.
van Gelder, T. 1989: "Compositionality: Variations on a Classical Theme", manuscript.