University of Michigan
lormand@umich.edu
September, 1991
Fodor and Pylyshyn (1988) have presented an influential argument to the effect that any viable connectionist account of human cognition must implement a language of thought. Their basic strategy is to argue that connectionist models that do not implement a language of thought fail to account for the systematic relations among propositional attitudes. Several critics of the LOT hypothesis have tried to pinpoint flaws in Fodor and Pylyshyn’s argument (Smolensky 1989; Clark, 1989; Chalmers, 1990; Braddon-Mitchell and Fitzpatrick, 1990). One thing I will try to show is that the argument can be rescued from these criticisms. (Score: LOT 1, Visitors 0.) However, I agree that the argument fails, and I will provide a new account of how it goes wrong. (The score becomes tied.) Of course, the failure of Fodor and Pylyshyn’s argument does not mean that their conclusion is false. Consequently, some connectionist criticisms of Fodor and Pylyshyn’s article take the form of direct counterexamples to their conclusion (Smolensky 1989; van Gelder, 1990; Chalmers, 1990). I will argue, however, that Fodor and Pylyshyn’s conclusion survives confrontation with the alleged counterexamples. Finally, I provide an alternative argument that may succeed where Fodor and Pylyshyn’s fails. (Final Score: LOT 3, Visitors 1.)
1 Ultralocal Connectionism and the LOT Hypothesis
The point of this section is to set out the dispute between the LOT hypothesis and certain forms of connectionism, particularly "ultralocal" connectionist models that contain only individual nodes as representations. First I describe the language-of-thought hypothesis (section 1.1) and ultralocal connectionism (section 1.2). Then I present and defend Fodor and Pylyshyn’s argument as applied to these models (section 1.3).
1.1 What is a language of thought?
The language-of-thought hypothesis is a claim about the physical realizations of propositional attitudes. It is a specific version of representationalism, which is the claim that propositional attitudes are (at least typically) physically realized as computational relations between thinkers and mental symbols that represent the propositions.<1> The LOT hypothesis goes one step beyond representationalism. According to the LOT hypothesis, the physical symbols postulated by representationalism admit of syntactic complexity. What is it for a symbol to be complex?<2> Although this is a very difficult question, we can operate with an intuitive idea, leaving technicalities aside.<3> The prototypical complex symbols are written sentences and phrases in natural language. Each complex sentence and phrase has two or more symbols--e.g., words--as spatiotemporally proper parts, where parthood is taken quite literally (that is, as the phenomenon studied in mereology). Accordingly, syntactically complex mental symbols are thought to have other mental symbols as literal parts.<4> The parthood may be spatial, as with written sentences, or temporal, as with spoken sentences, or a mixture of the two.<5>
In addition to the requirement of symbolic parts, a semantic requirement is standardly placed on syntactic complexity. Not only do sentences and phrases have other phrases and words as parts, but they also bear some sort of close semantic relation to these parts. Fodor and Pylyshyn express this relation by saying that "the semantic content of a [complex] representation is a function of the semantic contents of its syntactic parts, together with its constituent structure" (Fodor and Pylyshyn, 1988, p. 12). In other words, without delving into too many technicalities, the content of the complex symbol must depend on the contents of its parts, as the content of "Mary loves John" depends on the content of "loves," but not, intuitively, on the content of "neighbor" or "weigh."<6>
It might be worth pointing out a few things that the LOT hypothesis does not require. It does not say that all mental symbols are syntactically complex. Nor does it say that there are syntactically complex symbols in every natural "faculty" of the mind: it would be consistent with the LOT hypothesis for there to be no complex symbols in (say) the olfactory and motor systems, so long as there are complex symbols elsewhere in the mind. This raises the question: how many syntactically complex symbols are needed to establish the truth of the LOT hypothesis? We should not consider the LOT hypothesis true of a mental life that contains only one complex symbol, buried under a sea of noncomplex symbols. On the other hand, there is no precedent for any requirement to the effect that a certain minimum percentage of mental symbols must be complex.
To make the LOT hypothesis into an interesting psychological hypothesis, I will construe it as going one step beyond the requirement of syntactic complexity. A common understanding of the LOT hypothesis can be captured intuitively by the claim that the expressive power of a language of thought is at least as extensive as the expressive power of natural languages.<7> To a first approximation, this means that any content possessed by complex natural-linguistic symbols also can be possessed by complex mental symbols.<8> Without going into too many technicalities, this claim needs to be restricted. The language-of-thought hypothesis doesn’t (by itself) require that everyone’s language of thought must at each stage of their development contain symbols corresponding to all possible natural-linguistic symbols. While Fodor has defended something like this extremely strong claim, he has never treated it as part of the LOT hypothesis itself. Instead, I will suppose that for the LOT hypothesis to be true, any content possessed by complex natural-linguistic symbols comprehensible to a thinker at a time also can be possessed by complex mental symbols available to that thinker at that time.
Although the language-of-thought hypothesis goes beyond the syntactic complexity requirement, it is this requirement that has stimulated the most influential connectionist attacks. Accordingly, my focus in the rest of this paper will be on syntactic complexity. I will only address criticisms of Fodor and Pylyshyn that at least implicitly begin with the assumption of representationalism, and I will ignore issues of expressive power.
It is important to distinguish the general language-of-thought hypothesis from hypotheses about particular implementations of languages of thought. There are many different cognitive models in existence that implement languages of thought, including several dozen versions of production systems, and several dozen versions of "logic-based systems."<9> The language-of-thought hypothesis does not require that any particular one of these traditional models applies to human cognition. It doesn’t even require any of these models to apply, since it may be possible to invent new LOT models that differ in cognitively interesting ways from traditional ones. Indeed, if the arguments I will give below are correct, some of the most interesting connectionist models qualify as "new" LOT models. To be clear, then, we must distinguish two questions that may be asked about a given connectionist model:
(1) Does the model implement a language of thought?
(2) Does it implement some (or any) particular preconceived implementation of a language of thought (such as production system X)?
I construe Fodor and Pylyshyn as arguing that the answer to question (1) is likely to be "yes" for any potentially plausible connectionist models.<10> Fodor has a special stake in question (1), since he wants to defend the LOT hypothesis from philosophers who have sought to use connectionism against it. It is less clear that Fodor has any special stake in question (2): he is, after all, a notoriously vehement critic of traditional cognitive-scientific models, especially those rooted in artificial-intelligence research.<11> In the rest of this paper, then, I will be concerned only with question (1), as it arises with respect to various connectionist models. Before entering into a direct description of Fodor and Pylyshyn’s arguments on this score, however, it is best separately to introduce a few key connectionist constructs.
Fortunately, the issues of present concern can be described without focusing on the fine details of connectionist networks. The most important idea is that of a node. Nodes are simple energy-transmitting devices, which in the simplest case are characterized at a given time by their degree of activation, or propensity to affect other nodes. Nodes are connected to one another by stable energy conduits, by means of which active nodes tend to alter the activation of other nodes. (Finer details about these connections will turn out to be of no concern.) Although some nodes may have direct connections only to other nodes, others may interact with sensory or motor mechanisms, or (perhaps) with nonconnectionist cognitive mechanisms.
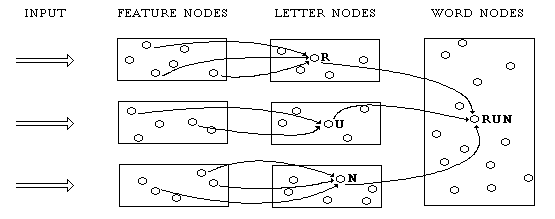
Where are the representations in connectionist models? On one conception, individual nodes (or states of individual nodes) are representations. Perhaps the most famous example is the "interactive activation model" of reading (Rumelhart and McClelland, 1982). It may be pictured in part as in Figure 1. The network contains "word nodes" each of which standardly becomes activated as a result of the presentation of a particular word, and each of which represents the presence of that word. These word nodes are activated by "letter nodes" each of which represents and standardly responds to the presence of a particular letter at a particular position in the word. Finally, each letter node is activated by "feature nodes," each of which represents and standardly responds to the presence of a certain feature of the shape presented at a particular position: a horizontal bar, a curved top, etc.
Figure 1: Rumelhart and McClelland’s (1982) interactive-activation model of reading.
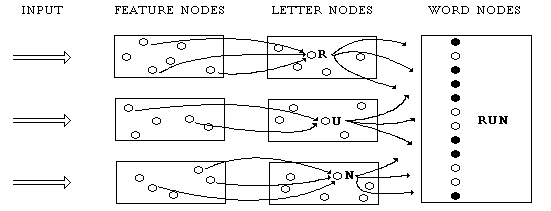
Individual nodes that serve as representations are called "local" representations, in contrast with "distributed" representations, which are patterns of activity of many nodes. For example, we can imagine a modification of the interactive activation model of reading, in which the presence of each word is represented not by an individual node, but by several nodes, as in Figure 2. Here the connections between the letter nodes and the nodes in the word patterns are arranged so that, for example, the letter nodes "R," "U," and "N" tend to activate all and only the nodes in the pattern that represents the presence of the word "RUN" (those darkened in Figure 2). On most distributed schemes of representation, representations overlap, that is, share nodes. In the present example, the word "ANT" might be represented by a pattern of activation that includes some of the same nodes as those in the pattern that represents "RUN." Similarly, we might imagine further modifications of the model in which the letter nodes are replaced by letter patterns, the feature nodes are replaced by feature patterns, and perhaps even the extreme case in which all the representations--for features, letters, and words--are patterns of activation defined over all the nodes in the model.
Figure 2: The interactive-activation model of reading modified to include distributed representations for words.
Although it has become common to speak of local and distributed models as well as representations, most connectionist models contain both local and distributed representations, in various proportions. For purposes of understanding Fodor and Pylyshyn’s argument, however, it is useful to begin with an extreme case, that of "ultralocal" models. An ultralocal connectionist model is one in which there are only local representations. The original interactive model of reading (shown in Figure 1) approximates this case. The most relevant thing to notice about such models is that they do not contain any syntactically complex symbols. Since local symbols (individual nodes) do not have symbols as parts, they are syntactically simple. If ultralocal models provide a general account of the mind, therefore, the language-of-thought hypothesis is false. Fodor and Pylyshyn argue, however, that ultralocal connectionist models do not provide a general account of the mind. This is because these models fail to explain certain pervasive facts about human cognition, most importantly what Fodor and Pylyshyn call "systematicity." Although they try to extend these arguments to connectionist models other than ultralocal ones, it is best to begin with the ultralocal case.
The mark of systematicity, for Fodor and Pylyshyn, is the presence of presupposition relations among mental capacities. For example, our ability to have certain thoughts presupposes an ability to have certain others. For some reason, we never find people who can entertain the thought that Mary loves John without being able to entertain the thought that John loves Mary. Nor do we find people who can form an idea of a cup of black coffee without being able to form an idea of a black cup of coffee. And so on, for most familiar mental states. Inferential capacities are also systematically related; we don’t find people who can infer P&Q from P&Q&R, for example, but who can’t infer P from P&Q.<12> Fodor and Pylyshyn argue that pervasive presupposition relations can hardly be accidental, and so a theory of cognition should provide a guarantee of systematicity.
On the assumption that mental symbols have syntactic parts, we can explain how the mind implements systematic relations among attitudes. A possibility at one extreme is that two systematically related token attitudes physically overlap, i.e., share some of the same token parts.<13> Alternatively, such attitudes might contain tokens of a physical kind such that they can easily be reproduced from or matched against one another. This would allow the implementation of inferential processes such as variable-introduction and variable-binding, which are sensitive to the syntactic structure of symbols, and are thereby sensitive to some of the semantic dependencies of the attitudes the symbols help to realize.<14>
On the other hand, according to Fodor and Pylyshyn, ultralocal models contain no mechanism for insuring that any given node presupposes the existence of any other node. There is thus no explanation of the systematic relations between, say, the thought that Mary loves John and the thought that John loves Mary. If these thoughts were realized as individual connectionist nodes, Fodor and Pylyshyn argue, there would be no principled reason that one thought is thinkable by all and only the people able to think the other. Someone who wished to embrace ultralocal connectionist models as plausible alternatives to languages of thought might, perhaps, be willing to settle for a huge number of stipulations about the mental "hardware"--e.g., an ad hoc stipulation to the effect that the two nodes that realize these particular thoughts about John and Mary do in fact presuppose one another. But this would seriously weaken the case against the LOT hypothesis. Until some connectionist mechanism is specified that can insure that the stipulations hold, it is reasonable for Fodor and Pylyshyn to point out that the only known mechanism for doing so is one that includes syntactically structured symbols. If their criticisms are correct, then while ultralocal models may be appropriate for certain aspects of cognition (such as initial processing in reading), these models may have to share space in the mind with LOT models. Therefore, ultralocal connectionist models would not provide critics of the language-of-thought hypothesis with a plausible, general alternative.
It appears that many of the most prominent connectionist commentators are willing to concede this result to Fodor and Pylyshyn, with a reminder that ultralocal models are atypical of connectionist models in general. Before looking at the wider class of connectionist models, however, I want to consider two lines of reply that, if correct, would rescue even ultralocal models from Fodor and Pylyshyn’s criticisms.
Many philosophers hold that systematicity is a conceptual necessity rather than a fact in need of psychological explanation. They hold that it is simply part of proper practices of thought-ascription that if one can’t think that John loves Mary, then one can’t think that Mary loves John (see Evans, 1983). How might this view, if correct, be used on behalf of ultralocal models? It might be argued that ultralocal models can guarantee systematicity of thoughts, because if a node in a particular model fails to stand in a systematic presupposition relation to another one, we should simply refuse to ascribe to it the content that Mary loves John or that P&Q. Far from being a mystery for ultralocal connectionists, systematicity is a conceptually necessary feature of cognition. Thought must be systematic, because whatever isn’t, isn’t thought.
Fodor concedes that his argument "takes it for granted that systematicity is at least sometimes a contingent feature of thought," for otherwise "you don’t need LOT to explain the systematicity of thoughts" (Fodor, 1987a, p. 152). I think this is understating his case, however. Even if the philosophical position described in the previous paragraph is correct, and correct for every case of systematicity, a variant of Fodor and Pylyshyn’s argument still applies. For if it is a requirement on the ascription of thoughts that they be systematically related, then ultralocal connectionist models simply have no explanation of how we do manage to have the thought that Mary loves John or that P&Q. This becomes clear if we introduce the term "pseudothoughts" for entities that are exactly like thoughts, except that they fail to enter into the requisite systematic relations. A pseudothought that Mary loves John, then, is something that would be a thought that Mary loves John, if only the pseudothinker were capable of thinking that John loves Mary, etc. Given this notion, the basic premise of Fodor and Pylyshyn’s argument can be rephrased as follows: while we regularly find people who think a wide variety of thoughts, we never find people who merely pseudothink. It is surely not an accident that every person has many genuine thoughts, but it is a mystery why this should be so if thoughts are realized as individual nodes. In other words, by enforcing a strict conceptual requirement on thought ascription, we are left with no account of how people manage to have as many thoughts as they do--assuming that these thoughts are realized by ultralocal models.<15> To provide such an account, ultralocal models need to provide some mechanism for insuring that systematic relations hold among nodes, and this is precisely what Fodor and Pylyshyn argue has not been accomplished.
In the previous paragraph I mentioned that we have "many" (systematically related) thoughts. This fact is relevant to a different argument against Fodor and Pylyshyn, one which appeals to the possibility of evolutionary rather than cognitive explanations of systematicity. Consider a creature with only a few systematically related thoughts--say, an insect-like creature capable of "thinking" only that warm food is near, that cold water is near, that cold food is near, and that warm water is near. Would such a creature be a mystery for an ultralocal connectionist theory (say, one that holds that these four insect-thoughts are realized by nodes n1,...,n4, respectively)? Yes, in the sense that the connectionist architecture itself does not explain why every insect has all four nodes. However, the connectionist could appeal to an alternative explanation of this fact, perhaps a biological or evolutionary one. It may simply be that nodes n1,...,n4 represent what they do innately. Thus, some critics of Fodor and Pylyshyn have concluded that evolutionary theory can rescue connectionism from the systematicity argument (Braddon-Mitchell and Fitzpatrick, 1990; Sterelny, 1990). However, human systematicity and bug systematicity are relevantly different. Humans have vast numbers of thoughts, which, moreover, vary from person to person. We need an explanation of the systematic relations among the capacities to have these thoughts. On the assumption that not all of these capacities are wholly innate, a directly biological or evolutionary explanation of the copresence of human thoughts is implausible. Of course, an indirect explanation might well be acceptable--in particular, one that holds that evolution explains systematicity via explaining the presence of a cognitive architecture that explains systematicity. But then, Fodor and Pylyshyn’s argument is that the only cognitive architectures available to play this mediating role are LOT architectures.
2 Distributed Connectionism and the LOT Hypothesis
Connectionist opponents of the language-of-thought hypothesis have considered their most powerful weapon to be features of distributed symbols, or contentful patterns of activation of multiple nodes. If Fodor and Pylyshyn’s argument were directed solely at ultralocal models, therefore, it would be little cause for connectionist alarm. My first task will be to discuss their attempt to extend their conclusion from ultralocal to distributed cases (section 2.1). My claim will be that they fail to show that distributed connectionist models that account for systematicity are likely to implement a language of thought. This will pave the way for a consideration of the two major attempts to provide actual counterexamples to their conclusion, in the form of distributed models that account for systematicity without syntactic structure: Paul Smolensky’s "coffee case," (section 2.2) and Tim van Gelder’s account of "nonconcatenative compositionality" as exemplified in representational schemes such as Smolensky’s "tensor product" framework (section 2.3). I will argue that, on a careful analysis of these models, they do in fact use syntactically structured representations. If this is right, Fodor and Pylyshyn’s main claim--that connectionism will not falsify the LOT hypothesis--withstands the fall of their argument. In the final section, I will substitute a positive argument for this claim.
2.1 The limitations of Fodor and Pylyshyn’s argument
Surprisingly, Fodor and Pylyshyn say next to nothing by way of extending their conclusions about the ultralocal case to their conclusions about connectionism in general. While they consider the path between the two conclusions to be short, it is not immediately clear from their discussion what they consider the path to be. This has led critics to misidentify Fodor and Pylyshyn’s strategy for extending their conclusions, or even to suggest that they offer no extending argument at all.<16> What they do say is confined to a single sentence in a footnote, a comment on the particularly crude ultralocal network shown in Figure 3, which they use in mounting their systematicity argument. (The labels "A," "B," and "A&B" are not parts of the model; rather, they specify the contents of the nodes.) Before proceeding, let me recap their argument that such ultralocal models cannot account for systematicity. The key problem they identify for ultralocal models is that there is no plausible connectionist mechanism for insuring the presence of one node given another. Given connectionist architecture, it is perfectly possible for a mental life to contain node 1 in the diagram without containing node 2 or node 3. For that reason, as I have put it, ultralocal connectionists must implicitly make large numbers of independent, ad hoc, assumptions about presupposition relations among bits of mental hardware (i.e., among the individual nodes that realize systematically related symbols).
Figure 3: Fodor and Pylyshyn’s (1988) sample ultralocalist network for drawing inferences from A&B to A or to B.

Given this way of looking at the argument about ultralocal models, we can understand their attempt to extend the argument to distributed models:
To simplify the exposition, we assume a ‘localist’ approach, in which each semantically interpreted [symbol] corresponds to a single Connectionist [node]; but nothing relevant to this discussion is changed if these [symbols] actually consist of patterns over a cluster of [nodes]. (Fodor and Pylyshyn, 1988, p. 15)<17>
Given the astonishing brevity of this formulation, it is perhaps understandable that critics have either ignored it or responded to it with an equally brief assertion that there is "no argument to be found there" (Chalmers, 1990, p. 4). Nevertheless, the passage contains an argument of some force. Fodor and Pylyshyn’s idea is to have us imagine an interpretation of Figure 3 on which the circles signify groups of nodes rather than individual nodes. The point of this seems clear. Just as there is no plausible mechanism for insuring the presence of a particular individual node given another individual node, so there is no mechanism for insuring the presence of a particular group of nodes given another group. The only way to insure systematicity, for such models, is simply to posit for each bit of hardware (i.e., each relevant group of nodes) that there are certain corresponding bits of hardware (i.e., other relevant groups of nodes).
The fundamental difficulty with Fodor and Pylyshyn’s attempt to extend their argument to distributed symbols is that it assumes that the distributed symbols are realized by distinct groups of nodes. It appears likely, as they insist, that given the presence of one group of nodes, there is nothing to insure the presence of another, distinct, group of nodes. However, on many of the most interesting connectionist schemes of representation, distributed symbols are patterns of nodes that overlap. How might this help to account for systematicity? Suppose that s1 and s2 are systematically related symbols, realized in a particular distributed connectionist model as different patterns of activation levels p1 and p2 over the same group of nodes n. Given that the model can produce s1, it must contain the nodes over which s2 is distributed--namely, n--since the two symbols are distributed over the very same nodes. To explain why the two symbols are systematically related, then, one doesn’t need to make ad hoc assumptions of presuppositions among various bits of hardware. All that is needed is some mechanism for insuring that a model capable of producing pattern p1 over a group of nodes is also capable of producing some other pattern p2 over the same nodes. This is fundamentally a programming problem for connectionism; the hardware problem is nonexistent. Fodor and Pylyshyn have given no reason to suppose that this programming problem cannot be solved in a general and principled fashion. They have simply failed to address the most formidable connectionist models, those based on overlapping distributed symbols.
Of course, this purely negative point does not mean that distributed models can be developed that insure systematicity without appealing to syntactically structured representations. Perhaps the only way to insure systematic relations among overlapping patterns of activation is to identify subpatterns as syntactic parts. Or perhaps not.<18> At this stage, only examination of particular representational schemes will help to decide this point. That is what I want to do in the rest of this paper. I will consider models that illustrate two broad strategies connectionist opponents of the LOT hypothesis might pursue. Since there are two requirements on syntactic complexity--a symbolic-parthood requirement and a semantic-dependence requirement (see section 1.1)--a connectionist model needs only to fail one or the other of these requirements in order to avoid a language of thought. One option for a connectionist is to account for systematicity with distributed models in which symbols do have symbolic parts, but do not stand in an appropriate semantic dependence relation to these parts. The best-articulated example of such a strategy is Paul Smolensky’s influential coffee example, which I discuss next.<19> A second strategy is to seek to account for systematicity with distributed models in which symbols stand in appropriately semantic dependence relations, without standing in part/whole relations. I will consider Tim van Gelder’s attempt to analyze Smolensky’s "tensor product" networks in this way, and then conclude with more general reasons why no connectionist counterexamples to Fodor and Pylyshyn’s claims are likely to be forthcoming.
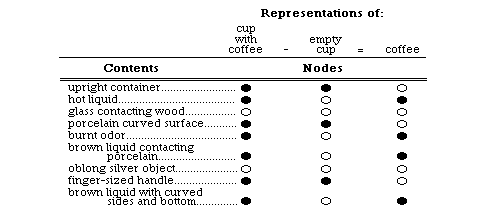
Smolensky is concerned to highlight various differences between complex LOT symbols and corresponding distributed connectionist symbols. He draws a contrast between a particular LOT symbol of a cup with coffee--the formula "with(cup,coffee)"--and a particular distributed connectionist representation of a cup with coffee. In the typical LOT case, it is possible to start with the complex symbol, and "subtract" the representation of an empty cup--say, "with(cup,NULL)"--to produce a representation of coffee itself. Furthermore, this representation of coffee is context-independent in that it retains its meaning in other complex symbols, such as "with(can,coffee)," "with(tree,coffee)," and "with(man,coffee)." Smolensky suggests that we perform a corresponding subtraction procedure on a distributed connectionist representation of cup with coffee, to see if what results can properly be called "a connectionist representation of coffee." His arrangement can be pictured as in Figure 4. (The black dots in the rightmost three columns represent, respectively, the nodes constituting Smolensky’s representations of cup with coffee, empty cup, and coffee. The left column represents the content of each individual node.)
Figure 4: Smolensky’s (1989) connectionist representation of coffee.
Smolensky emphasizes two features of this representational scheme.
First, unlike local symbols (see section 1.2), the representation of cup with coffee has a sort of "compositional structure," since it can be formed by combining the other two groups of nodes. The model therefore provides at least a measure of systematicity among the symbols for cup with coffee, empty cup, and coffee. Second, Smolensky hesitates to call this compositional structure syntactic structure, since he insists that the structure is present only in an "approximate" sense. What he means by this is that, unlike in the LOT case, the coffee symbol (represented by the black nodes in the rightmost column) is not a context-independent representation of coffee. Instead, Smolensky suggests, it is "really a representation of coffee in the particular context of being inside a cup." We can see why he says this by looking at the contents of the darkened nodes: hot liquid, burnt odor, contacting porcelain, etc. Also, as he points out, if we were to start with corresponding assemblies of nodes representing can with coffee, tree with coffee, or man with coffee, subtraction would result in very different representations of coffee: as burnt smelling granules stacked in a cylindrical shape (from the subtracted can), as brown beans hanging in mid-air (from the subtracted tree), or as a cup with coffee (from the subtracted man). Therefore, he concludes:
[The structure is] not equivalent to taking a context-independent representation of coffee and a context-independent representation of cup --and certainly not equivalent to taking a context-independent representation of in or with--and sticking them all together in a symbolic structure, concatenating them together to form the kind of syntactic compositional structures like "with(cup,coffee)" that [Fodor and Pylyshyn] want connectionist nets to implement. (Smolensky, 1989, p. 11)
In short, according to Smolensky, the context dependence of the representations in the model keep it from implementing a language of thought.
To assess this argument, one thing we need to know is what the relevance of context dependence is for the fate of the language-of-thought hypothesis. Here we must be particularly careful to respect the distinction between languages of thought in general and particular preconceived implementations of languages of thought. The two questions I distinguished in section 1.1 must be kept separate in dealing with Smolensky’s distributed coffee model:
(1) Does the model implement a language of thought?
(2) Does it implement some (or any) particular preconceived implementation of a language of thought?
It is easy to imagine that context dependence is relevant to question (2). Many traditional LOT models do not employ context-dependent symbols, so that Smolensky can use context dependence to distinguish his coffee model from those. To say that context dependence is relevant to question (2) is not to say that it is conclusively relevant, since there might be some traditional models that do exhibit context dependence.
However this issue is settled, something more is needed to show that context dependence is even partially relevant to question (1), the question that Fodor and Pylyshyn address. In particular, it must be shown that context independence is required for syntactic structure. If it is not required, then Smolensky’s argument is simply misdirected. He does not take a clear stand on this point, saying for example that context dependence renders the structure of representations "approximate." Certainly he provides no argument to the effect that syntactic structure requires context independence. Given this, it appears likely that this is due to a confusion of questions (1) and (2). Setting this aside, however, we need to consider what can be said in defense of the idea that context independence is a requirement on syntactic complexity.
As I mentioned in section 1.1, there is widespread agreement (for better or worse) that syntactically complex symbols not only have symbolic parts, but also depend semantically on these parts, in the sense that the meaning of a syntactically complex symbol must depend on the meanings of its parts. Now suppose that a particular symbol a (connectionist or not) is context dependent, having different meanings as part of the symbols Fa, Ga, etc. Then it seems wrong to suppose that the meaning of Fa depends on the meaning of a. Instead, the dependence relation is reversed: the meaning of a seems to depend on the meaning of Fa. At best, the meaning of Fa depends on some property of a other than its meaning. We might imagine, for example, that there is some property of a other than its meaning, which is context independent and which, together with context, determines its context-dependent meaning. The meaning of the resulting symbols Fa, Ga, etc. would depend on this property of a, but this would not be a dependence relation between meanings, and so would not be a semantic dependence relation of the sort typically required. Consequently, context independence is at least an initially plausible requirement on syntactic complexity.<20> Whether it is a genuine requirement on syntactic complexity depends, among other things, on whether semantic dependence, or indeed any semantic relation, is genuinely required of syntactic complexity. But for purposes of this paper I am working along with the consensus that these requirements are genuine.
Even if a defender of the language-of-thought hypothesis must favor (at least some degree of) context independence, it is possible to take a more direct tack in replying to Smolensky. I would like to make a case for denying that his coffee case does display context dependence. The illusion of context dependence stems from misassignments of content. Consider again the darkened nodes in the first column of the previous diagram. Smolensky says that when these nodes are activated, they form a symbol with the content cup with coffee (or the proposition that a cup with coffee is around, or some such content). An alternative interpretation is that the assembly of nodes has as its content the conjunction of the contents of the individual nodes. If when one node is on, it means upright container, and when another is on, it means hot liquid, why shouldn’t the two together mean upright container and hot liquid? Following this train of thought, we might conclude that the assembly in the third column is not a context-dependent representation of coffee, but a straightforward, context-independent representation of hot brown liquid with burnt odor, curved sides, and bottom contacting porcelain. Why isn’t Smolensky’s third column simply a syntactic concatenation of a symbol for hot liquid, one for burnt odor, and so on? This looks exactly like an implementation of the following "syntactic compositional structure that [Fodor and Pylyshyn] want connectionist nets to implement":
HotLiquid(x) &
BurntOdor(x) &
BrownLiquidContactingPorcelain(x) &
BrownLiquidWithCurvedSidesAndBottom(x)
There are several advantages to this interpretation. First, it is more precise, and reflects better the system’s treatment of the symbols. For example, imagine what would show that the content of the first column was cup with coffee instead of this alternative. Plausibly, a deciding factor is whether the symbol (even ideally) responds to cups with samples of coffee other than hot, brown liquids with . . ., such as cups with dried coffee, or cups with coffee beans, etc. But this is precisely what Smolensky’s alleged cup with coffee symbol does not (even ideally) do, by his own hypothesis.<21>
It is worth describing one other manifestation of the fact that Smolensky’s content ascription is too generous. After illustrating the variety of coffee symbols in different contexts (cup, can, tree, man, etc.), he makes the following provocative claim:
That means that if you want to talk about the connectionist representation of coffee in this distributed scheme, you have to talk about a family of distributed activity patterns. What knits together all these particular representations of coffee is nothing other than a type of family resemblance. (Smolensky, 1989, p. 12)
On my suggested reinterpretation, we can see that the alleged role of family resemblance is also an illusion. Suppose we interpret the system as having a variety of symbols representing hot brown liquids . . ., burnt smelling granules . . ., hanging brown beans . . ., and so on. Even having every member of this "family" of symbols is not enough to represent something as coffee. To do this, plausibly, a system must at least represent the hot liquid in the porcelain as the same kind of stuff as the granules in the cylinder or the beans on the tree. Furthermore, it is important to realize that this is not at all explained by Smolensky’s "family resemblance" of the assemblies of nodes. For all Smolensky says, there is no (causally) relevant respect in which these nodes resemble each other any more than they do any other random assemblies! Instead, for all Smolensky has shown, what is needed is for the system to contain another symbol that it can use to categorize all of these assemblies as being about the same stuff. And why wouldn’t that symbol be a context-independent representation of coffee?<22>
I conclude that Smolensky’s coffee case constitutes no threat at all to the language-of-thought hypothesis. The appearance of a threat stems from Smolensky’s mistaken assignments of particular contents to his models.<23> As far as I can tell, my reinterpretation strategy does not depend on the particular contents Smolensky assigns to the individual nodes in the coffee model (e.g., hot liquid, burnt odor, etc.). Although Smolensky suggests that the "microfeatures" represented by individual nodes in more realistic models will be less easily expressed in natural language, my argument will generalize to these cases. The reinterpretation strategy seems to depend only on Smolensky’s assertion that symbols for coffee are composed of symbols for microfeatures of coffee.<24> Can Smolensky run a version of his argument without microfeatures? I don’t think so. Without microfeatures, although Smolensky could stipulate that coffee is represented by a number of distinct groups of nodes on different occasions, he would have no argument for context sensitivity—that is, no argument that these different groups of nodes have (even slightly) different contents (e.g., coffee in the context of a cup, coffee in the context of a tree, etc.).
2.3 Nonconcatenative complexity
Recently, Tim van Gelder has tried a different strategy in response to Fodor and Pylyshyn. His argument seems best described with the aid of a generic example. Suppose that s and w are mental symbols--connectionist or not--and that s means sugar and w means white. Suppose that we are interested in developing a representational framework involving such symbols, one that exhibits systematicity. This would involve, at a minimum, the framework’s supporting the use of s, w and other symbols to generate systematically related symbols such as a symbol P with the content that there is a cup with coffee and white sugar, and a symbol Q with the content that there is a white cup with coffee and sugar. As van Gelder points out, such a framework should provide "general, effective and reliable processes" for producing P and Q given s, w, and other symbols, and for using P or Q inversely to produce these symbols (van Gelder, 1990, p. 5). Call these processes "conversion processes." His argument rests upon a distinction between two ways of providing conversion processes.
The first is the familiar method of forming syntactically complex symbols, by "concatenating" s, w, and other symbolic parts to form systematically related wholes such as P and Q. Since, on this method, s and w are physically present within P and Q, it is fairly easy to design processes that can "parse" P or Q back into their parts; in effect, P and Q "wear their logical form on their faces." van Gelder is clear that models employing this first method are implementations of the language-of-thought hypothesis, whether they are connectionist or nonconnectionist. However, he introduces a second sort of conversion method in which the systematically related symbols are "nonconcatenative." He cites several examples of connectionist models (ones with distributed symbols) that have the interesting feature of providing the required conversion processes without preserving s, w, et al. as literal parts of P and Q. He emphasizes that in a nonconcatenative scheme of representation the systematically related symbols such as P and Q do not literally contain symbols corresponding to semantic constituents, such as s and w. Therefore, these systematically related symbols have no syntactic structure. It is this feature that van Gelder exploits to argue that connectionist models using nonconcatenative conversion processes can explain systematicity without satisfying the language-of-thought hypothesis.
I think it should be conceded without a fuss that nonconcatenated symbols don’t satisfy the LOT hypothesis, since they don’t have symbolic parts. Rather, a defense of the LOT hypothesis should begin with a reminder of the obvious: the hypothesis doesn’t say that every mental symbol is syntactically complex, but says only that some are (or, as I suggested in section 1.1, that enough are to generate the expressive power of the portion of natural language that one comprehends). Furthermore, of course, from the fact that van Gelder’s models<25> use some syntactically simple symbols, it doesn’t follow that they use no syntactically complex ones. Indeed, my strategy will be to argue that these models do, and apparently must, supplement the use of nonconcatenative symbols with straightforwardly concatenative ones. If so, this is enough to show that they implement languages of thought.
To begin, I want to look at a conversion method that, while nonconcatenative in van Gelder’s sense, is clearly part of a language-of-thought model. Suppose that people have syntactically complex mental symbols--for illustration’s sake, we can suppose that these are tiny strings that resemble English formulae, such as "there is a cup with coffee and white sugar," and that homunculi use tiny blackboards for writing and erasing these formulae. Also, suppose that in many cases the homunculi are unable to store the formulae efficiently in memory--perhaps the boards fill up. To alleviate the problem, we might imagine, the homunculi take to storing synonymous, but syntactically simple, substitutes for these formulae. For lack of a better word, call these substitutes "abbreviations." Which abbreviations they choose don’t concern us, so long as they can reliably convert between the syntactically complex formulae and the abbreviations.<26> Of course, there is a price for using these abbreviations to save board space: to perform inferences, the homunculi must first convert an abbreviation back into its expanded, syntactically complex, form. Nevertheless, it is easy to imagine the space savings to be worth the extra effort during inference.
The point of describing this fanciful model is that, although its method of conversion is nonconcatenative, it does support syntactically complex symbols (used in inference), and so is a genuine language-of-thought model. My suggestion is that, at least as far as the fate of the LOT hypothesis is concerned, the connectionist models van Gelder discusses do not differ from this model. There are no blackboards and no homunculi in these models, and the tiny English symbols are replaced with distributed symbols--groups of nodes--but the relevant features are the same. The most important shared feature is that, in inference, the nonconcatenated abbreviations in the connectionist models must first be converted into syntactically complex form.
To see this, suppose that a group of nodes P is a nonconcatenative but systematically generated abbreviation, with the content that there is a cup with coffee and white sugar. What is needed in order for a system to use this stored "belief" in inference, say, to draw conclusions about how to prepare breakfast this morning? Since P is nonconcatenative, it is in effect a "blob" whose internal structure may differ radically from that of a symbol with a semantically "near" content--say, that there is a can with coffee and white sugar--and may be nearly identical structurally to a symbol with a "distant" content—say, Sonny drinks more coffee than Cher. At a minimum, then, the system would need to be able to regenerate, from P, symbols for cup (as opposed to some other container, such as a can or a supermarket) and with coffee and sugar (as opposed to some other fact about the cup). Once these symbols are regenerated, of course, they must not be allowed simply to "drift apart," effectively losing the information that the coffee and sugar are in the cup, but must be used jointly in planning breakfast. But to use them in this manner is no different from using them as systematic, symbolic parts of a syntactically complex whole, a concatenative symbol with the content that there is a cup with coffee and sugar. This complex symbol is the "mereological sum" of the two symbols plus whatever items indicate that their roles are tied to one another. It is syntactically complex because its content is appropriately dependent on that of its symbolic parts (the symbols for cup and with coffee and sugar).<27> While it is true that van Gelder’s models present ways of reducing the number of syntactically complex symbols that must be present at any one time, this is also true of the fanciful language-of-thought case. The relevant similarities between the connectionist models and the model with homunculi and blackboards are deep enough, I think, to compel the conclusion that all are alike in making crucial use of a language of thought for inference, if not for long-term storage in memory.
It is possible to modify van Gelder’s nonconcatenative models so that they avoid commitment to syntactically complex symbols. Specifically, the models can be redesigned to perform inferences without the regeneration (or decomposition) steps. Such "shortcut" inferences are easy to implement in connectionist networks: all that is needed is to build connections between the nonconcatenative symbols themselves, so that P (say) might activate some other abbreviation Q without the system needing first to decompose P or Q.
To see the effects of this, consider again the analogy with the homunculi and blackboards. In the original story, given the ability to decompose the abbreviations in inference, the homunculi can engage in "structure-sensitive" processing. What this means, at a minimum, is that the homunculi can apply fairly general rules--such as, "if I want some X and there is some in container Y, then find container Y"--to a variety of specific representations--such as the belief that there is sugared coffee in the cup, or the belief that there are tools in the hardware store. This is possible because, with syntactic complexity, the homunculi can "match" the rules to the representations in virtue of the form of their parts, binding variables to constants, and the like (see the illustration of production systems in section 1.3). If we suppose that the homunculi forego decomposition of the abbreviations into complex counterparts, however, this sort of inference would be precluded.
Instead of being capable of structure-sensitive inference with general rules, the system would need an immense independently stored battery of information about every specific case it represents (e.g., tea and spark plugs as well as coffee, and bags and warehouses as well as cups). Either all of this information would have to be innate, or else the system would have to find out "the hard way" that it should find a cup when some desired sugared coffee is in the cup, and even then it would have no way of applying such information to analogous problems such as what to do when some desired tea is in a bag. As a result, at very best, the system would only perform sensibly in routine situations: everyday, highly practiced activities performed under optimally smooth conditions<28>.
This limited, structure-insensitive sort of inference is known as purely "associative" or "statistical" inference (Hume’s "habits of the mind"). As most connectionists agree, it is characteristic of connectionists models that use only local symbols (individual nodes), such as the interactive activation model of reading (see section 1.2). A desire to avoid pure associationism is a major reason for the popularity of models with distributed symbols, and in particular for the models that van Gelder discusses. To redesign these models, then, would deprive them of their most attractive feature, namely, their ability efficiently to combine structure-sensitive and associative inference. Indeed, if structure-sensitive inference is abandoned, these models lose their advantage over models involving only local symbols. Without inferential processes that are sensitive to the form of nonconcatenative abbreviations, and without processes for converting these abbreviations back into syntactically complex formulae, there is little computational point to using distributed rather than local symbols for the abbreviations (in fact, the increased complication carries with it some computational disadvantages such as decreased speed). Cheapened versions of van Gelder’s models--ones stripped of their support for syntactic complexity--would have as little hope to be the whole story of cognition as do models with only local symbols. But this is simply to reiterate the dilemma for connectionists posed by Fodor and Pylyshyn--connectionists appear forced to choose either to implement a language of thought or else to adopt pure associationism. The point of my argument has been to show that this dilemma remains standing even though Fodor and Pylyshyn’s argument falters, and even in the face of the most sophisticated connectionist schemes of representation yet offered.
2.4 A more general perspective
Connectionists have not shown that distributed models can account for systematicity without implementing a language of thought. It may appear that my arguments about Smolensky’s and van Gelder’s models are general enough to be recast into a general argument that no connectionist model can explain systematicity without syntactic complexity. If so, there may be a suspicion that my formulation of the LOT hypothesis is too weak to be of explanatory interest. In other words, it is natural to ask whether and how it is possible for any model to abandon the LOT hypothesis without sacrificing systematicity.
To see how this is possible, consider the following example of a "drinks machine," adapted from Martin Davies (1989).<29> The outputs of the machine are drinks of one of four kinds: coffee or tea with or without milk. The inputs of the machine are tokens ("coins") of four kinds: A, B, C, D. The relations between the inputs and outputs are as follows:
A-token in ® coffee with milk out
B-token in ® coffee without milk out
C-token in ® tea with milk out
D-token in ® tea without milk out
Imagine that the tokens, when put in the machine, realize "thoughts" about the drinks they respectively cause the machine to produce (e.g., the thought that the customer wants coffee with milk). Given this, we can apply Fodor and Pylyshyn’s notion of systematicity, and ask whether there are presupposition relations among these representations.
Suppose that the machine is so constructed that, given that it can think that the customer wants coffee with milk and that the customer wants tea without milk, it must be able to think that the customer wants coffee without milk and that the customer wants tea with milk. (Translation: given that the machine can process A-tokens and D-tokens, it must be able to process B-tokens and C-tokens.) If (as we are supposing) these presupposition relations are not accidental, then (as Davies argues) the machine must contain four mechanisms M1,...,M4 of the following sort:
M1 explains coffee delivery given A-tokens or B-tokens;
M2 explains tea delivery given C-tokens or D-tokens;
M3 explains milk delivery given A-tokens or C-tokens;
M4 explains milk nondelivery given B-tokens or D-tokens.
But if this is the case (as Davies also argues) these pairs of tokens must share distinctive properties to which their respective mechanisms are sensitive. For example, M1 might respond to roundness, M2 to squareness, M3 to redness, and M4 to blueness. In this case A-tokens would have to be round and red (since they trigger both M1 and M3), B-tokens would have to be round and blue, C-tokens square and red, and D-tokens square and blue. Davies argues that the insertion of tokens (i.e., the thoughts) would therefore qualify as syntactically complex states, articulated into shape-related states (representing demand for coffee or tea) and color-related states (representing demand for milk or no milk).
Along these lines, Davies shows how it is possible to argue a priori (or, at least, "prior" to psychological research) for the presence of syntactic complexity, given systematicity. If this is right, then it is no surprise that the various distributed connectionist models I have discussed all turn out, on close inspection, to implement a language of thought. However, since the LOT hypothesis is intended to be a substantive psychological explanation of systematicity, there is reason to resist a construal of the LOT hypothesis that renders it logically (or at least physically) equivalent to the existence of systematicity. The account of syntactic structure I have been working with is stronger than Davies’ account in one crucial respect, and can therefore be used to show how it is at least possible to account for systematicity without syntactic structure.
On the account of syntactic structure I have adopted, (proper) syntactic parts must be (proper) spatiotemporal parts, as (written or spoken) words are spatiotemporal parts of sentences. (In a moment I will illustrate the explanatory importance of this requirement.) By this criterion, an object’s state of being round is not a syntactic part of its state of being round and red, since their spatiotemporal locations coincide.<30> It is possible for representational states (in addition to representational objects) to have spatiotemporal syntactic parts. The state of activation of a connectionist node n at time t is, for example, a spatial part of the state of activity of n and another node n’ at t, and is a temporal part of the state of activation of n at t and t’. This is why the nodes in Smolensky’s coffee model (see section 2.2) combine to form syntactically complex symbols, for example.
Syntactic complexity appears inevitable if each systematically-related symbol is a combination of states or objects with different spatiotemporal locations. To explain systematicity without a language of thought, then, a representational scheme might be developed in which each systematically-related symbol is a combination of states with the same locations. For short, let us say that such models support only "nonspatiotemporal combination." In Davies’ drinks-machine example, this is achieved by treating a systematically-related symbol as a combination of simultaneous states of the same object. I will conclude by considering an analogous strategy for mental symbols: models in which symbols combine only by being simultaneous states of the same object.
Although this strategy may seem easy to implement, in fact it raises serious computational difficulties (which in turn help to explain the appeal of genuine languages of thought, with spatiotemporal combination). Natural languages and genuine languages of thought (including the connectionist models I have considered in the previous two sections) can have an indefinitely large "primitive vocabulary" consisting of simple symbols (e.g., nodes, patterns of nodes, or strings of letters or sounds). The number of primitive vocabulary elements in English appears to be at least as large as the number of entries in a standard dictionary, and the number of elements in an English speaker’s (hypothetical) language of thought appears to be at least as large as the number of English primitive vocabulary elements the person understands. These symbols can enter into fairly large combinations with other symbols by being placed in certain spatiotemporal relations (to which processes are sensitive). For example, easily comprehensible English sentences can run to twenty or more primitive elements (e.g., words), as can sentences in a (hypothetical) language of thought.<31> Furthermore, these combinations are "nonexclusive" in the sense that virtually any pair of primitive elements can enter into some sensible combination or other--as virtually any two words (or ideas) can be combined in some sentence (or thought). It is not at all clear how fairly large, nonexclusive combinations formed from indefinitely large vocabularies can be implemented in a system that supports only nonspatiotemporal combinations.
In such models, states must "combine" by being simultaneous states of the same object (on pain of not being in the same place and time, and so of being spatiotemporally concatenated). If two such states are mutually inconsistent--e.g., an object’s being round and it’s being square--then they cannot be combined in this way. If combinations are to be nonexclusive, the primitive vocabulary of such a system must be realized as a stock of mutually consistent states. Furthermore, like all mental symbols, these states must be causally relevant to the behavior of the system. The problem is: how can there be enough such states to go around?
Consider, first, the situation with respect to individual connectionist nodes. Such a node typically has only two mutually consistent, causally relevant states at a given moment: its activation level and its threshold (or degree of activation necessary for it to transmit activation to other nodes).<32> If a model’s primitive vocabulary elements are realized as particular momentary activation levels or thresholds, and if they are to combine nonspatiotemporally, then at most they can combine two at a time--in mentalistic terms, the most complex thoughts would involve only two ideas. Although a node may change activation level and threshold over an extended time interval, this does not help the situation. A combination of activation levels (or thresholds) of an object, as they exist at different moments, is a syntactic complex of these states, since it has them as temporal parts.<33> Therefore, local representation can support large, nonexclusive, combinations of primitive vocabulary elements only by supporting (temporal) syntactic complexity.
The analysis of distributed representations is more complicated, as usual. It may appear that groups of nodes are in more causally relevant states at a time, and so may support large combinations of primitive vocabulary elements without supporting syntactic complexity. In particular, it appears that a group of k nodes has 2k causally relevant states at a given time, corresponding to the activation and threshold states of each node in the group at that time. For example, consider two nodes n1 and n2, each with a state of activation and a threshold state. Now consider their mereological sum, the pair of nodes. Call this object "Fred." At any time, Fred is in four relevant states: its n1-activation, its n1-threshold, its n2-activation, and its n2-threshold. If states are located where their participating objects are located, as I have been supposing, then all of these states are in the same place--namely, where Fred is--and so their combinations do not count as syntactically complex. If we consider larger n-tuples of nodes, it might be suggested, we can accommodate large combinations of primitive vocabulary elements without postulating a language of thought.
However, I think we should reject the idea that all states are located precisely where their participating objects are. The central--perhaps, only--explanatory function of the notion of a state’s spatial location is to track and explain which other states it can influence in a given time.<34> The states that now exist wholly within my room, for example, cannot influence the states existing next month wholly within a room a light-year away. In many cases we lose this sort of explanation, if we adhere to the principle that states are where their participating objects are. For example, suppose that n1 and n2 are at such a distance from one another that light travels from one to the other in a positive (but perhaps very tiny) time interval e. Then (by special relativity) it is not physically possible for Fred’s n1-activation at t to influence Fred’s n2-activation at any time before t+e. If we suppose that these states are located in the same place, however, we lose a straightforward explanation of this fact. If, instead, we suppose that Fred’s n1-activation is where n1 is, and Fred’s n2-activation is where n2 is, then we can explain their inability to influence each other in suitably small times. But given any account of state-location that tracks influential potential in this fashion, combinations of Fred’s four states would count as syntactically complex--as containing the states as spatial parts. Therefore, connectionist representational schemes restricted to combinations of simultaneous states of an object are unable to support large combinations of primitive vocabulary elements, even if the objects in question are distributed.
Although we can explain systematicity without a language of thought (e.g., by tokens of the drinks-machine sort), the price (in any known connectionist mechanism, at least) seems to be a primitive vocabulary that lends itself only to combinations of extremely small size. In fact, the problem is even more severe. In a genuine language (or language of thought) a symbol can contain multiple "copies" of the same type of primitive vocabulary element (e.g., "John loves Mary more than Sally loves Harry"). There does not seem to be an analogous possibility in connectionist systems restricted to nonspatiotemporal combinations: it doesn’t make sense for an object to have multiple "copies" of the same state type (that is, at the same time--copies at different times would qualify as temporal and so syntactic parts of the whole). Without a language of thought, combinations must not only be small, but must also be restricted in combinatorial possibilities (e.g., recursion).
If (as seems likely, although I know of no way to prove it) models with symbols analogous to Davies’ drinks-machine tokens are the only possible nonsyntactic explanations of systematicity, we would have a fairly general reason to deny that connectionist models are likely to explain systematicity without implementing a language of thought. Importantly, this would be achieved without making it literally impossible to explain systematicity without a language of thought. The argument for the LOT framework (and so for models that fall under both the connectionist and LOT frameworks) rests on its ability to account for a family of intuitively obvious but fully empirical phenomena, including but not restricted to systematicity, large primitive vocabularies, large nonexclusive combinations of primitive vocabulary elements, and (even limited) recursion.
If we look beyond connectionism, there are possibilities for nonspatioteporal combinations of states that do not seem to suffer from the expressive limitations I have mentioned. Wayne Davis has suggested to me (in conversation) that a "wave model" of cognition can explain how mental states can combine in large quantities, while occupying the same spatiotemporal regions. Suppose we want to explain the systematic relations between the capacities to think that John loves Mary and that Mary loves John. If we think of the mind as analogous to an audio speaker, we might suppose that John is represented by the sound of an oboe, Mary by the sound of a trumpet, loving by the sound of a drum, etc. (Furthermore, John’s role as agent might be represented by the fact that the oboe is playing middle "C", multiple "occurrences" of John might be represented by multiple oboes, etc.) This would provide the resources for explaining systematicity, but since all of these sound waves occupy the same locations, they do not combine syntactically to constitute a language of thought. There is, of course, room to worry about the details of such a scheme--for instance, since waves interfere with one another, would the model be able to cope with the resulting "cacophony"? However, the important question for present purposes is whether or not connectionist opponents of the LOT hypothesis can find solace in the wave model.
For reasons I have mentioned, representations realized in connectionist activation patterns must combine spatiotemporally, and so appear to work like "particles" rather than waves. It is sometimes said, however, that representations realized in the weights of a network’s connections are superimposed like waves (and are subject to a rather severe kind of cacophony). The wave model might be helpful to connectionists, then, if all of the representations in a connectionist model were "in the weights". A relevant disanalogy between the wave model and connectionist models appears, however, when we distinguish between "standing" and "transient" representations. Transient representations are representations of inputs and outputs, as well as representations that exist only during the "inferential" transitions from inputs to outputs. Standing representations exist at other times, and are typically the basic "inference rules" (or "rules of thumb", perhaps) by which inputs lead to outputs. A sound-wave model can treat both standing and transient representations as waves. On the contrary, connectionist models seem forced to locate at least transient representations in activation patterns rather than weights, since weights simply do not display the required kind of transience and variability from input to input. In effect, then, at least transient connectionist representations must work like particles rather than waves. Nevertheless, the wave model serves as a useful reminder that, even if we assume representationalism, the LOT hypothesis is a substantive empirical hypothesis, one which would be rendered false if it turned out that propositional attitudes were wholly realized in overlapping "brain waves".
NOTES
<1>Representationalism, at least given this weak interpretation, is not the focus of the dispute between Fodor and Pylyshyn and their connectionist critics. This fact allows us to make do with a cursory explanation of the key terms that figure in the statement of representationalism. Mental "symbols" are the (hypothetical) physical embodiments of ideas, where an idea is something that can figure in many different attitudes to the same (or conceptually related) propositions. "Computation," to a first approximation, is a process of using representations as premises or conclusions of inferential processes. See Lormand, 1990b, for a detailed account of these notions.
<2>To avoid repeated use of the modifier "syntactic," I will often speak of "complexity" and "simplicity" intending the modifier to be understood.
<3>We can come to understand the current debate without considering whether the following account is ultimately the right account of syntactic complexity. This is because no critics of Fodor and Pylyshyn--at least none of which I am aware--have taken issue with this account. While the dispute has been operating at an intuitive level, however, perhaps some of the consequences of this account will motivate devoting more attention to the notion of syntactic complexity itself.
<4>Although there may be viable but weaker conceptions of syntactic complexity according to which syntactic constituents do not need to be parts of complex symbols, Fodor is emphatic that parthood is required for a language of thought. He insists repeatedly that the LOT hypothesis claims that "(some) mental formulas have mental formulas as parts" (Fodor, 1987a, p. 137), and that this notion of parthood is literal:
Real constituency does have to do with parts and wholes; the symbol ‘Mary’ is literally a part of the symbol ‘John loves Mary’. It is because their symbols enter into real-constituency relations that natural languages have both atomic symbols and complex ones. (Fodor and Pylyshyn, 1988, p. 22)
While Fodor appears to endorse a weaker account of complexity in a recent paper (Fodor and McLaughlin, 1990), we will see in the final section that without the requirement of spatiotemporal parts, the LOT hypothesis becomes nearly trivial.
<5>If (some) mental symbols are physical occurrences (e.g., states or events) rather than ordinary physical objects, then the LOT hypothesis demands a notion of spatiotemporal parthood for (token) occurrences as well as for (token) individuals. There is some leeway in the construction of such a notion. This issue will loom large in the final section of this paper, in the course of my positive argument that connectionists are not likely to avoid commitment to languages of thought.
<6>See Lormand, 1990b, for an account of semantic dependence that is consistent with arguments against the analytic/synthetic distinction.
<7>A weaker construal of the LOT hypothesis is required for nonlinguistic thinkers, such as monkeys and babies, and for nonlinguistic faculties of the adult mind. However, I don’t know how to specify, without bare stipulation, how much syntactic complexity should be required in these cases, if any.
<8>There is no requirement to the effect that simple symbols in natural language must correspond to simple symbols in a language of thought. On many traditional LOT models, individual words in natural language are analyzed into conglomerations of mental "feature" symbols that, taken individually, are unexpressed in natural languages. This is why Smolensky’s distinction between "conceptual-level" and "subconceptual-level" semantics is irrelevant to the language-of-thought hypothesis (Smolensky, 1988).
<9>For readers unfamiliar with these architectures, the details will not be relevant. For the sake of concreteness, one can think of any high-level programming language--such as Basic, Pascal, or Fortran--when I mention production systems or logic-based systems. Each of these programming languages supports syntactically complex symbols, yet they all differ in the primitive symbol manipulations they make possible. This suits them well as analogies for cognitive architectures in the language-of-thought mold.
<10>I have found that some people find it unnatural to speak of "implementations" of representational schemes, such as a language of thought. They often prefer to speak of "realizations" or "instantiations" of representational schemes, and "implementations" of algorithms. This does not appear to be of more than terminological significance. If "implementation" is only possible for algorithms, it is trivial to reformulate the claim (which I attribute to Fodor and Pylyshyn, and will defend) that connectionism must implement syntactically complex symbols. The claim is that connectionism must implement some algorithm or other that operates on syntactically complex representations. The substance of the arguments in this paper are unaffected by this reformulation.
<11> I attempt to counter some of his criticisms in Lormand, 1990a.
<12>These examples all consist of pairwise presupposition relations between attitudes. Systematicity applies more generally as a relation between groups of attitudes: e.g., the availability of the pair of thoughts that sugar is white and that coffee is brown presupposes the availability of the pair of thoughts that coffee is white and that sugar is brown. This is so even though these thoughts do not enter into pairwise presupposition relations to one another.
<13>This is the case with certain semantic (or propositional) networks of the sort often contained in traditional cognitive-scientific models (for a review, see Johnson-Laird, et al., 1984). In such a network, nodes are symbols for objects and properties (among other things), and pieces of the network (i.e., groups of nodes along with their connections) are symbols that help to realize attitudes. Groups of attitudes (thought to be) about the same thing (e.g., toothpaste) typically share a node representing that thing. This allows mechanisms easily to implement inferential relations among these attitudes.
<14>This sort of matching occurs, for example, in "production system" models (see Anderson, 1983; Holland, et al., 1986). In these models, a thinker’s thoughts and goals are realized by storing syntactically complex symbols in various buffers, including long-term and working memory, where they may be acted upon by inferential processes. Some of these inferential processes are realized by special kinds of "IF...THEN..." rule-symbols called "productions." Although details vary from theory to theory, a production may be thought of as a rule-symbol with a (tiny) processor. The processor’s task is to watch out for the presence of a symbol matching its "IF" part (modulo differences between variables and constants), and to perform some simple action corresponding to its "THEN" part, such as forming a copy of the "THEN" part in working memory (perhaps with variables bound or introduced). It is as if one could write a conditional sentence in a book, give it tiny eyes and arms, and give it one reflex: when you see a copy of your "IF" part written somewhere, write down a (possibly modified) copy of your "THEN" part (or do something comparably simple). With the use of variables, a single production (e.g., "IF x is white, THEN x is not yellow") can implement systematic inferential relations among a wide range of pairs of token attitudes that have parts of a single physical type (e.g., the beliefs that toothpaste is white and that toothpaste is not yellow, the desires that teeth are white and that teeth are not yellow, etc.).
<15>A possible escape route for the defender of connectionist models is to appeal to a behaviorist or instrumentalist theory of mental states that denies representationalism (see Clark, 1989, for such a response to Fodor and Pylyshyn). Consideration of such a view is beyond the scope of this paper, which seeks to operate within the mainstream cognitive-scientific (and mainstream connectionist) assumption of representationalism.
<16>For example, while Fodor and Pylyshyn argue persuasively and at some length that distributed models don’t necessarily yield systematicity, Smolensky mistakenly takes this to be an argument to the effect that distributed representation cannot yield systematicity (Smolensky, 1989, p. 8). For a similar suggestion see Chalmers, 1990, p. 4.
<17>Fodor and Pylyshyn use the term ‘units’ for what I have been calling ‘nodes’, and the word ‘nodes’ for what I have been calling ‘symbols’. I have altered their quotation accordingly.
<18>For certain purposes, Fodor and Pylyshyn’s failure to consider overlapping distributed representations is a good thing. They want to show that no connectionist models can insure systematicity without implementing syntactically complex symbols. They do not and should not want to make the stronger claim that no connectionist models can implement complex symbols, period. This stronger claim appears to be false, since connectionist networks can implement Turing machines (at least those with a finite tape), and Turing machines can implement complex symbols. But it is at first difficult to see how Fodor and Pylyshyn’s argument can avoid this strong conclusion. Since they argue that ultralocal models do not implement syntactic complexity, and assert that "nothing is changed" by moving to distributed models, their argument seems to apply to all possible connectionist models. Chalmers (1989) offers a "refutation" of their argument based on this fact. His objection fails because what Fodor and Pylyshyn are actually claiming is that "nothing is changed" by moving to distributed models by substituting distinct groups of nodes for distinct individual nodes. This leaves open the possibility that some connectionist models may implement syntactic complexity. However, it also leaves open the possibility that these models may implement systematicity without complexity, so Fodor and Pylyshyn fail to accomplish their argumentative goal.
<19>While I concur with most of the criticisms of Smolensky provided by Fodor and Mclaughlin (1990), my criticisms will be independent and, I hope, supplementary.
<20>A more careful account would distinguish between two sorts of context dependence: (1) context dependence of contents, in which a single symbol changes meanings depending on what other symbols are present, and (2) context dependence of symbols, in which a single content is expressed by different symbols depending on what other symbols are present. While the first case is that treated in the text, it appears that Smolensky’s model is at best an example of the latter variety: he suggests that coffee is represented by different sets of nodes in different contexts. The conditions for syntactic complexity are violated in some, but not all, such cases. Let a1, a2, etc. be all the potential coffee symbols in a given model. Let C(a1), C(a2), etc. be the set of contexts in which a1, a2, etc., respectively, are used to mean coffee. If each ai, taken alone, means coffee, then despite the multiplicity of coffee symbols, the semantic condition for syntactic complexity is met: the content of each member of C(ai) depends on the content of ai. The exceptional case is that in which some ai--say, a1--fails to mean coffee when taken alone. In this case, the content of a1 changes depending on its context, and so we have the same situation as that discussed in the text. For all Smolensky indicates, however, his various coffee symbols do represent coffee when taken alone. (What else might they represent? Tea? Nothing at all?) I don’t know whether this is an artifact of his particular example.
<21>Similarly, it is not clear that the symbol (even ideally) avoids responding to cups with fake coffee--hot, brown liquids with . . ., but which are not coffee.
<22>One way for this to happen is for this symbol to be a shared (token or type) part of the various assemblies Smolensky speaks of as bearing a family resemblance to one another. It may even be the symbol’s sole function to label the assemblies as representing the same kind of stuff, and so to label information about one as relevant to hypotheses about the other. If Smolensky wishes to avoid postulating a separate coffee symbol that is used to "knit together" the various coffee-assemblies, and if he wishes to deny that there are any microfeatural representations common to all these assemblies, then he needs some other explanation of how the system treats the various assemblies as representations of the same kind of stuff.
Perhaps Smolensky’s idea of "family resemblance" is to be cashed out as follows: the hot brown liquid . . . assembly shares some critical number of nodes with the burnt smelling granules . . . assembly, which in turn shares the critical number of different nodes with the hanging brown beans . . . assembly, and so on. If this is so, although the hot brown liquid . . . and hanging brown beans . . . assemblies (say) would not share the critical number of nodes needed to be classified immediately as representing the same kind of stuff, the system might classify them as doing so, by virtue of detecting a chain of sufficiently overlapping assemblies that "connects" them. If the same-stuffness of hot brown liquid . . . and hanging brown beans . . . (and all the other relevant entities) is kept implicit in the existence of these chains, then the system can avoid having a coffee symbol. In order to determine whether two assemblies represent the same kind of stuff, the system might attempt to find a suitable chain between the two assemblies. I don’t know whether such a search process can be constrained to the right sort of chains (e.g., to exclude representations of tea, cocoa beans, etc.), and Smolensky provides no hints as to whether this is even the sort of account he would wish to develop.
<23>I have been speaking as if the existence of more precise assignments of content shows that Smolensky’s assignments of content are, strictly speaking, wrong. On a more "relaxed" account of content, however, it might be that Smolensky’s less precise assignments are as legitimate as those I suggest. Unfortunately for Smolensky, a more relaxed theory of content would defeat his argument from the very start. If we were willing to be loose with content assignments, the English phrases "hot brown liquid . . ." and "hanging brown beans . . ." would themselves qualify as context-dependent representations of coffee. The same would be true for analogous phrases in a language of thought. Given this result, there would be no room for Smolensky to insist that languages of thought lack context-dependent representation, and no room for Smolensky to insist on a difference between his coffee model and fully-fledged languages of thought.
<24>Strictly speaking, the strategy also depends on the conjoinability of the microfeatural symbols. But all this requires is that the microfeatures be microproperties or microrelations--conjoinable as "F(x1,...,xn) & G(y1,...,ym)"--or else microoccurrences--conjoinable as "p & q"--or else microobjects--conjoinable as "a & b." There is no indication from connectionist theories that microfeatures might be anything else.
<25>van Gelder’s role in this discussion is that of a philosophical commentator, so that the phrase "van Gelder’s models" should be taken as shorthand for "the models that van Gelder considers," a broad class including, most notably, Smolensky’s tensor-product representations (Smolensky, 1989).
<26>As van Gelder illustrates, they might adopt a Godel-numbering scheme for the formulae, substituting numbers for formulae in a way that is known to allow for "general, effective, and reliable" conversion processes. On this scheme, rather than storing a cumbersome syntactically complex symbol such as "there is a cup with coffee and white sugar," the homunculi would store some numeral (perhaps in compact, scientific notation, with base 1000). Except by the rare accident, this numeral would not contain any parts corresponding to the parts of the original string--i.e., it would not contain numeric abbreviations for "cup," "white," and so on. This would not, then, count as a concatenative conversion process.
<27>These points are clearer when we realize that, in the general case, it would not be enough to regenerate only the symbols for cup and with coffee and sugar. All regenerating these symbols tells the system is that P says something or other about cups and sugared-coffee containers. This is compatible with P’s meaning that Cher once spilt a cup with coffee and sugar on Sonny, or something equally irrelevant to the search for this morning’s coffee. When more and more symbols must be regenerated, and more and more items are needed to maintain information about their roles with respect to one another, it is increasingly evident that what is regenerated from the stored nonconcatenative symbols are genuinely syntactic formulae. In the next (and final) section I support this analysis by considering the possibility that the regenerated symbols might not combine spatiotemporally, unlike genuine syntactic parts.
<28>Notice that van Gelder’s models would not avoid the LOT hypothesis simply by adding direct connections between nonconcatenative symbols, while leaving intact the mechanism for decomposing these symbols to handle nonroutine situations. Rather, the decomposition mechanism must be completely disabled for purposes of inferential processing. Chalmers (1990) appears to miss this point.
<29>As will become clear, the morals I wish to draw from the drinks machine differ from, and apparently contradict, the morals Davies wishes to draw.
<30>This holds on the natural assumption that a state is where the individuals that "participate" in the state are. (Where did Mary hug John? Wherever Mary and John were, of course.) While this assumption is natural, it must be amended, as I will explain shortly.
<31>There is a tradeoff between primitive vocabulary size and required combination size. The number of primitive mental elements available to a person might be smaller than the number of primitive linguistic elements he understands, if the person supposes that the linguistic elements are definitionally reducible to a small stock of mental elements. In this case, however, these mental elements would have to be capable of entering into larger combinations than the linguistic elements, to form symbols with the same content.
<32>Although some connectionist models exploit a few more states, such as a node’s "resting" activation level, nothing essential to my argument will turn on ignoring these nuances.
<33>Although I have considered only the case in which the vocabulary elements are activation states (and thresholds) of a node at a moment, nothing is changed by generalizing to the case in which the vocabulary elements are patterns of activation states (or patterns of thresholds) of a node over an interval. Since a node can have only one activation level (and one threshold) at a given moment, it can have only one pattern of activation levels (and one pattern of thresholds) over a given interval. If such patterns are to combine nonsyntactically, they also can combine at most two per interval. Finally, a combination of patterns of activation levels (or thresholds) of an object, as they exist over different (possibly overlapping) intervals, is a syntactic complex of these states, since it has them as temporal parts.
<34>Other functions of the notion of a state-location, such as helping to specify where one has to be to witness the state at a certain time, depend on this function.
REFERENCES
Anderson, J., 1983: The Architecture of Cognition, Harvard University Press, Cambridge.
Block, N., ed., 1980: Readings in Philosophy of Psychology, Harvard University Press, Cambridge.
Braddon-Mitchell, D. and J. Fitzpatrick, 1990: "Explanation and the Language of Thought", in Synthese.
Chalmers, D., 1990: "Why Fodor and Pylyshyn Were Wrong: The Simplest Refutation," manuscript.
Clark, A., 1989: Microcognition, MIT Press, Cambridge.
Davies, M., 1989: "Concepts, Connectionism, and the Language of Thought," Proceedings of the International Colloquium on Cognitive Science.
Evans, G., 1983: The Varieties of Reference, Oxford University Press, Oxford.
Fodor, J., 1975: The Language of Thought, Harvard University Press, Cambridge.
Fodor, J., 1981: Representations, MIT Press, Cambridge.
Fodor, J., 1987a: "Why There Still Has to be a Language of Thought," in Psychosemantics, MIT Press, Cambridge.
Fodor, J. and B. McLaughlin, 1990: "Connectionism and the Problem of Systematicity: Why Smolensky’s Solution Doesn’t Work", in Cognition.
Fodor, J. and Z. Pylyshyn, 1988: "Connectionism and Cognitive Architecture," in Cognition.
Holland, J., K. Holyoak, R. Nisbett, and P. Thagard, 1986: Induction, MIT Press, Cambridge.
Johnson-Laird, P., D. Herrmann, and R. Chaffin, 1984: "Only connections: A critique of semantic networks," Psychological Bulletin.
Lormand, E., 1990a: "Framing the Frame Problem," in Synthese. [See update: "The Holorobophobe's Dilemma"]
Lormand, E., 1990b: "Classical and Connectionist Models of Cognition," Ph.D. Thesis, MIT.
Rumelhart D., and J. McClelland, 1982: "An interactive activation model of context effects in letter perception," in Psychology Review.
Rumelhart D., G. Hinton, and J. McClelland, 1986: "A General Framework for Parallel Distributed Processing," in J. McClelland and D. Rumelhart, ed., Parallel Distributed Processing, v. 1, MIT Press, Cambridge.
Smolensky, P. 1988: "On the Proper Treatment of Connectionism," in The Behavioral and Brain Sciences.
Smolensky, P. 1989: "Connectionism, Constituency, and the Language of Thought," manuscript.
Sterelny, K. 1990: The Representationalist Theory of Mind, Blackwell.
van Gelder, T. 1990: "Compositionality: A Connectionist Variation on a Classical Theme," in Cognitive Science.