Skip to: site menu | section menu | main content
Krzysztof J. Fidkowski
My research interests include development of robust solution techniques for computational fluid dynamics, error estimation, computational geometry management, parallel computation, large-scale model reduction, and design under uncertainty. Some current and recent research projects are:
Machine learning anisotropy detection
Hybridized and embedded discontinuous Galerkin methods
Output-based error estimation and mesh adaptation
Adaptive RANS calculations with the discontinuous Galerkin method
Unsteady output-based adaptation
Entropy-adjoint approach to mesh refinement
Contaminant source inversion
Cut-cell meshing
Nonlinear model reduction for inverse problems
Back to top
Machine learning anisotropy detection
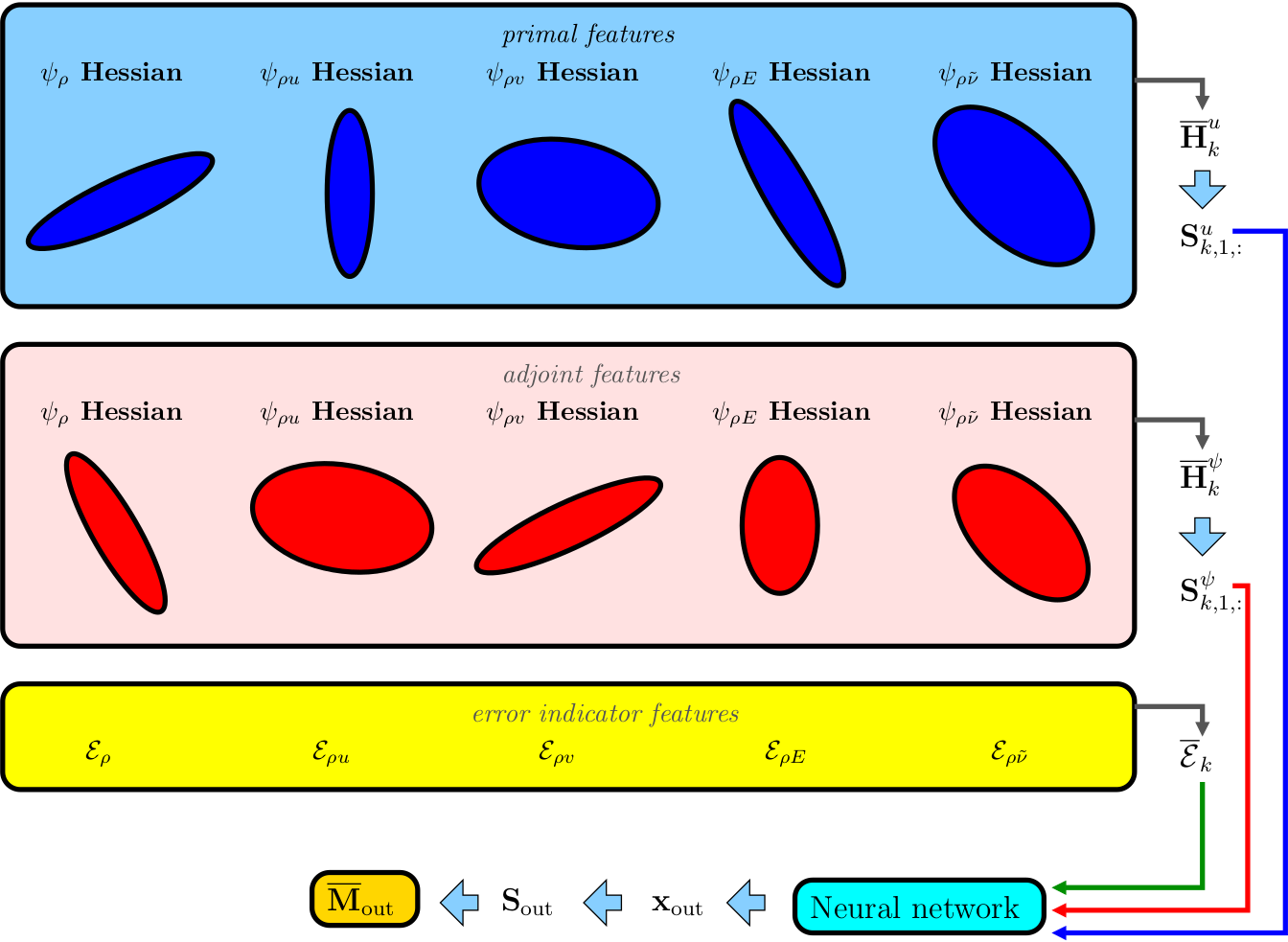
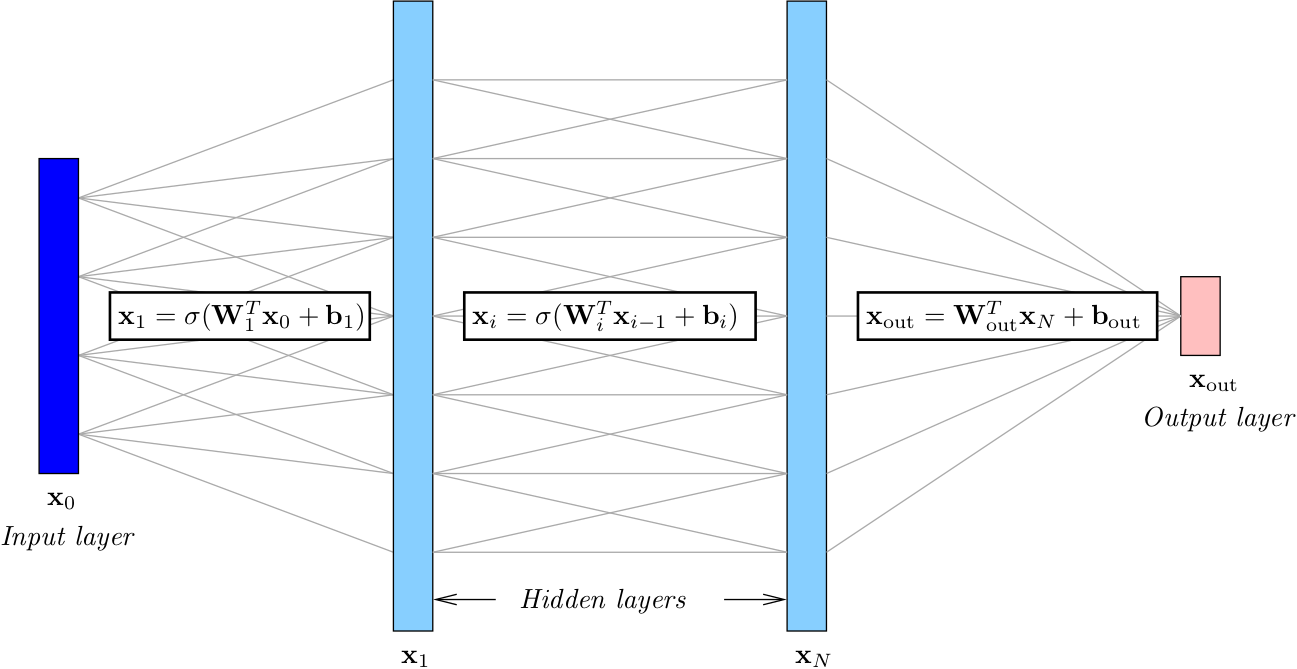
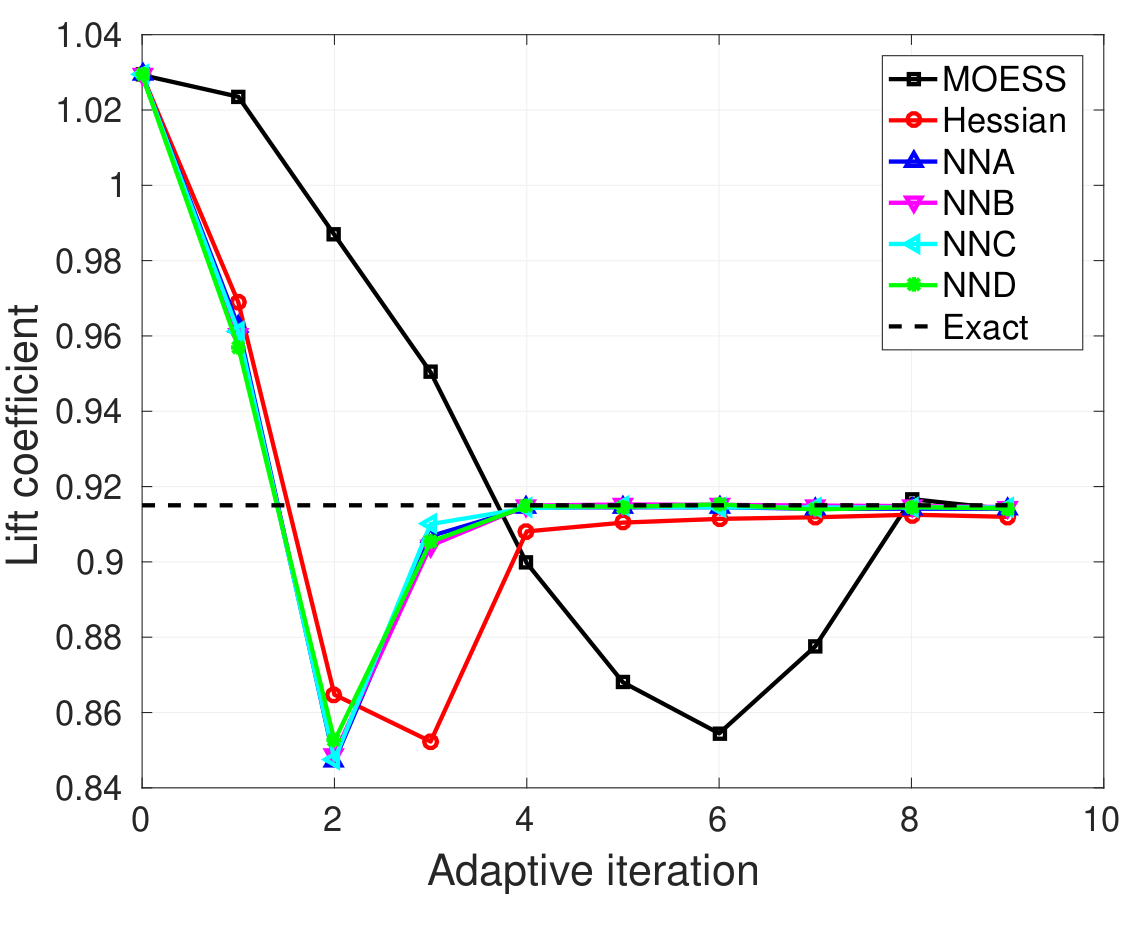
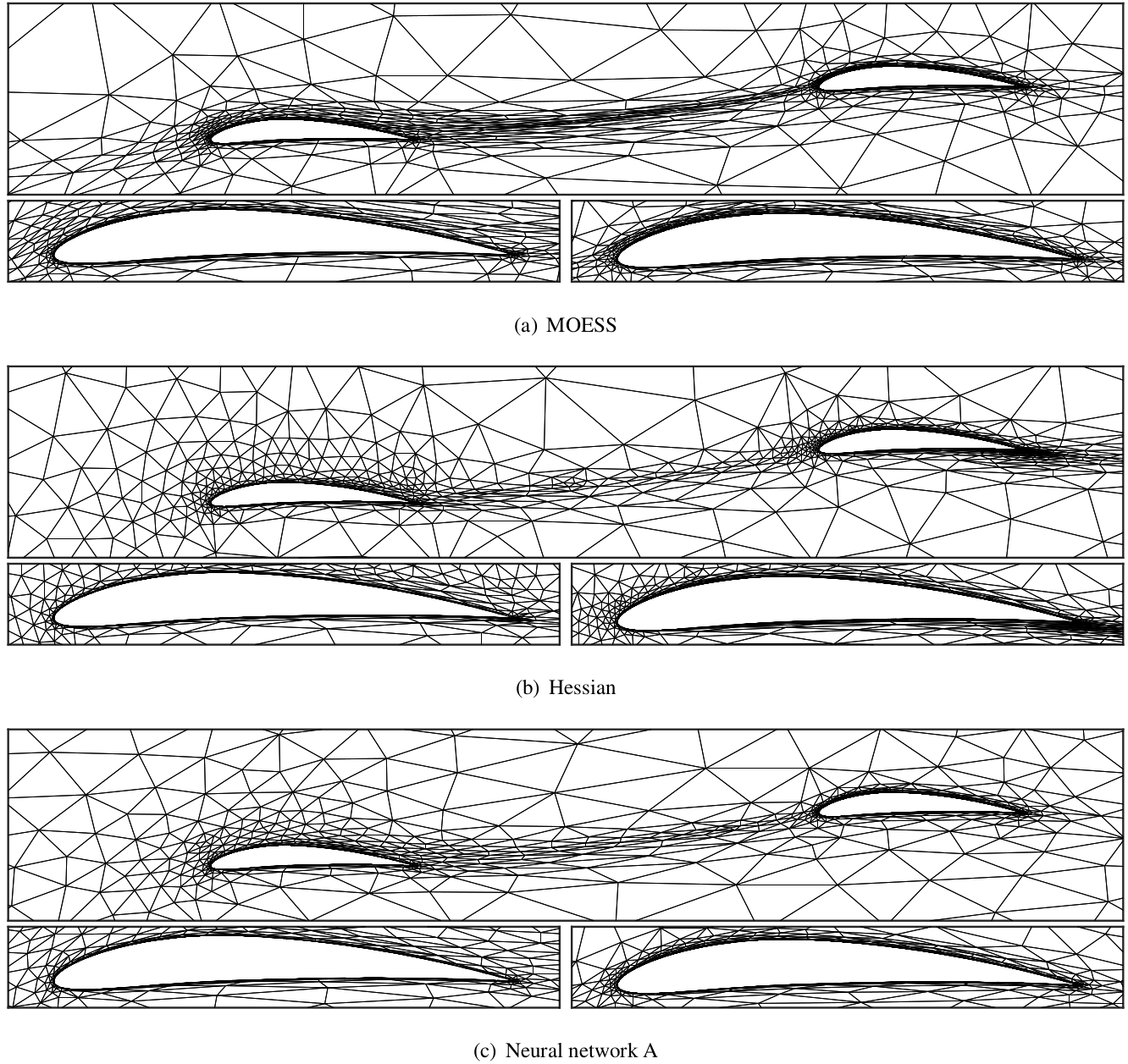
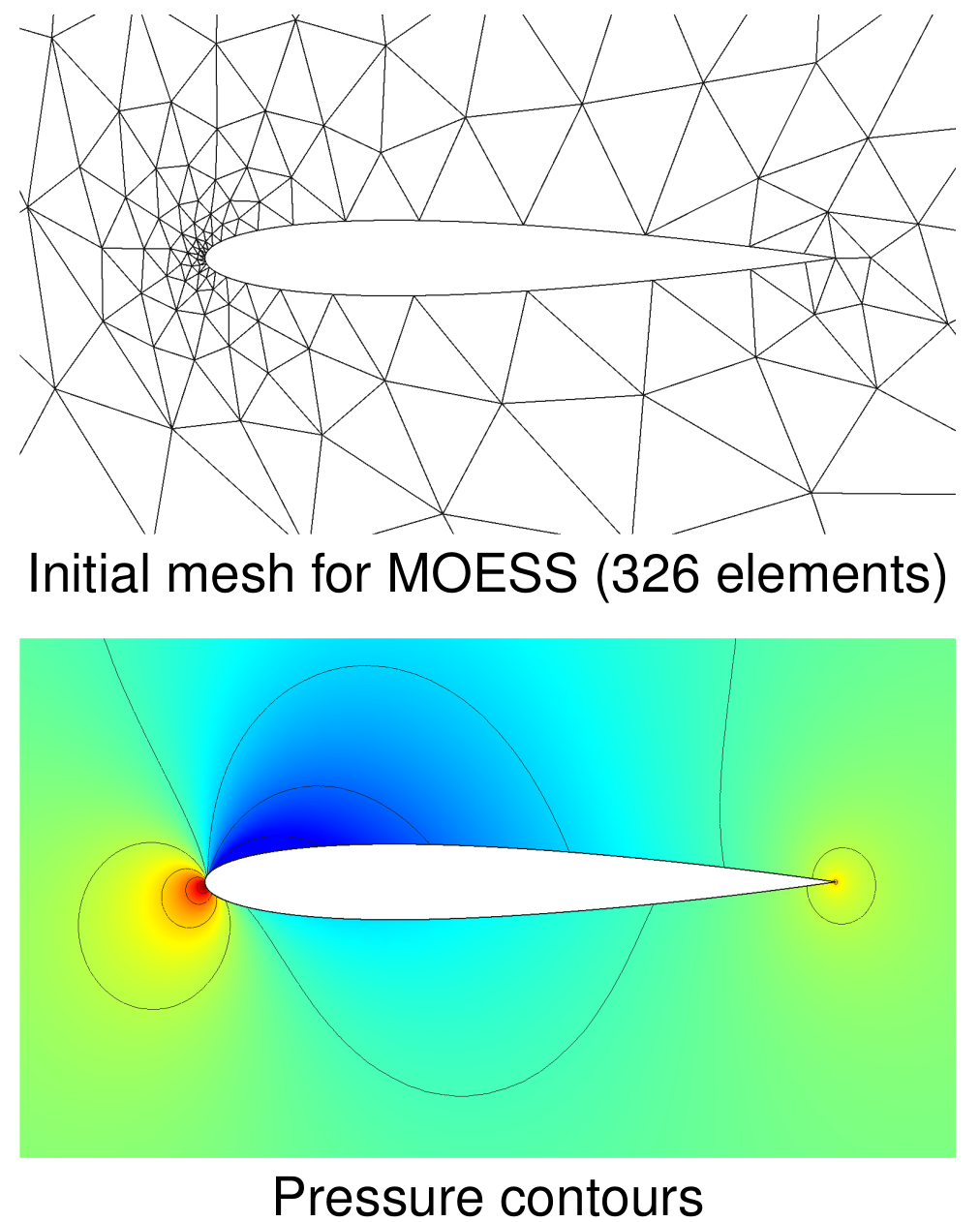
Numerical simulations require quality computational meshes, but the construction of an optimal mesh, one that maximizes accuracy for a given cost, is not trivial. In this work, we tackle and simplify one aspect of adaptive mesh generation, determination of anisotropy, which refers to direction-dependent sizing of the elements in the mesh. Anisotropic meshes are important for efficiently resolving certain flow features, such as boundary layers, wakes, and shocks, that appear in computational fluid dynamics. To predict the optimal mesh anisotropy, we use machine learning techniques, which have the potential to accurately and efficiently model responses of highly-nonlinear problems over a wide range of parameters. We train a neural network on a large amount of data from a rigorous, but expensive, mesh optimization procedure (MOESS), and then attempt to reproduce this mapping from simpler solution features. Ongoing research directions in this are include:- Extension to three dimensions
- Testing on a wider variety of fluid flows
- Prediction of sizing as well as anisotropy
 Relevant Publications
Relevant Publications
Krzysztof J. Fidkowski and Guodong Chen. A machine-learning anisotropy detection algorithm for output-adapted meshes. AIAA Paper 2020--0341, 2020. [ bib | .pdf ]
Back to topHybridized and embedded discontinuous Galerkin methods
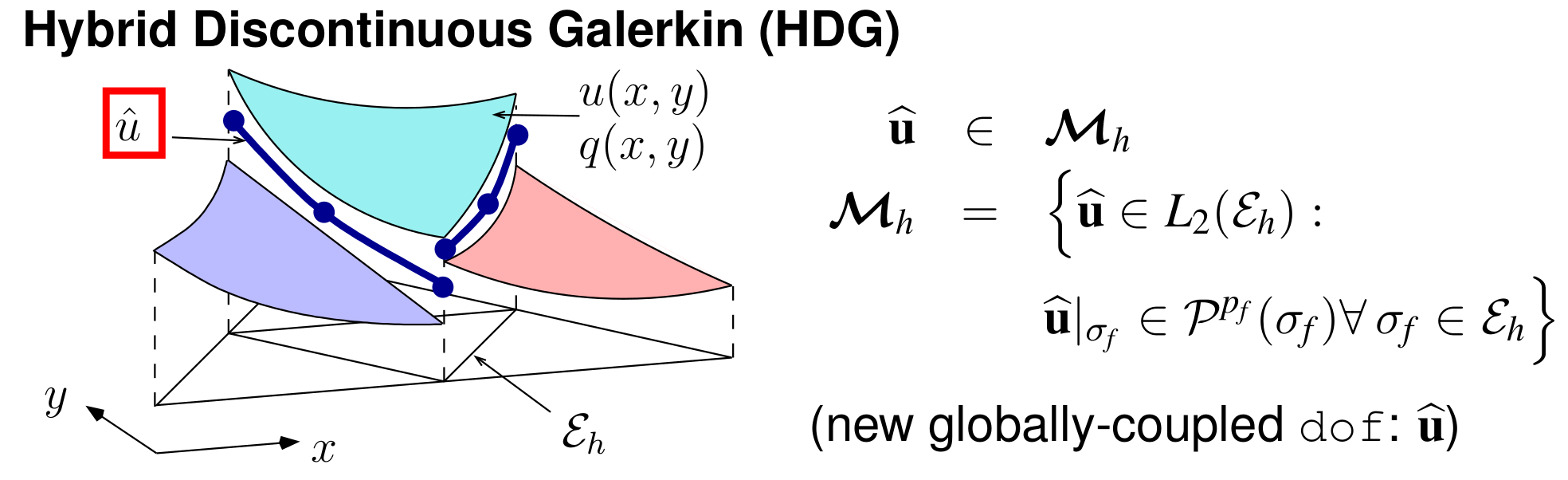
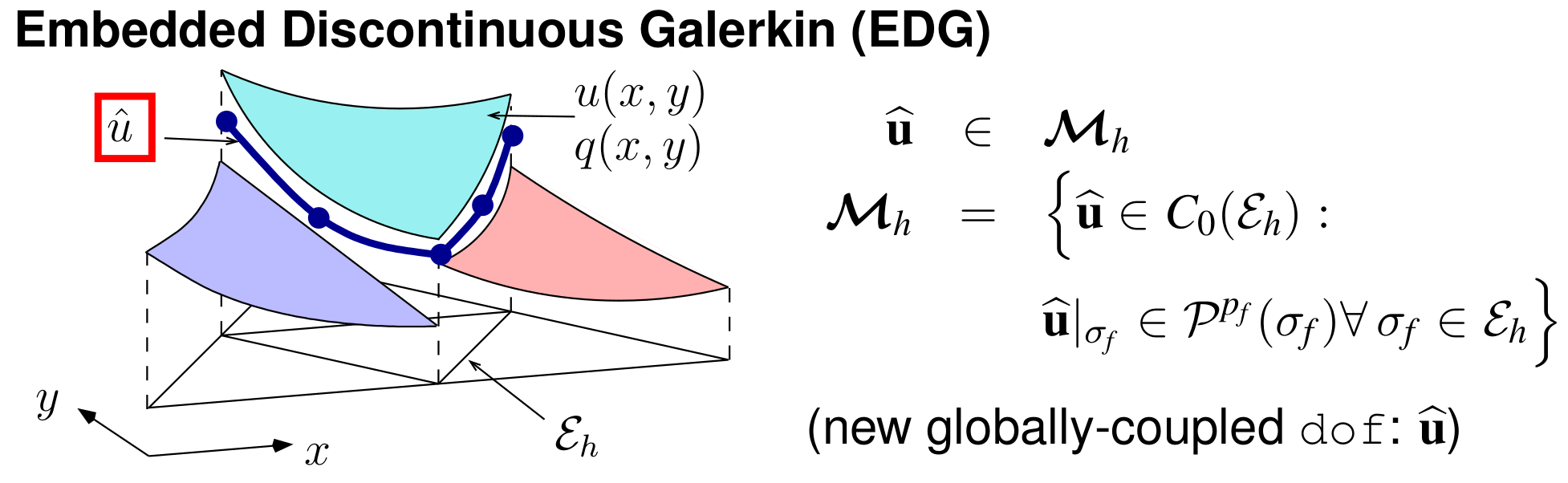
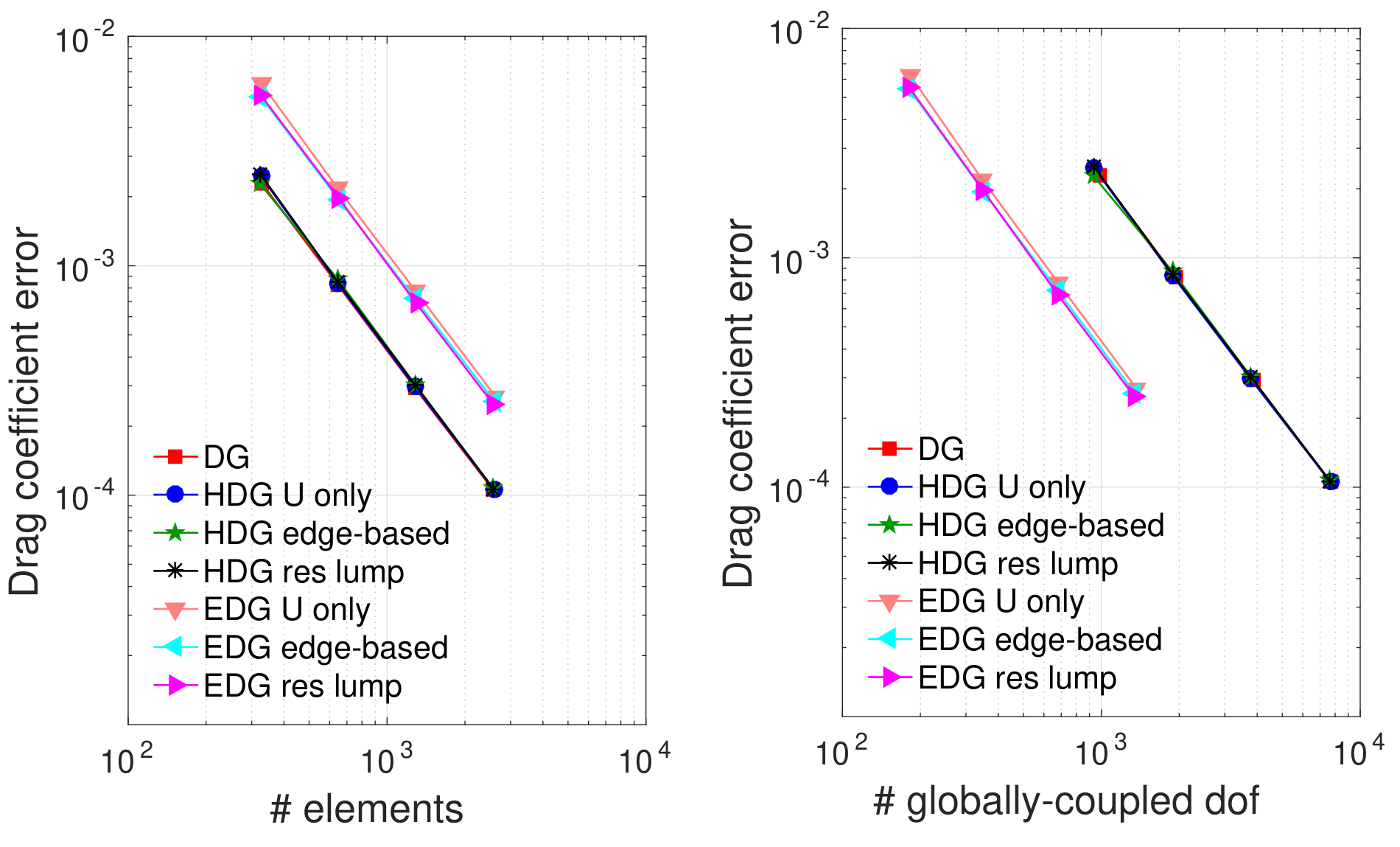
Although discontinuous Galerkin (DG) method have enabled high-order accurate computational fluid dynamics simulations, their memory footprint and computational costs remain large. Two approaches for reducing the expense of DG are (1) modifying the discretization; and (2) optimizing the computational mesh. We study both approaches and compare their relative benefits. Hybridization of DG is an approach that modifies the high-order discretization to reduce its expense for a given mesh. The high cost of DG arises from the large number of degrees of freedom required to approximate an element-wise discontinuous high-order polynomial solution. These degrees of freedom are globally-coupled, increasing the memory requirements for solvers Hybridized discontinuous Galerkin (HDG) methods reduce the number of globally-coupled degrees of freedom by decoupling element solution approximations and stitching them together through weak flux continuity enforcement. HDG methods introduce face unknowns that become the only globally-coupled degrees of freedom in the system. Since the number of face unknowns is generally much lower than the number of element unknowns, HDG methods can be computationally cheaper and use less memory compared to DG. The embedded discontinuous Galerkin (EDG) methodis a particular type of HDG method in which the approximation space of face unknowns is continuous, further reducing the number of globally-coupled degrees of freedom. We have developed mesh optimization approaches for hybridized discretizations. In addition to reducing computational costs, the resulting methods improve (1) robustness of the solution through quantitative error estimates, and (2) robustness of the solver through a mesh size continuation approach in which the problem is solved on successively finer meshes. Ongoing research directions in this are include:- Extension to three dimensions
- Efficient solvers for HDG and EDG
- Application to unsteady problems
 Relevant Publications
Relevant Publications
Krzysztof J. Fidkowski and Guodong Chen. Output‐based mesh optimization for hybridized and embedded discontinuous Galerkin methods. International Journal for Numerical Methods in Engineering, 121(5):867--887, 2019. [ bib | DOI | .pdf ]
Krzysztof J. Fidkowski. A hybridized discontinuous Galerkin method on mapped deforming domains. Computers and Fluids, 139(5):80--91, November 2016. [ bib | DOI | .pdf ]
Back to topOutput-based error estimation and mesh adaptation
Computational Fluid Dynamics (CFD) has become an indispensable tool for aerodynamic analysis and design. Driven by increasing computational power and improvements in numerical methods, CFD is at a state where three-dimensional simulations of complex physical phenomena are now routine. However, such capability comes with a new liability: ensuring that the computed solutions are sufficiently accurate. CFD users, experts or not, cannot reliably manage this liability alone for complex simulations. The goal of this research is to develop methods that will assist users and improve the robustness of these simulations. The two key directions of these research are:- Developing appropriate error estimators using adjoint-based output error calculations.
- Developing robust mesh adaptation strategies for complex geometries.
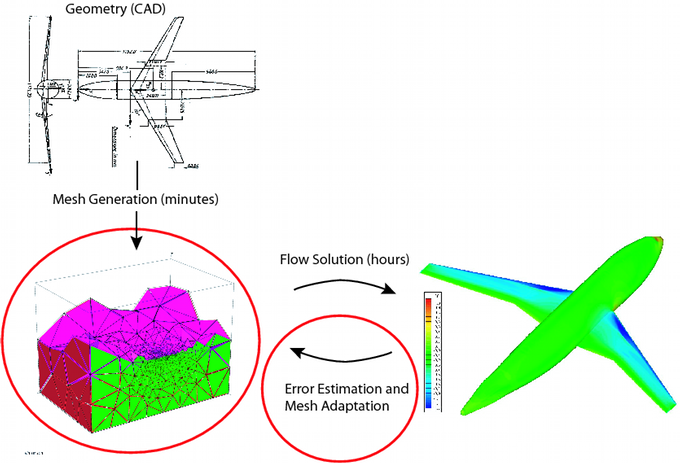 Relevant Publications:
Relevant Publications:
Krzysztof J. Fidkowski and David L. Darmofal. Review of output-based error estimation and mesh adaptation in computational fluid dynamics. AIAA Journal, 49(4):673--694, 2011. [ bib | DOI | .pdf ]
Back to topAdaptive RANS calculations with the discontinuous Galerkin method
The accuracy of aerospace computational simulations depends heavily on the amount of numerical error present, which in turn depends on the allocation of resources, such as mesh size distribution. This is especially true for Reynolds-averaged Navier-Stokes (RANS) calculations, which possess a large range of spatial scales that make a priori mesh construction difficult. In this project a high-order CFD code based on the discontinuous Galerkin discretization is used to adaptively resolve two and three-dimensional RANS cases. Research areas include robust solvers on under-resolved meshes, output-based anisotropy detection, and efficient meshing. Sample results obtained thus far are shown below.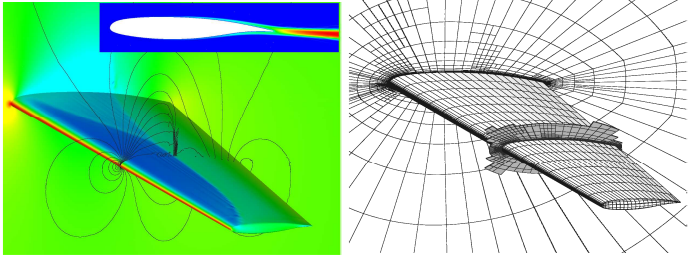
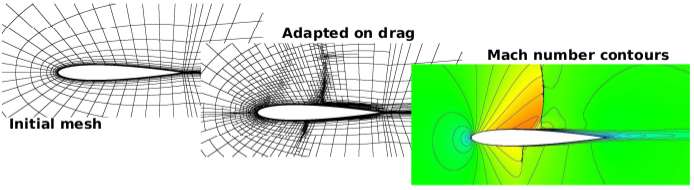
 Relevant Publications and Presentations:
Relevant Publications and Presentations:
M.A. Ceze and K.J. Fidkowski. Output-Driven Anisotropic Mesh Adaptation for Viscous Flows Using Discrete Choice Optimization. AIAA Paper Number 2010-0170, 2010.
Back to topUnsteady output-based adaptation
The objective of this project is to improve the robustness and efficiency of unsteady CFD simulations using adjoint-based adaptive methods. While output error estimation has received considerable attention for steady problems, its application to unsteady simulations remains a challenging problem in computation. This project addresses the theoretical and implementation hurdles of applying output-based methods to unsteady simulations. Topics addressed include development of a suitable variational space-time discretization and solver, solution of the unsteady adjoint problem, and combined spatial and temporal mesh adaptation on dynamic resolution meshes. A sample space-time adaptive result of a gust encounter is shown below.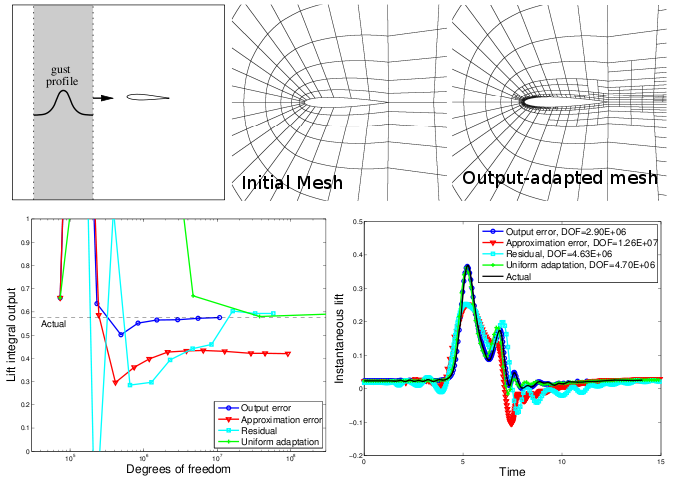 Relevant Publications:
Relevant Publications:
Krzysztof J. Fidkowski and Yuxing Luo. Output-based space-time mesh adaptation for the compressible Navier-Stokes equations. Journal of Computational Physics, 2011.
Back to topEntropy-adjoint approach to mesh refinement
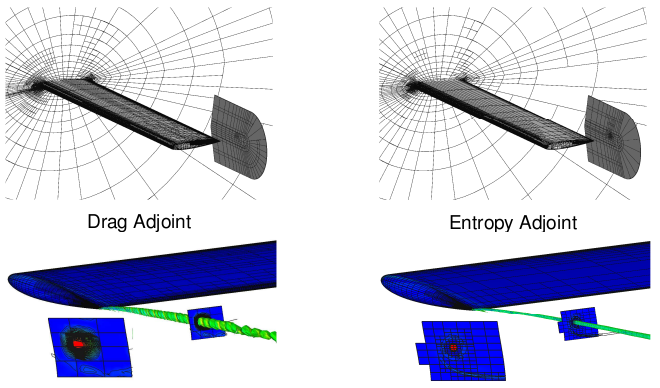
Joint work with Philip Roe When only a handful of engineering outputs are of interest, the computational mesh can be tailored to predict those outputs well. The process requires solutions of auxiliary adjoint problems for each output that provide information on the sensitivity of the output to discretization errors in the mesh. This information guides mesh adaptation, so that after a few iterations of the process, the engineer receives an accurate solution along with error bars for the outputs of interest. However, the extra adjoint solutions add a non-trivial amount of computational work. It turns out for many equations, including Navier-Stokes, there exists one "free" adjoint solution that is related to the amount of entropy generated in the flow. This adjoint is obtained by a simple variable transformation and is therefore quite cheap to implement. An example case adapted using such an entropy adjoint, along with other adaptive indicators for comparison, is presented below. This indicator is particularly well-suited for capturing vortex structures, such as those that persist for extended lengths in rotorcraft problems. Ongoing research is investigating the applicability of the entropy adjoint and to unsteady aerospace engineering simulations.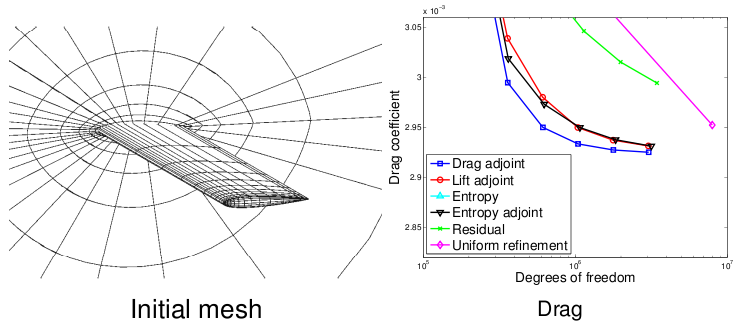
 Relevant Publications:
Relevant Publications:
K.J. Fidkowski, and P.L. Roe. An Entropy Adjoint Approach to Mesh Refinement. SIAM Journal on Scientific Computing, 32(3), 2010, pp 1261-1287.
K.J. Fidkowski, and P.L. Roe.
Entropy-based Refinement I:
The Entropy Adjoint Approach
2009 AIAA Computational
Fluid Dynamics Conference, June 2009.
Contaminant source inversion
Joint work with Karen Willcox, Chad Lieberman, Bart van Bloemen Waanders
The scenario of interest in this project is that of a
contaminant dispersed in an urban environment: the
concentration diffuses and convects with the wind. The
challenge is to use limited sensor measurements to
reconstruct where the profile came from and where it is
going. Such a large-scale inverse problem quickly becomes
intractable for real-time results that could be vital for
decision-making. The animation to the right illustrates a
forward simulation starting from one possible initial
concentration -- the forward problem alone took 1 hour to
run on 32 processors.
Two solution approaches are pursued in this project:
|

|
Deterministic inversion using model reduction
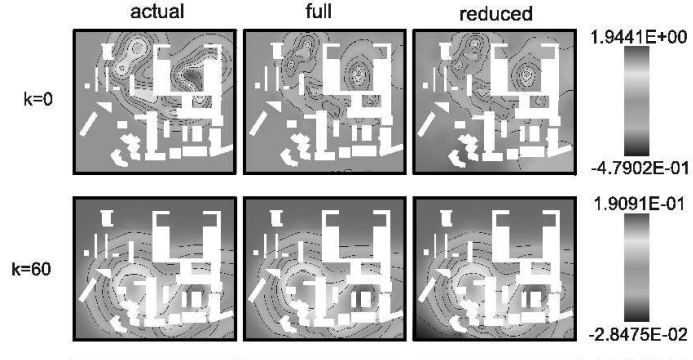
One way to solve the problem in real time is to build a reduced model of the unsteady system. This reduced model (typically a couple hundred unknowns) is then used to invert measured concentrations into an approximation for the initial conditions, which can then be immediately run forward in time for prediction. The time-consuming model reduction can be run ahead of time on a supercomputer, while the real-time inversion can be performed with the reduced model on laptops in the field. Shown below is a comparison between true and inverted (using the full and reduced models) initial conditions for a sample problem in which full time histories from 36 randomly-placed sensors were used to invert for the initial concentration field.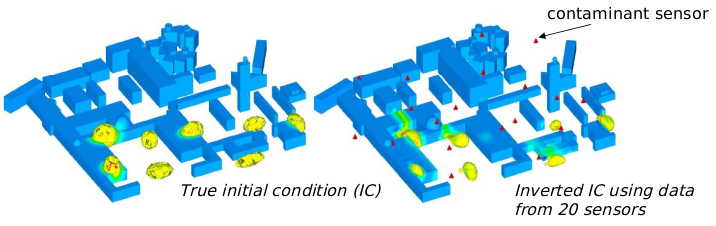
Statistical inversion with adjoint-based output calculation.
Single-point deterministic inverse calculations can be ill-conditioned when the measurement data are limited. More robust in such cases is a probabilistic approach that provides statistical information about where the contaminant could have originated. However, obtaining this information generally requires a very time consuming sampling process. The goal of this work is to dramatically speed up the probabilistic inversion by combining Markov-chain Monte Carlo (MCMC) sampling with adjoint-based output calculations. A probabilistic inversion result is shown below in terms of MCMC sample traces for the same geometry as discussed above. The inverse calculation assumed one contaminant source with an unknown position. The calculation of tens of thousands of samples was rapid enough to be performed in real time.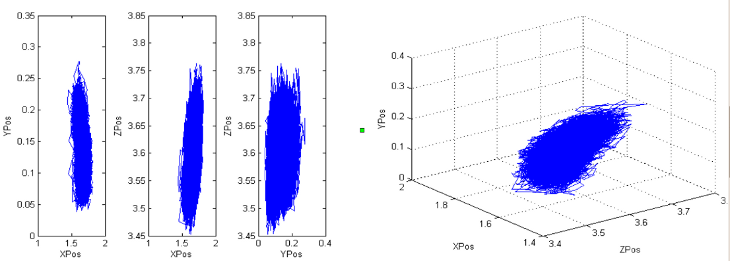 Relevant Publications and Presentations:
Relevant Publications and Presentations:
C. Lieberman, K. Fidkowski, K. Willcox, and B. van Bloemen Waanders. Hessian-based model reduction: large-scale inversion and prediction. International Journal for Numerical Methods in Fluids, 2012. [ bib | DOI | .pdf ]
Back to topCut-cell meshing
Mesh generation around complex geometries can be one of the most time-consuming and user-intensive tasks in practical numerical computation. This is especially true when employing high-order methods, which demand coarse mesh elements that have to be shaped (i.e. curved) to represent surface features with an adequate level of accuracy. Requirements of positive element volumes and adequate geometry fidelity are difficult to enforce in standard boundary conforming meshes.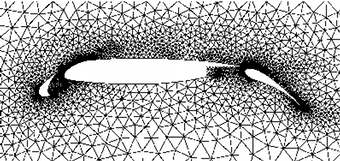
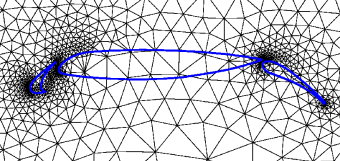
| Boundary-conforming mesh | Cut-cell mesh |
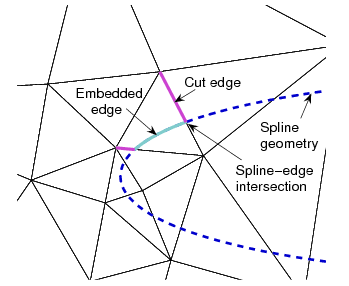
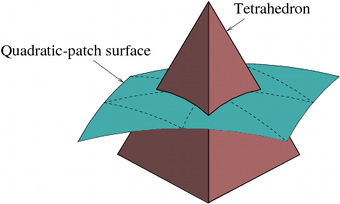 For the geometry, splines are used in 2D and curved triangular
patches are used in 3D, as illustrated above. Key to the
success of the DG high-order finite element is element
integration rules, which are derived automatically using Green's
theorem. Triangular and tetrahedral background elements are
used as they can be stretched to resolve anisotropic features.
For the geometry, splines are used in 2D and curved triangular
patches are used in 3D, as illustrated above. Key to the
success of the DG high-order finite element is element
integration rules, which are derived automatically using Green's
theorem. Triangular and tetrahedral background elements are
used as they can be stretched to resolve anisotropic features.

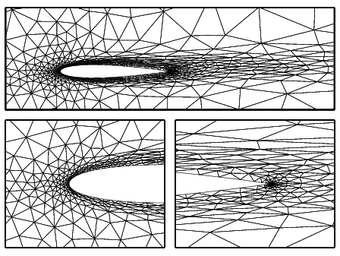
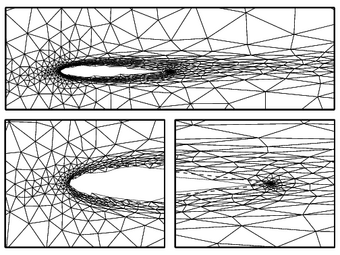
 Shown above are Mach number contours from a subsonic Euler
simulation around a wing-body configuration. 10,000 curved
surface patches were used to represent the geometry and the
final, solution-adapted background mesh for a p=2
solution contained 85,000 elements. Below are
boundary-conforming and cut-cell meshes from a viscous
simulation over an airfoil. Anisotropic mesh refinement was
driven by a drag output error estimate.
Shown above are Mach number contours from a subsonic Euler
simulation around a wing-body configuration. 10,000 curved
surface patches were used to represent the geometry and the
final, solution-adapted background mesh for a p=2
solution contained 85,000 elements. Below are
boundary-conforming and cut-cell meshes from a viscous
simulation over an airfoil. Anisotropic mesh refinement was
driven by a drag output error estimate.
| Boundary-conforming mesh | Cut-cell mesh |
K.J. Fidkowski and D.L. Darmofal. A triangular cut–cell adaptive method for high–order discretizations of the compressible Navier–Stokes equations. Journal of Computational Physics. 225, 2007, pp 1653-1672.
K.J. Fidkowski and D.L. Darmofal. An adaptive simplex cut–cell method for discontinuous Galerkin discretizations of the Navier–Stokes equations. AIAA Paper Number 2007-3941, 2007.
Back to topNonlinear model reduction for inverse problems
Joint work with Karen Willcox, David Galbally In model reduction, a large parameter-dependent system of equations is replaced by a much smaller system that accurately approximates outputs over a certain range of parameters. Many systematic techniques exist for performing such reduction; this work used standard Galerkin projection with proper orthogonal decomposition (POD) for basis construction. To treat the nonlinearity efficiently, a masked-projection technique (similar to gappy POD, missing point estimation, and coefficient function approximation) was used.
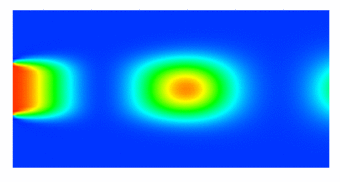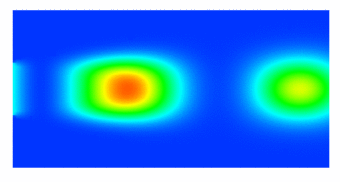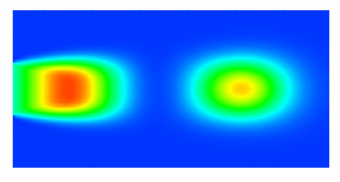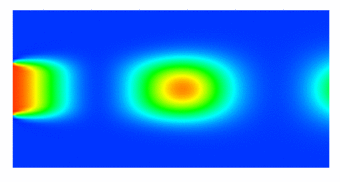
|
To demonstrate the model reduction technique, a scalar convection-diffusion-reaction problem was considered. The scenario consists of fuel injected into a combustion chamber and left to react with a surrounding oxidizer as it convects downstream. A 2D unsteady simulation is shown at left, for a pulsating injection concentration. Reduction of a steady 3D combustion chamber was performed in parallel, reducing the degrees of freedom (DOF) from 8.5 million to 40. Sample fuel concentration profiles are illustrated below. |
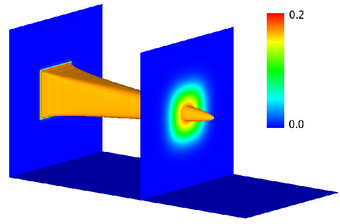
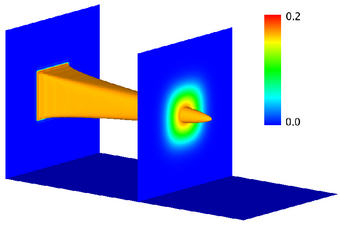
| Full system: 8.5 million DOF, 13h CPU time | Reduced system: 40 DOF, negligible CPU time |
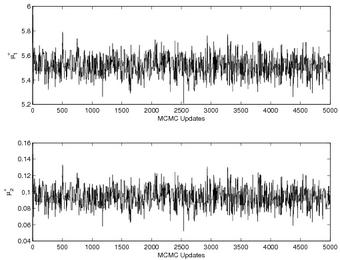
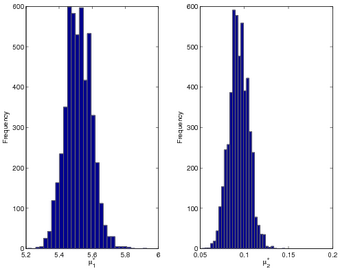
| MCMC samples | Posterior histogram |
D. Galbally, K. Fidkowski, K. Willcox, and O. Ghattas, Nonlinear Model Reduction for Uncertainty Quantification in Large-Scale Inverse Problems. International Journal for Numerical Methods in Engineering. 81(12), 2009, pp 1581-1603.
Nonlinear Model Reduction for
Uncertainty Quantification in Large-Scale Inverse
Problems
Computational Aerospace Sciences Seminar,
October 2008.