Ogilvie Group

2D Electronic Spectroscopy
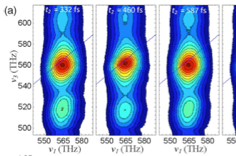
The techniques of multidimensional Fourier transform spectroscopy have revolutionized nuclear magnetic resonance (NMR), making it an invaluable tool for determining high resolution structures of complicated biomolecules. NMR can also study dynamics, but on limited time scales. Two dimensional electronic spectroscopy (2DES) is the optical analog of the simplest multidimensional NMR experiment. In analogy to 2D NMR, the 2DES spectrum reveals the coupling between electronic transitions, which appear as cross-peaks. The underlying lineshapes, describing the system dynamics are also revealed in the 2D spectrum, free from inhomogeneous broadening. Our group has been working to make 2DES a simple and accessible technique, and to expand the information content of 2DES for applications to understanding natural and artificial light-harvesting.
2DES with a pulse-shaper
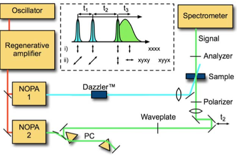
One of the major obstacles to performing 2DES is attaining phase sensitive detection of the signal field, which requires nanometer-scale stability in the optical paths used in the experiment. A diffractive-optics-based approach can solve this problem (read about it here). An alternative is to use a pulse-shaper to produce pulse-pairs that are accurately timed and have relative phase control (read about it here). This approach can be used in the “pump-probe” geometry, allowing for easy alignment and conversion of standard pump-probe experiments to 2DES. Phase-cycling offers some useful possibilities for separating different nonlinear signals and removing scatter.
2DES with a continuum probe
The information content available in a 2D spectrum is limited by the bandwidth of the exciting and probing beams. However, many natural and artificial light-harvesting systems absorb broadly from the UV to the near infrared. To allow the study of energy and charge transfer events spanning the visible and near-IR spectrum we have implemented 2DES with a continuum probe. We’ve used the large bandwidth to study the effects of vibrational wavepacket dynamics on 2D spectra (read about it here).