The Great Ball Drop Experiment

Shinichiro Sakaki and Lavell Blanchard
Physics 1999 Final Project
Mr. Matthew T. Geyman

Purpose:

The purpose of this project is to see if the "Ball and Cup" trick outlined in our textbook (Physics; 3rd Edition; by Wilson & Buffa; Prentice Hall) truly works and if the angle of the top board and the weight of the top board will cause a change in the results of the trick, and to see if the ideas of Galileo hold true in this experiment.

Procedure:

Back to Table of Contents

---

Apparatus:

3 sticks (48 inches, 46 inches and 23 inches) 2 golf ball (Spalding, Top-flite plus II) 2 Spring water cups cut in half carpenter's square 2 hinges silly putty clay 1 Egg exact knife video camera 2 chop sticks pen , pencil paper protractor spot light

ÝBack to Table of Contents

Measurements:

Test 1:  Changing the angle

Result:  The ball did not go into the cup at the angle less than 30 degree and the angle more than 45 degree.

Test 2:  Adding weight to the middle of the top-board.  Same size cup used as Test 1.

Result: we got the same results as Test 1 even when we added weight to the middle of the top-board.  We tested with 100g and 200g of weight.

Test 3: Changing the angle using a shallower cup

Result: after making the height of the cup smaller, range of the angle increased.  From minimum of 20 degreeto maximum of 55 degree.  Between 30 degree and 45 degree, we obtained same result as Test 1

Calculations:ÝÝ

B = H Cos(angle)

or

Base length = 46 inches Cos (angle)

therefore

X (ball-cup distance) = H (46 inches) ó B ( base)

Calculated Results:

Actual working differences between ball-cup distances for 5 degree angles
    7.25 inches -5.50 inches = 1.75 inches
    9.00 inches - 7.25 inches = 1.75 inches
    10.75 inches - 9.00 inches = 1.75 inches
 

    3.5 inches - 2.5 inches = 1.0 inches
    15 inches -14 inches =1 inch

Back to Table of Contents

Conclusion:

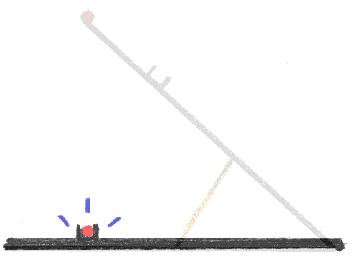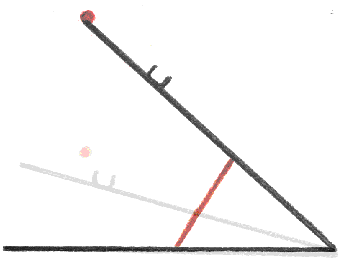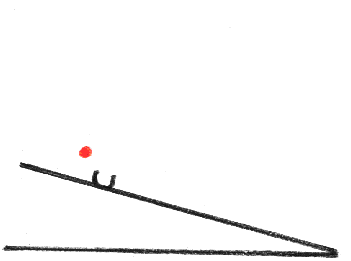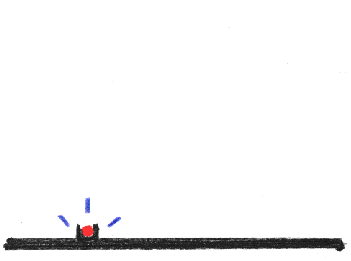
The ball, when sitting on the propped up top-board, is at a greater height than the cup that is attached to the board; still, when the stick is removed and the ball and cup are falling, the ball lands in the cup.  The ball falls in a verticle line, and the cup travels in an arc to the same spot.  Even though the board and cup are moving in a circular path, it appears that board and the cup are accelerating faster than the ball, causing the board to hit the ground before the ball ó but this would contradict the ideas of Galileo Galilei and his law of falling objects, which states that all objects fall at the same rate due to the gravitational force applied to them.  However the board, in this case, is not free-falling.  One end of it is already on the ground.  As the starting angle between the ground and the top-board decreases, the board's rate of acceleration will approach (but never quite reach) 9.8 meters per second squared.  The top-board with the cup and the ball drop at almostthe same rate of acceleration; the cup starts slightly lower than the ball, and simply arrives first due to this starting height difference alone.

In Test 2, even though we knew better, we assumed that weight would affect the top-board's falling rate before we start the experiment.Ý However, as you can see from the results, weight will not affect the falling acceleration of the top-board.ÝIf the top-board fell faster, the range of working angles would increase, but since the range of the angle did not increase in Test 2, we can say that the falling speed of the board didn't increase even though we added weights.  It means this experiment is still follows Galileo's principal of free fall ó weight has nothing to do with the rate of free fall.

The range of angles for a top-board length 46 inches with a cup height of 2.5 inches is greater than 30 degrees but less than 45 degrees.Ý If you make the angle smaller, the ball will hit the cup and will not go in. Also if the angle exceeds 45 degrees, the ball will hit the side of the cup.Ý This means that the cup is too high and needs to be shallower in order for the ball to go in.Ý When we tested with a shallower cup, 1.5 inches high, the range of angles increased, from a minimum of 20 degrees to a maximum of 55 degrees.Ý From that we can conclude that with the same length top-board, the height of the cup is the most important factor for determining the range of angles for the test to work.  If the top-board is at a much greater angle, this difference in falling acceleration prevents the ball from dropping into the cup ó the ball would end up rolling down the board.  If the top-board were at a much lower angle, the arc would not produce enough horizontal movement to move the cup under the ball, and the cup would have to be extremely short as well.

We can conclude that, within the range of operating angles (30 - 45 degrees), there is a direct relation between angle and distance between the ball and the cup; for every 5 degree change in angle, the distance must change about 1.75 inches in the corresponding direction.  Also, between the angles of 20 and 30 degrees, and between 45 and 55 degrees, the distance between the ball and the cup increases 1 inch for every 5 degrees.

There is one remaining aspect of The Great Ball Drop Experiment to be considered:  The "Coolness Proportion:"  This experiment is neat because it appearsunlikely.  In fact, the more unlikely it appears, the cooler it is.  And the way that it looks most unlikely is when the top edge of the cup is at the nearest possible height to the bottom of the ball (of course, it can never be higher).   Therefore:

For a cup of given height, the Coolness is greatest at the lowest operational angle, or  Given cH, C is inversly proportional to A until failure.

 So, we determined that given a cup height of 2.5 inches, the Coolness was greatest at 30 degrees.
 

And finally, what we're sure you are waiting for is to see this phenomenon in action!

Back to Table of Contents