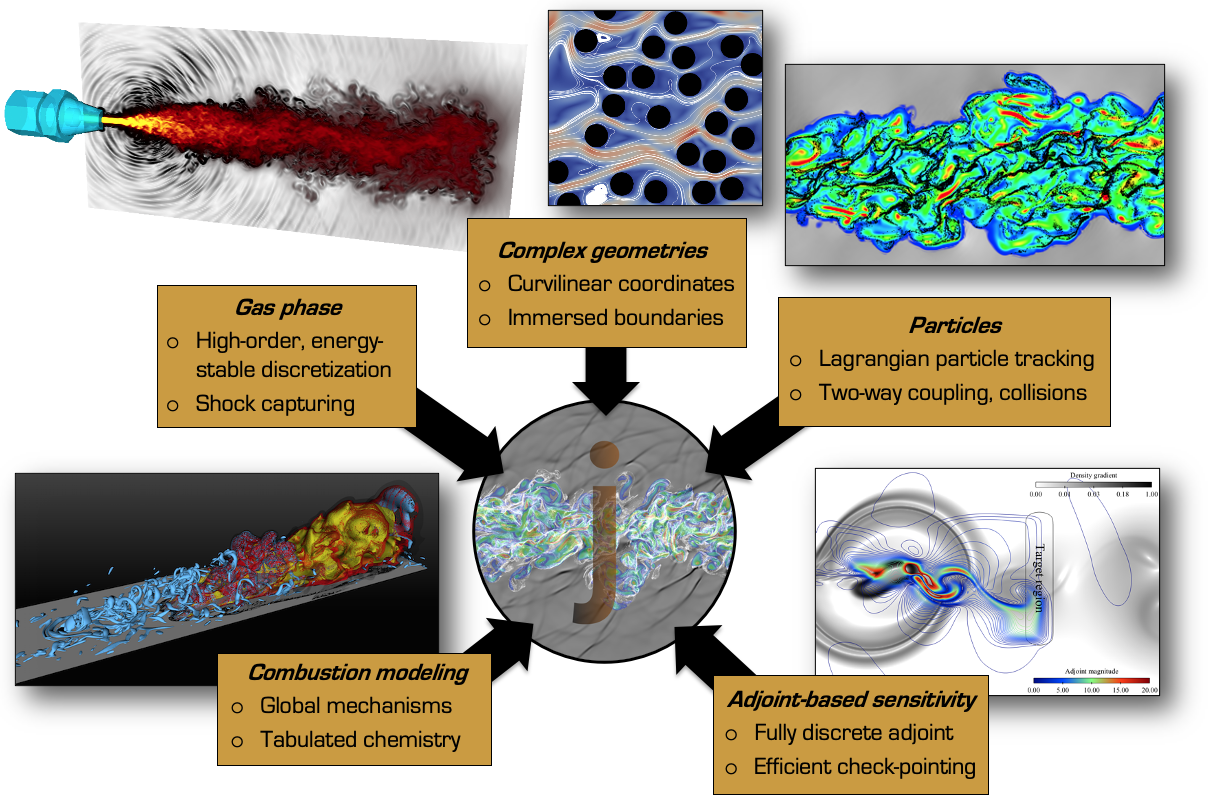
Specific features:
jCODE consists of a number of modules for simulating high-speed
(compressible) two-phase and chemically reacting flows in complex geometries, and corresponding adjoint-based sensitivity. Specific features include:
High-order narrow stencil finite difference operators that satisfy
summation-by-parts (SBP) property
Simultaneous-approximation-term (SAT) boundary treatment to
ensure an energy estimate
A characteristic-based immersed boundary method for efficienty
handling complex geometries on structured grids for inviscid and
viscous flows
Lagrangian particle tracking capabale of simulating upwards of a
billion individual particles undergoing mass/momentum/heat exchange
and inter-particle collisions
Fully discrete adjoint capabilities to provide machine-precision
sensitivity for turbulent reacting flows
|
|
Parallel performance:
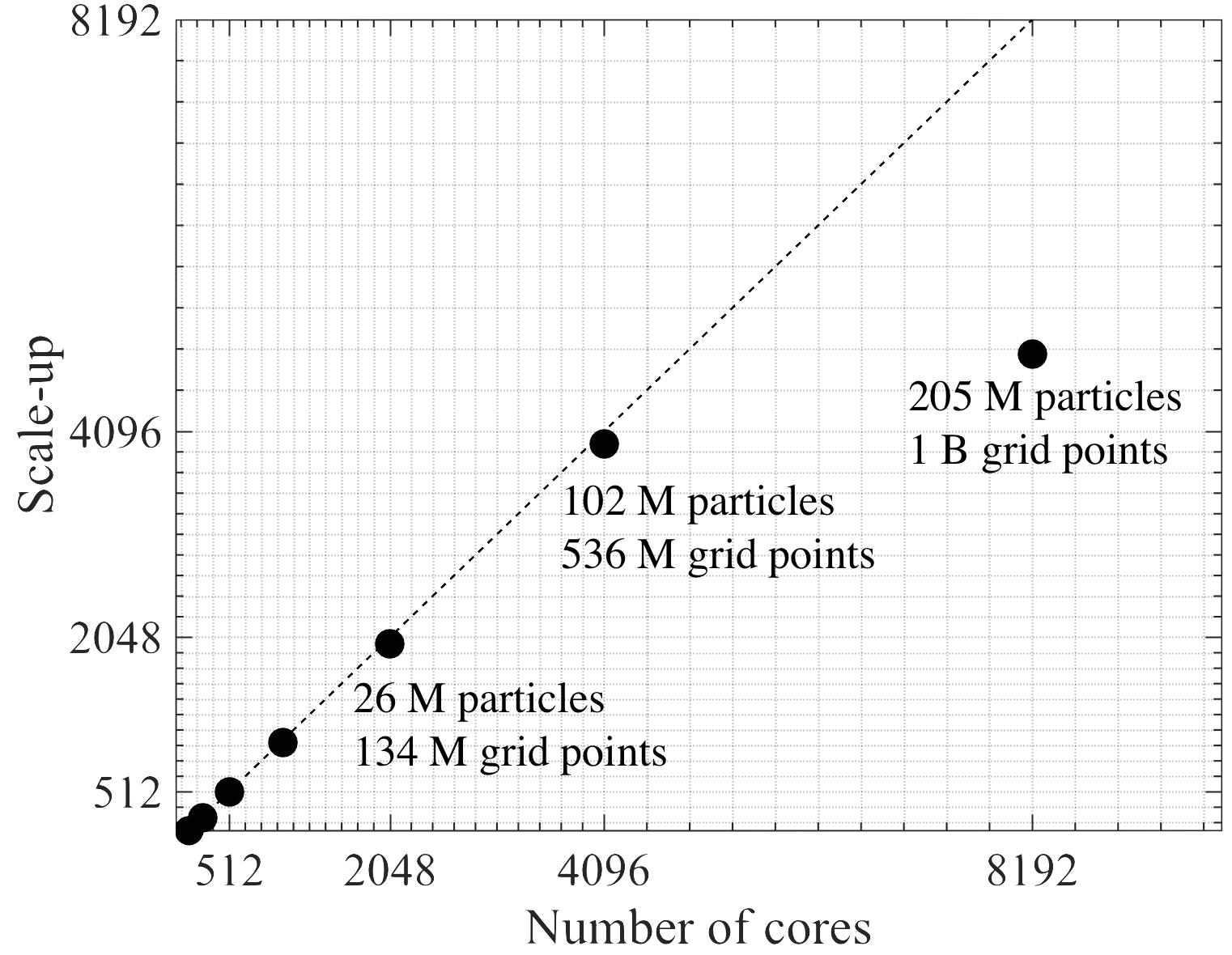
Scale-up of jCODE on OLCF Titan. The code is
fully explicit and massively parallel, enabling large-scale
computations with billions of grid points and 100s of millions of
particles.
|
|