Flow Equation Formalism Applied to Class of Dark Energy Models

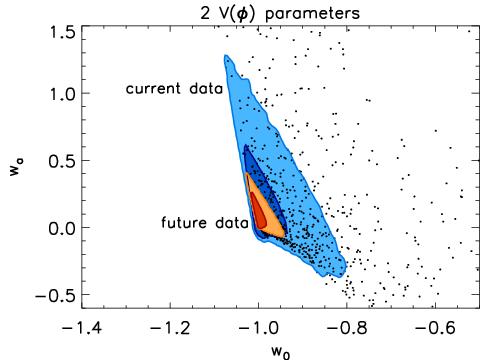
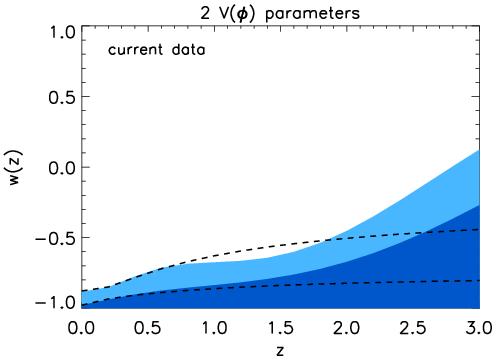
original parameters w(z) histories w0-wa constraints w(z) reconstruction thawing/freezing

This web page contains data relevant to the paper

"Dynamical behavior of generic quintessence potentials: constraints on key dark energy observables"

by D. Huterer and H.V. Peiris ( Phys. Rev. D 75, 083503 (2007), astro-ph/0610427). High resolution figures from the paper are available here.


Below we provide Markov Chains with scalar field model parameters.

For each class of models and (current or future) cosmological data, there are are four chains (in four files) contained in a .tar.gz tarball. For each class, there are additional four files that contain the w(z) history for each model. The classes of models we have assumed are 2 and 3-parameter V(&phi) models with either current or future data.

The Files

2 parameter V(&phi), current data (75 Mb file):

  • chains_2param.tar.gz

    2 parameter V(&phi), future data (67 Mb file):
  • chains_2param_future.tar.gz

    3 parameter V(&phi), current data (56 Mb file):
  • chains_3param.tar.gz

    3 parameter V(&phi), future data (92 Mb file):
  • chains_3param_future.tar.gz
    File Format

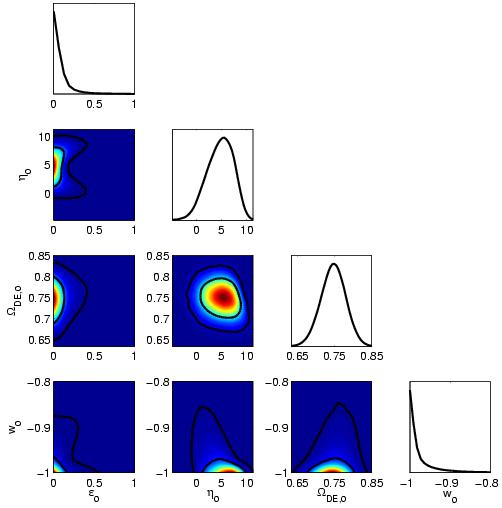
    Columns are, for the 2-V(&phi)-parameter case (these parameters, for each model, are written in a single row)


    weight, -ln(Likelihood)
    &epsilon(3), &eta(3), &OmegaDE(3), w(3), &thetaA, &Omegabh2,
    &epsilon(0), &eta(0), &OmegaDE(0), w(0), &thetaA, &Omegabh2,
    &alpha1, &alpha2, &alpha3,
    w0, wa

    where the parentheses show whether the parameter was evaluated at z=3 (our starting redshift) or z=0. Here &epsilon and &eta are the two "slow-roll" parameters (note they are not necessarily small for DE), and &OmegaDE, and w are energy density and equation of state of DE. Further, &thetaA and &Omegabh2 are the CMB angle subtended by the first peak (in degrees) and baryon fraction respectively; note they are repeated twice in the files. Finally, &alphai (i=1, 2, 3) are the first three principal components of the equation of state, while w0 and wa are derived from the PCs as described in the paper.

    For the 3-V(&phi)-parameter case there is one extra parameter, the third "slow-roll" parameter &xi and the format is now


    weight, -ln(Likelihood)
    &epsilon(3), &eta(3), &OmegaDE(3), w(3), &thetaA, &Omegabh2 &xi(3),
    &epsilon(0), &eta(0), &OmegaDE(0), w(0), &thetaA, &Omegabh2 &xi(0),
    &alpha1, &alpha2, &alpha3,
    w0, wa


    Finally, for the "_wz" files the format is


    weight, -ln(Likelihood), w(0.0), w(0.2),... w(3.0)


    where w(z) refers to value of the equation of state at redshift z in each model.

    Usage of chains

    While we give the likelihood of individual models for reference, the posterior must be calculated using the weights of the models which are proportional to the PDF (Bayes Theorem). Our chains are fully compatible with the GetDist parameter estimation package, supplied as part of cosmomc, with minor modifications to the parameter file to change the variable names to those that we use.

    Dragan Huterer