Algorithm development & Monte Carlo methods
A large part of our activities is the design and implementation of new numerical methods. In particular we work on `diagrammatic’ or `continuous-time’ methods for quantum impurity and lattice models. These algorithms are based on a diagrammatic expansion of the system’s partition function, and they are by now the methods of choice for solving quantum impurity models.
Example 1: Continuous-time Auxiliary Field Algorithm
The continuous-time auxiliary field algorithm is based on the partition function expansion of an impurity model into a `weak coupling’ series, coupled with an auxiliary field decomposition. The algorithm can be applied to any Hamiltonian with density - density interactions. Similarly to the stochastic ‘flipping of spins’ in a simple Ising simulation, the algorithm is based on the stochastic insertion and removal of diagrams’ in a diagrammatic configuration space. Here is an illustration of a CT-AUX update: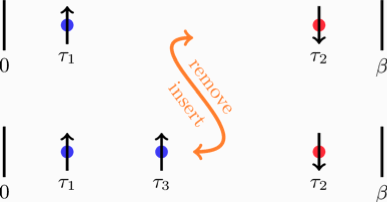
The picture shows that a vertex (with blue spin) is either inserted or removed, resulting in a diagram of 2nd (for removal) or 3rd (for insertion) order.
Because it is numerically exact and because it is substantially faster than other algorithms, CT-AUX is ideally suited to the simulation of large impurity clusters.
Example 2: Bold Diagrammatic Monte Carlo out of equilibrium
Out of equilibrium, on the Keldysh contour, most of our numerically exact algorithms fail. Standard Monte Carlo methods run in to a sign problem, NRG methods converge slowly, and DMRG methods can only access short times. It makes therefore sense to build numerical methods on top of analytic methods that already contain an important part of the physics. This is the idea of the `Bold’ methods, which combine an approximate analytical solution with a numerical correction that recovers the exact solution.
By combining NCA and OCA perturbation theory methods with diagrammatic Monte Carlo techniques, BoldNCA can reach much longer times out of equilibrium than previously accessible. The reason is a reduced `dynamic’ sign problem coming from the inclusion of diagrams in the NCA/OCA methods.
Here is an illustration of a BoldNCA diagram on the Keldysh contour:

The ‘bold’ lines signify propagators that already contain an infinite number of diagrams.
Relevant Publications
Voltage Quench Dynamics of a Kondo System
Andrey E. Antipov, Qiaoyuan Dong, and Emanuel Gull
Phys. Rev. Lett. 116, 036801 (2016)
Taming the Dynamical Sign Problem in Real-Time Evolution of Quantum Many-Body Problems
Guy Cohen, Emanuel Gull, David R. Reichman, and Andrew J. Millis
Phys. Rev. Lett. 115, 266802 (2015)
Green's functions from real-time bold-line Monte Carlo
Guy Cohen, David R. Reichman, Andrew J. Millis, and Emanuel Gull
Phys. Rev. B 89, 115139 (2014)
Continuous-time Monte Carlo methods for quantum impurity models,
Emanuel Gull, Andrew J. Millis, Alexander I. Lichtenstein, Alexey N. Rubtsov, Matthias Troyer, Philipp Werner.
Rev. Mod. Phys. 83, 349 (2011).