Find \(R,t\) such that
\[
q_i = Rp_i + t
\]
Problem statement
Find \(R,t\) such that
\[
q_i = Rp_i + t
\]
Problem statement
From robots point of view
Related work
Single observation
External landmarks
Egomotion
- No mutual observation.
- Example: ARToolKit (Kato et al. 1999)
- Controlled environment.
- Corner features are error prone.
- Example: Bundler (Snavely et al. 2006)
- Needs accurate egomotion estimates.
Mutual localization
A generalized Perspective-N-Point algorithm
Mutual localization
Using minimum fiducials
Mathematical formulation
\[
\newcommand{\vect}[1]{\mathbf{#1}}
\newcommand{\hvect}[1]{\bar{\vect{#1}}}
\newcommand{\uvect}[1]{\hat{\vect{#1}}}
\newcommand{\field}[1]{\mathbb{#1}}
\]
\begin{align}
\|s_1\uvect{p}_1-s_2\uvect{p}_2\| &=\| \vect{q_1}- \vect{q_2}\| \\
\end{align}
\begin{align}
\|s_2\uvect{p}_2- \vect{p_3}\| &=\| \vect{q_2}-s_3\uvect{q}_3\| \\
\| \vect{p_3}-s_1\uvect{p}_1\| &=\|s_3\uvect{q}_3- \vect{q_1}\|
\end{align}
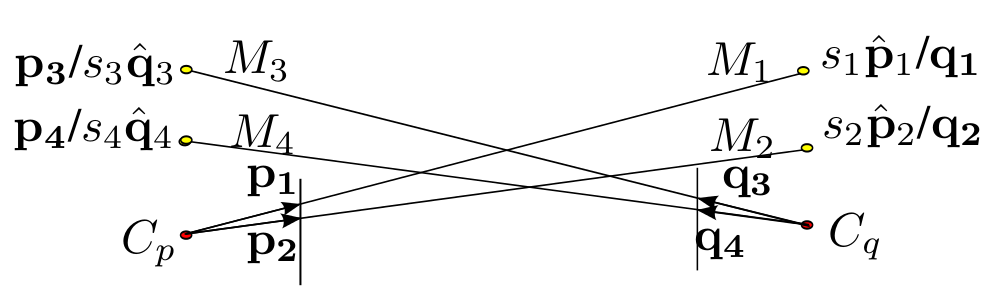
Solving for \(s_1\) \(s_2\) and \(s_3\)
Expanding to polynomials
\begin{align} s_1^2 + s_2^2 - 2s_1s_2\uvect{p}_1^\top\uvect{p}_2 - \|\vect{q}_1 - \vect{q}_2\|^2 &= 0 \\ % s_2^2 - s_3^2 - 2s_2\uvect{p}_2^\top\vect{p}_3 + 2s_3\vect{q}_2^\top\uvect{q}_3 + \|\vect{p}_3\|^2 - \|\vect{q}_2\|^2 &= 0 \\ % s_1^2 - s_3^2 - 2s_1\uvect{p}_1^\top\vect{p}_3 + 2s_3\vect{q}_1^\top\uvect{q}_3 + \|\vect{p}_3\|^2 - \|\vect{q}_1\|^2 &= 0 \label{eq31} \end{align}
\begin{align} s_2^2 + \underbrace{(-2s_1\uvect{p}_1^\top\uvect{p}_2)}_{a_1}s_2 + \underbrace{(s_1^2 - \|\vect{q}_1 - \vect{q}_2\|^2)}_{a_0} = 0 \\ s_2^2 + \underbrace{(-2\uvect{p}_2^\top\vect{p}_3)}_{b_1}s_2 - \underbrace{(s_3^2 - 2s_3\vect{q}_2^\top\uvect{q}_3 - \|\vect{p}_3\|^2 + \|\vect{q}_2\|^2)}_{b_0} = 0 \end{align}
Eliminating \(s_2\)
\begin{align} s_2^2 + \underbrace{(-2s_1\uvect{p}_1^\top\uvect{p}_2)}_{a_1}s_2 + \underbrace{(s_1^2 - \|\vect{q}_1 - \vect{q}_2\|^2)}_{a_0} = 0 \\ s_2^2 + \underbrace{(-2\uvect{p}_2^\top\vect{p}_3)}_{b_1}s_2 - \underbrace{(s_3^2 - 2s_3\vect{q}_2^\top\uvect{q}_3 - \|\vect{p}_3\|^2 + \|\vect{q}_2\|^2)}_{b_0} = 0 \end{align}
- \begin{align} r(s_1, s_3) = \begin{vmatrix} 1 & a_1 & a_0 & 0 \\ 0 & 1 & a_1 & a_0 \\ 1 & b_1 & b_0 & 0 \\ 0 & 1 & b_1 & b_0 \end{vmatrix} = 0 \label{eq:sylvester} \end{align}
Eliminating \(s_3\)
\begin{equation} \begin{split} r(s_1, s_3) = c_4s_3^4 + c_3s_3^3 + c_2s_3^2 + c_1s_3 + c_0 &= 0\\ -s_3^2 + \underbrace{(2\vect{q}_1^\top\uvect{q}_3)}_{d_1}s_3 + \underbrace{s_1^2 - 2s_1\uvect{p}_1^\top\vect{p}_3 + \|\vect{p}_3\|^2 - \|\vect{q}_1\|^2}_{d_0} &= 0 \end{split} \end{equation}
- \begin{align} r_2(s_1) = \begin{vmatrix} c_4 & c_3 & c_2 & c_1 & c_0 & 0 \\ 0 & c_4 & c_3 & c_2 & c_1 & c_0\\ 1 & d_1 & d_0 & 0 & 0 & 0 \\ 0 & 1 & d_1 & d_0 & 0 & 0 \\ 0 & 0 & 1 & d_1 & d_0 & 0 \\ 0 & 0 & 0 & 1 & d_1 & d_0 \end{vmatrix} = 0. \label{eq:finalsylvester} \end{align}
Too many roots
Out of the eight roots, only one is right. Which one?
Choosing the optimal root
\(\uvect{p}_1^\top\vect{p}_3 \)
\begin{align*}
s_2 - \uvect{p}_2^\top\vect{p}_3 &> 0\\
s_3 - \vect{q}_2^\top\uvect{q}_3 &> 0\\
s_1 - \uvect{p}_1^\top\vect{p}_3 &> 0\\
\end{align*}
\begin{align}
(s_1 + s_2)^2& - 2s_1s_2(1 + \uvect{p}_1^\top\uvect{p}_2) - \|\vect{q}_1 -
\vect{q}_2\|^2 = 0
\end{align}
\begin{align}
(s_2 - \uvect{p}_2^\top\vect{p}_3)^2
- (s_3 - \vect{q}_2^\top\uvect{q}_3)^2
+ (\vect{p}_3 - \uvect{p}_2)^\top\vect{p}_3
- \vect{q}_2^\top(\vect{q}_2 - \uvect{q}_3) = 0\\
\end{align}
\begin{align}
(s_1 - \uvect{p}_1^\top\vect{p}_3)^2
- (s_3 - \vect{q}_1^\top\uvect{q}_3)^2
+ (\vect{p}_3 - \uvect{p}_1)^\top\vect{p}_3
- \vect{q}_1^\top(\vect{q}_1 - \uvect{q}_3) = 0\\
\end{align}
What about more markers?
- For four markers solve polynomial .
- For more than 5 markers, we can use the homography method. \begin{align*} \vect{q}_i^\top E \uvect{p}_i &= 0 & \forall i \in {1, 2}\\ \uvect{q}_i^\top E \vect{p}_i &= 0 & \forall i \in {3, 4, 5} \label{eq:essentialmatrix} \end{align*}
- For more than 8 markers, the system becomes linear.
Stability against noise
Experimental setup
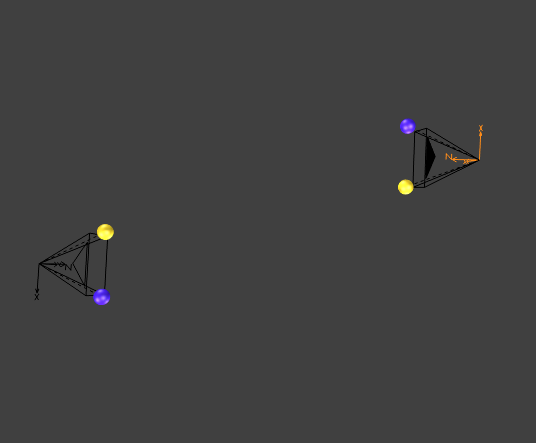
Stability against noise
Results
Experimental setup: Fiducial markers on turtlebot
Experimental setup
Robot placement
Experimental results
Translation error
Experimental setup
Realtime mutual localization
Conclusion
- Localization using fiducial without egomotion
- Generalization of Perspective-N-point algorithm
- Compared accuracy against state of art methods
- Source code and data is available at buffalo.edu/~vikasdhi/
Questions?
Thank You for listening !
Acknowledgements
This material is based upon work partially supported by the Federal Highway Administration under Cooperative Agreement No. DTFH61-07-H-00023, the Army Research Office (W911NF-11-1-0090) and the National Science Foundation CAREER grant (IIS-0845282). Any opinions, findings, conclusions or recommendations are those of the authors and do not necessarily reflect the views of the FHWA, ARO, or NSF.
Reconstruction experiment
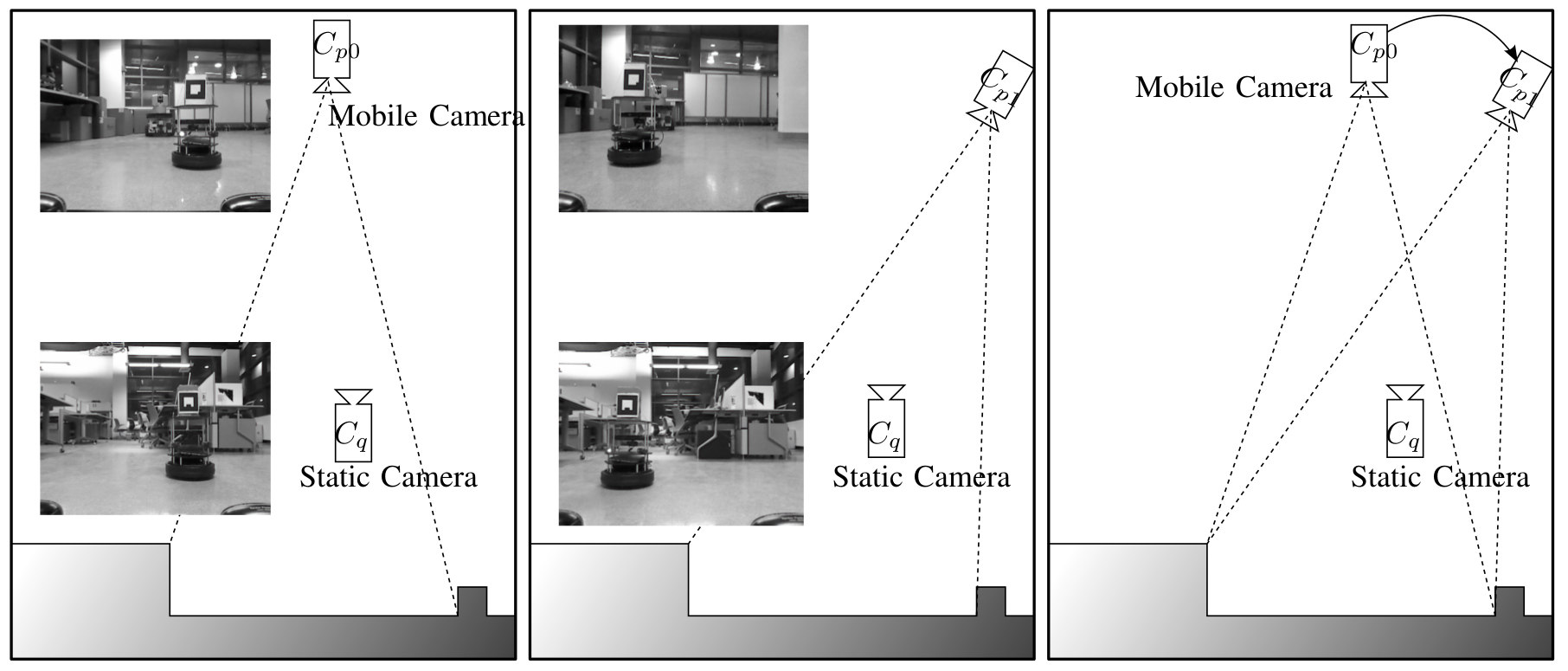
Reconstruction experiment
