David
Stapleton
CV


current teaching: current teaching:
Math 732: Topics in Algebraic Geometry: Cubic Hypersurfaces
previous course websites:
S23:ToA · S22:AGII · F21:Calc1 · S20:Calc3 · F20:Calc3
I am a postdoc in algebraic geometry at the University of Michigan. I was previously a postdoc at UC San Diego and I received my PhD from Stony Brook University.
|
pdf arxiv |
The fibering genus of Fano hypersurfaces,
joint with Nathan Chen, Benjamin Church, and Lena Ji. submitted (2023). |
 |
|
|
pdf
arxiv |
The minimal fibering degree of a toric variety equals the
lattice width of its polytope,
joint with Audric Lebovitz. submitted (2023). |
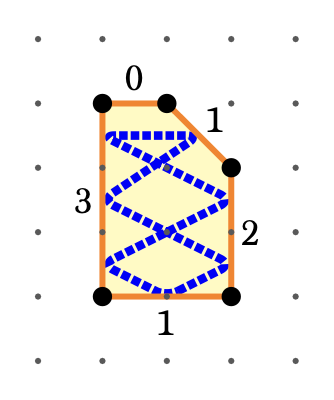 |
|
|
pdf
arxiv |
Minimal degree fibrations in curves and the asymptotic degree of irrationality of divisors,
joint with Jake Levinson and Brooke Ullery. submitted (2023). |
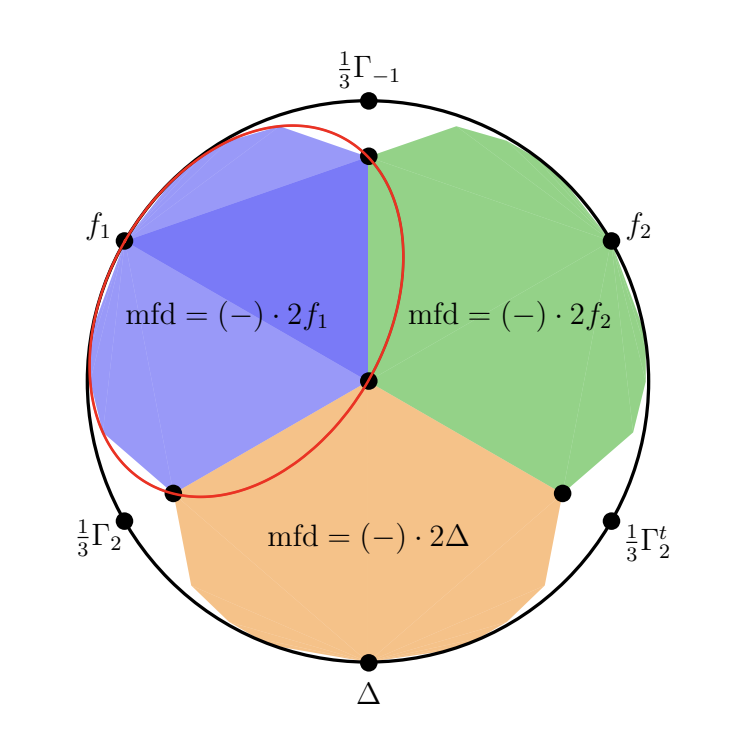 |
|
|
pdf
arxiv |
Smooth limits of plane curves of prime degree and Markov numbers,
joint with Kristin DeVleming. submitted (2022). |
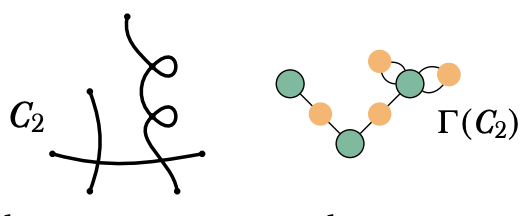 |
|
|
pdf
arxiv |
Fano hypersurfaces with no finite order birational automorphisms,
joint with Nathan Chen and Lena Ji. submitted (2022). |
 |
|
|
pdf
arxiv |
Higher index Fano varieties with finitely many birational automorphisms,
joint with Nathan Chen. Compositio (2022). |
||
|
pdf
arxiv |
Rational endomorphisms of Fano hypersurfaces,
joint with Nathan Chen. accepted at Selecta (2023). |
||
|
pdf
arxiv |
A direct proof that toric rank 2 bundles on projective space split.
Mathematica Scandinavica (2020). |
||
|
pdf
arxiv |
Maximal Chow constant and cohomologically constant fibrations,
joint with Kristin DeVleming. Commun. in Contemporary Math. (2020). |
||
|
pdf
arxiv |
Fano hypersurfaces with arbitrarily large degrees of irrationality,
joint with Nathan Chen. Forum of Math., Sigma (2020). |
 |
|
|
pdf
arxiv |
The degree of irrationality of hypersurfaces in various Fano varieties,
joint with Brooke Ullery. Manuscripta Mathematica (2019). |
||
|
The degree of irrationality of very general hypersurfaces in some homogeneous spaces.
PhD thesis, Stony Brook Univ. (2017). |
|||
|
pdf
arxiv |
The tangent space of the punctual Hilbert scheme,
joint with Dori Bejleri. Mich. Math Journal (2017). |
 |
|
|
pdf
arxiv |
Geometry and stability of tautological bundles on Hilbert schemes of points.
Algebra and Number Theory (2016). |
||