Sandra Lach Arlinghaus

    The Four Color Problem has a rich history.  Readers interested in the history might wish to read appropriate selections in The World of Mathematics.  Here, it is simply stated as a theorem and then animated on a U.S. states map.

The Four Color Theorem.

In the plane, four colors are sufficient to color any map and necessary to color some.

Note:  adjacent regions are to be colored different colors.  States that touch at a point only are not considered to be adjacent.

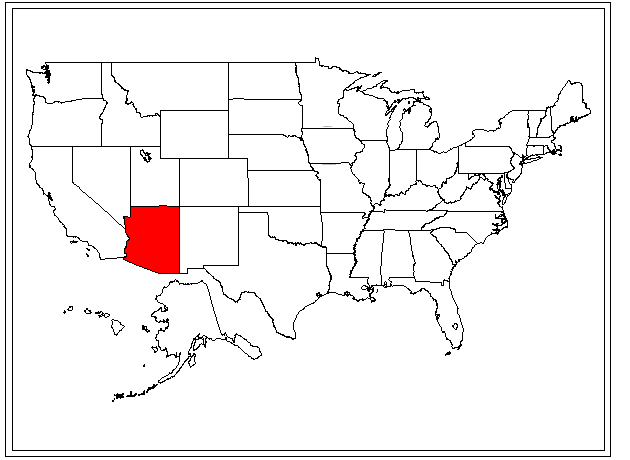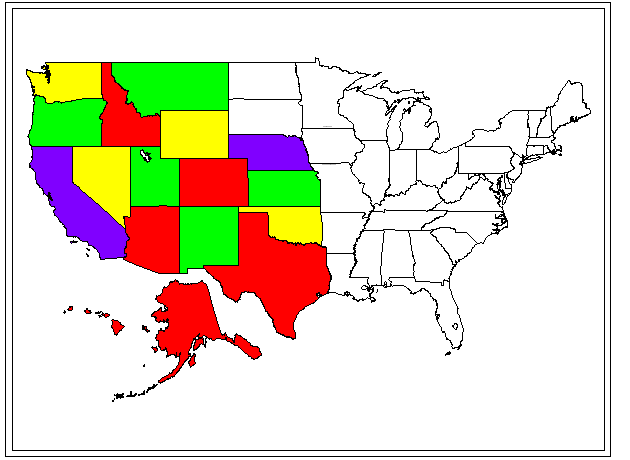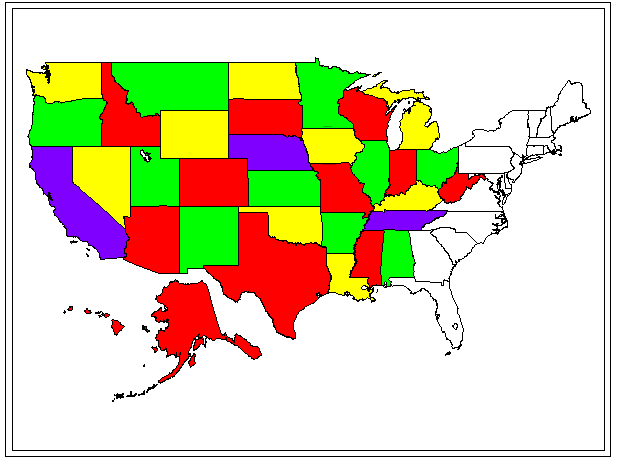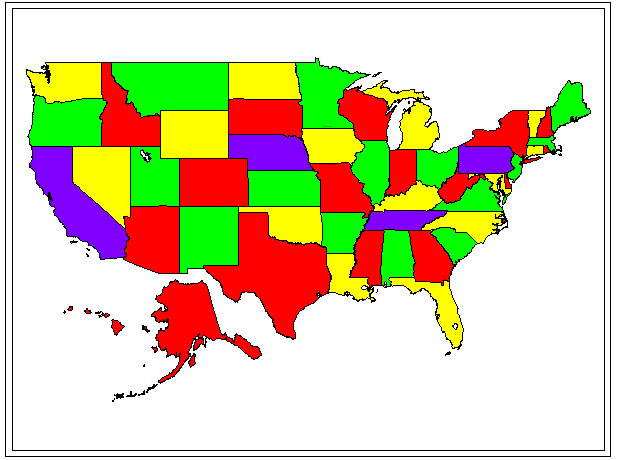
In the coloring scheme below, red was generally used as first choice, green as second, yellow as third, and purple as fourth.  The second, third, and fourth choices were used only when required.

On occasion, the general strategy was violated in order to color efficiently; for example, Montana was colored green so that Idaho could be colored red in a vertical alternation pattern of red/green/red.  The coloring is not unique.  Indeed, one can make inefficient choices so that it appears that one "needs" a fifth color.  The ambitious reader might try to improve upon the scheme here. However, there is always a four (or fewer) color solution available although it may not be easy to find.  Surprisingly, the solution to coloring requirements on surfaces other the plane were determined well ahead of the solution in the plane.
     Thus, it seems suitable that desktop GIS packages should default to four color categories when making thematic maps.  Some software does and some does not.

References

Appel, K. and Haken, W.  A proof of the 4-color theorem.  Discrete Mathematics, 16, 1976, no. 2 (and related references found therein).

Newman, James R., Ed.  The World of Mathematics (in four volumes).  New York:  Random House, 1956.  See especially the chapter entitled "Topology" by R. Courant and H. Robbins.