A GRAPH THEORETIC VIEW OF THE JOIN-COUNT STATISTIC
SANDRA L. ARLINGHAUS AND WILLIAM C. ARLINGHAUS
E-mail to authors:
sarhaus@umich.edu
arlinghaus@ltu.edu
Spatial autocorrelation measures, to some extent, the influence of neighboring regions on each other. Given a thematic map, with regions colored by some variable, two regions are defined to be adjacent (neighbors) if they have a common boundary that includes a line segment (touching at a point, only, does not constitute adjacency). With positive spatial autocorrelation, similar values of the variable are clustered in space. With negative spatial autocorrelation, dissimilar values of the variable are clustered in space. No spatial autocorrelation indicates a random pattern of clustering in space.
How to set bounds for "positive", "negative", and "no" spatial autocorrelation is a problem with an infinite number of solutions. One way, the join-count statistic, is through analogy with simple biological patterns of "pure" and "hybrid" inheritance patterns. Often the biological model is explained using eye-color. Instead, suppose that one mapped variable is "urban". Suppose there are two possible values for this variable…urban, and non-urban (called rural). Represent one state as U and the other as R. Then there are four possible adjacency patterns for any pair of adjacent parcels: UU, UR, RU, and RR. At random, each of these occurs 25% of the time. Thus, pairs of parcels of dissimilar character would be expected 50% of the time. When UR+RU<50%, it follows that values for UU and RR are higher than expected; a condition of positive spatial autocorrelation. When the values are about as expected, the pattern is random. When UR+RU>50%, spatial autocorrelation is negative; dissimilar pairs of parcels dominate (Vasiliev, in CRC Practical Handbook of Spatial Statistics).
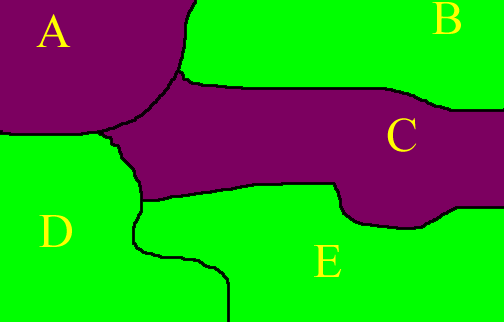
In the map of a hypothetical region below, there are 5 states. The ones of largely urban character are colored purple; rural ones are colored green. The name of each state (A, B, C, D, or E) is inserted as a label. We offer a method of looking a clustering that uses graph theoretic ideas.

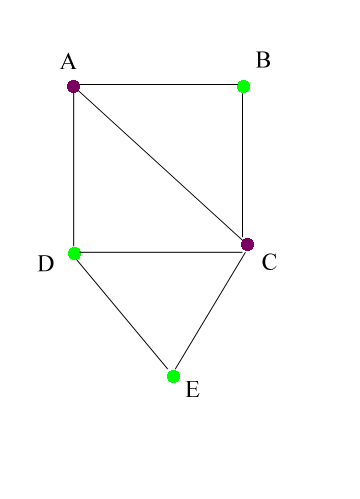
Any spatial object composed of areas and linkages between areas can
be represented as a graph: nodes and edges linking nodes. When
the areas are colored, the corresponding nodes can also be colored to represent
the map coloring. The map above can therefore be represented as a
graph with colored nodes as below. Two nodes have an edge linking
them if and only if the nodes represent adjacent areas on the map.
Thus, A is adjacent to B, C, and D in the map, but not to E; in the graph
there are edges linking A to each of B, C, and D, but not to E.
Enumeration of linkage patterns of colored nodes is tracked quite simply
using an adjacency matrix. The nodes are lined up in any order along
the top and the left-hand side (for example) of a matrix. A value
of 0 in the AC position indicates that there is no link between nodes A
and C; that these nodes do not represent adjacent areas on the map.
A value of 1 in the AC position would indicate that there is a link between
A and C; that these nodes do represent adjacent areas on the map.
Thus, one might choose to merely arrange the labels for the areas in alphabetical
order. The colors behind the node labels represent the node colors.
The colors behind the numerals indicate what sort of adjacency pair that
numeral represents: a light purple background indicates a urban/urban
pairing; a light green background a rural/rural pairing; and, a white background
a rural/urban or a urban/rural pairing. In that case, the following
adjacency matrix emerges:
| A | B | C | D | E | |
| A | 0 | 1 | 1 | 1 | 0 |
| B | 1 | 0 | 1 | 0 | 0 |
| C | 1 | 1 | 0 | 1 | 1 |
| D | 1 | 0 | 1 | 0 | 1 |
| E | 0 | 0 | 1 | 1 | 0 |
However, we do have the freedom to choose other orderings for the labels
without altering any of the results. This particular ordering, based
on alphabetical order of place names, does not lend any additional insight.
It is useful to choose an ordering that does so. If instead, one
orders the place names into two groupings, rural and urban, then the resulting
matrix is partitioned into sets of 0s and 1s in which the size of the "pure"
and "hybrid" adjacency patterns can be read directly from the matrix.
Clustering rows and columns in the matrix reflects corresponding clustering
in the map, as below. Both matrices are symmetric about the main
diagonal and both matrices have 0s all along the main diagonal; in
addition, the rural and urban blocks of submatrices are clustered together
along the main diagonal in the matrix below. In the matrix above,
they are not. Spatial autocorrelation with adjacency matrices is
useful in displaying spatial autocorrelation in the associated map from
which the adjacency matrix was derived. Order of labels can be critical.
| A | C | B | D | E | |
| A | 0 | 1 | 1 | 1 | 0 |
| C | 1 | 0 | 1 | 1 | 1 |
| B | 1 | 1 | 0 | 0 | 0 |
| D | 1 | 1 | 0 | 0 | 1 |
| E | 0 | 1 | 0 | 1 | 0 |
From the matrix below, it is easy to read off that of the 14 cells in which there is an edge (of the 14 pairs of adjacent regions)
UU=2
UR=5
RU=5
RR=2
so that RU+UR>14/2
and autocorrelation is negative; dissimilar regions are clustered.
Directions for further research are suggested by the cleanly-colored adjacency matrix sorted into blocks that mesh with the basic problem structure:
Arlinghaus, S.; Griffith D.; Arlinghaus, W., Drake, W., Nystuen, J. CRC Practical Handbook of Spatial Statistics. 1996. CRC Press.